Статья посвящена рассмотрению некоторых свойств дельта-функции и теорию Дирака. А также приведены несколько примеров по применению этой функций к механическим физическим задачам.
Ключевые слова: классическая теория, элементарная частица, античастица, вспомогательная функция, стержень с переменной сечением, обобщенная функция плотности, центр тяжести, уравнения движения
Article is devoted consideration of some properties ![]() - function and the theory of Dirak. And also on application of this of functions some examples are resulted in mechanical physical problems.
- function and the theory of Dirak. And also on application of this of functions some examples are resulted in mechanical physical problems.
Keywords: the classical theory, an elementary particle, an antiparticle, auxiliary function, a core from a variable the section, the generalised function of density, the centre of gravity, the movement equations
Введение. Как известно, первая элементарная частица — электрон был открыт английским физиком Дж. Дж. Томсоном в 1897 году. С тех пор прошло почти 120 лет [1, 2].
В классической электронной теории (П. К. Друде, Г. А. Лоренц, Дж.Дж. Томсон) принималось что таким механизмом являются неупругие соударения электронов с ионами атома кристаллической решётки твёрдых тел. В отличии от классической теории Поль Дирак создал свою теорию и применил к этой теории ![]() - функцию.
- функцию.
Определение дельта-функции. Поль Адриен Морис Дирак — крупнейший английский физик-теоретик — прославился в 1929 году. Он строил такую теорию, которая описывала бы движение электронов в электрических и магнитных полях с любой скоростью, вплоть до скорости, близкой к скорости света [3]. Речь идёт о квантовой теории, которая объясняет также тот факт, что в атоме электроны могут двигаться только по определенным орбитам, с определёнными значениями энергии. Дирак знал, что электрон обладает определённым моментом вращения, т. е. подобен вращающемуся волчку, и учитывал это при создании своей теории. Когда же теория была им создана, оказалось, что из неё следует ещё и вывод, не предусмотренный Дираком: возможно существование частиц с такой же массой, как электроны, но с противоположным (положительным) знаком заряда. В течение двух лет считали, что теория Дирака хороша для описания движения электрона, а вывод о частицах с положительным зарядом ошибочен, и когда от него удаётся избавиться, теория станет отличной.
Но в 1932 году частицы с положительным зарядом — позитроны, или, как их ещё называют, античастицы электрона, были открыты. Их появление в теории из недостатка превратилось в триумф, в главное достижение теории: открытие Дирака было первым примером появления новых частиц «на острие пера теоретика». Этот пример поучителен с точки зрения взаимоотношений опыта и теории: теория основывается на определённых данных опыта, но последовательное логическое и математическое развитие теории выводит за пределы того материала, который был положен в её основу, приводит к новым предсказаниям.
Дирак является не только одним из лучших физиков — теоретиков нашей планеты, но и замечательным математиком. В своём классическом труде «Основы квантовой механики» Дирак ввёл и широко использовал новую функцию, которой он дал обозначение ![]() : читается «дельта-функция» или «дельта-функция Дирака».
: читается «дельта-функция» или «дельта-функция Дирака».
Дельта функция определяется следующим образом: ![]() при любом
при любом ![]() , т. е. при х<0 и при х>0. При х=0,
, т. е. при х<0 и при х>0. При х=0, ![]() . Кроме того, задаётся условие
. Кроме того, задаётся условие
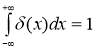 (1)
(1)
Наглядно можно представить себе график функции, похожая на ![]() , как показано на рис. 1.
, как показано на рис. 1.
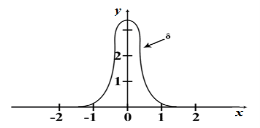
Рис. 1. График функции, похожей на ![]()
Чем более узкой мы сделаем полоску между левой и правой ветвью, тем выше должна быть эта полоска, для того чтобы площадь полоски (т. е. интеграл) сохраняла свое заданное значение, равное 1. При сужении полоски мы приближаемся к выполнению условия ![]() при
при ![]() .
.
Важнейшая формула интеграла с ![]() имеет вид
имеет вид
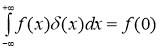 (2)
(2)
В самом деле, так как ![]() при
при ![]() , то значение интеграла не зависит от значений
, то значение интеграла не зависит от значений ![]() ни при каком
ни при каком ![]() . Существенно только значение
. Существенно только значение ![]() там, где
там, где ![]() , т. е. при x. Значит, в той узкой области, где
, т. е. при x. Значит, в той узкой области, где ![]() ,
, ![]() умножается на
умножается на ![]() . Следовательно, из условия (1) получается формула (2). Все эти рассуждения можно провести в обратном порядке, т. е. можно сказать, что
. Следовательно, из условия (1) получается формула (2). Все эти рассуждения можно провести в обратном порядке, т. е. можно сказать, что ![]() есть такая функция, для которой при любом виде вспомогательной функции
есть такая функция, для которой при любом виде вспомогательной функции ![]() имеет место формула (2). Это одно условие приводит ко всем заключениям о виде
имеет место формула (2). Это одно условие приводит ко всем заключениям о виде ![]() , которые были раньше использованы для ее определения. Из формулы (2) следует и то, что
, которые были раньше использованы для ее определения. Из формулы (2) следует и то, что ![]() при
при ![]() , и то, что
, и то, что ![]() , и то, что
, и то, что ![]() .
.
Применения дельта-функции кфизическим задачам. Рассмотрим стержень переменного сечения, к которому прикреплено несколько отдельных точечных грузов (рис. 2). Пусть масса, приходящаяся на единицу длины стержня, выражается функцией ![]() . Масса всего стержня без грузов равна
. Масса всего стержня без грузов равна 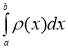 , а вместе с грузами
, а вместе с грузами 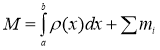 .
.
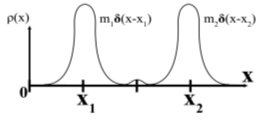
Рис. 2. Отдельные точечные грузы, прикреплённые к стержень
С учетом выше приведенных положение центра тяжести определяется формулой 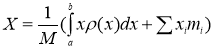 , а момент инерции относительно начала координат определяется как,
, а момент инерции относительно начала координат определяется как, ![]() .
.
Но с помощью дельта-функции можно включить отдельные массы в обобщенную функцию плотности. Обозначим новую функцию ![]() . Она выражается формулой
. Она выражается формулой
![]() (3)
(3)
В самом деле, рассматривая общее распределение массы по стержню, можно сказать, что в тех точках, где находятся грузы, плотность имеет бесконечные подскоки. С помощью новой функции все величины записываются единообразно и более кратко:
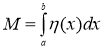 ,
, 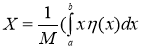 . (4)
. (4)
Понятие дельта-функции позволяет объединит непрерывно распределенные в точечные массы в одном общем выражении.
Другой пример применения дельта — функции относится, к движению материальной точки. Напомним основное уравнение (2 — закон Ньютона)
![]()
Под влиянием удара возникает короткий импульс силы. С другой стороны, действие импульса силы не зависит от закона изменения силы, если только сила достаточно кратковременна. Эти соображения приводят к тому, что дельта-функцию можно построить из различных функций ![]() , об условиях, когда можно конечную функцию
, об условиях, когда можно конечную функцию ![]() заменять обобщенной, особенной функцией
заменять обобщенной, особенной функцией ![]() .
.
Если конкретная форма функции силы несущественна в задаче об ударе, это значит, что ![]() можно поменят на дельта-функцию
можно поменят на дельта-функцию ![]() , где
, где ![]() — момент удара, а
— момент удара, а ![]() — импульс силы. Проведем формально по всем правилам интегрирование уравнения движения под действием единичной дельта-силы. Пусть до удара частица покоилась в начале координат:
— импульс силы. Проведем формально по всем правилам интегрирование уравнения движения под действием единичной дельта-силы. Пусть до удара частица покоилась в начале координат: ![]() ,
, ![]() ,
, ![]() . Уравнение имеет вид
. Уравнение имеет вид ![]() .
.
Интегрируя, получим 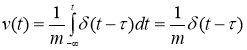 .
.
Скорость выражается ступенчатой функцией времени (рис. 3):
![]() ,
, ![]() ,
, ![]() . Следующей шаг заключается в определении пути. Из
. Следующей шаг заключается в определении пути. Из ![]() получим ответ
получим ответ ![]() ,
, 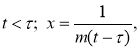
![]() .
.
График пути представлен на соседнем рис. 4.
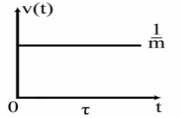
Рис. 3. График скорости
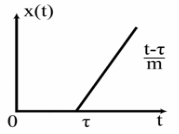
Рис. 4. График пути
Для графика пути ![]() характерен излом в точке
характерен излом в точке ![]() . Здесь ещё раз убеждаемся в том, что вторая производная функции, имеющей излом, содержит дельта-функцию: функция
. Здесь ещё раз убеждаемся в том, что вторая производная функции, имеющей излом, содержит дельта-функцию: функция ![]() имеет излом; согласно уравнению движения сила пропорциональна
имеет излом; согласно уравнению движения сила пропорциональна ![]() ,
, ![]() с изломом получено как раз, при силе пропорциональной
с изломом получено как раз, при силе пропорциональной ![]() , так что при наличии излома
, так что при наличии излома ![]() содержит
содержит ![]() , что и требовалось доказать.
, что и требовалось доказать.
Теперь сделаем следующий шаг. Задача о движении тела под действием заданной силы линейна. Это значит, что если есть два решения ![]() и
и ![]() под действием двух разных сил
под действием двух разных сил ![]() и
и ![]() , то сумма решений
, то сумма решений ![]() является решением, соответствующим действию суммы сил
является решением, соответствующим действию суммы сил ![]() . Такое свойство есть следствие того просто факта, что вторая производная суммы функцией есть каждой функции. Принимая во внимание
. Такое свойство есть следствие того просто факта, что вторая производная суммы функцией есть каждой функции. Принимая во внимание ![]()
![]() получим
получим ![]() что и требовалось — сумма решений
что и требовалось — сумма решений ![]() описывает движение под действием суммы сил.
описывает движение под действием суммы сил.
Заключение. Нужно сделать только одну оговорку: решения уравнения движения зависят не только от закона силы, но и от начальных условий, т. е. начального положения и начальной скорости рассматриваемой массы. Если мы выберем эти условия так: ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() , то и сумма решений будет удовлетворить тому же условию
, то и сумма решений будет удовлетворить тому же условию ![]() ,
, ![]() ,
, ![]() .
.
Такой способ получения решения имеет очень большое общее значение. Резюмируем: если для линейной системы известно решение, относящееся к воздействию дельта-функции (![]() в примере), получается простым суммированием или интегрированием.
в примере), получается простым суммированием или интегрированием.
Литература:
- Мухин К. Н. Занимательная ядерная физика. — М.: Атомиздат, 1969. — 145 с.
- Бекжонов Р. Б. Элементарная ядерная физика. — T.: Учитель, 1982. — 407 с (на узбекском языке).
- Т. М. Муминов, А. Б. Холикулов, Ш. X. Xушмуродов. Физика атомного ядра и частиц. — T.: НОФУ. 2009. -487 с (на узбекском языке).

