Стохастические исчисления — это один из тех великолепных разделов математики. Теория стохастического интегрирования начиналась с интегрирования по броуновскому движению. Ито в 40-х гг. прошлого века вывел правила действий со стохастическими интегралами и знаменитую «формулу Ито». Но в этой статье мы научимся вычислять стохастические интегралы по определению.
Ключевые слова : стохастический интеграл, минимальная сигма-алгебра, математическое ожидание, неупреждающая функция, дисперсия, винеровский процесс, броуновское движение, борелевское множество, ступенчатые функции.
Keywords : stochastic integral, minimal sigma algebra, mathematical expectation, non-preemptive functions, dispersion, Wiener process, Brownian motion, Borel set, step functions.
Введем понятие стохастического интеграла от случайного процесса по винеровскому процессу
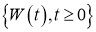
Далее нам пригодится обозначение
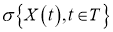
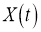
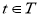
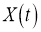
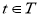
Определение.
Случайная функция
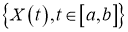
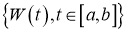
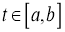
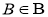
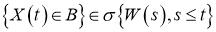
Если говорить очень грубо, то это значит, что события, связанные с процессом
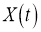
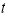
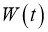
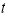
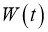
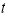
Как обычно в теории меры, интеграл от случайной функции мы построим как предел интеграла от простых (ступенчатых, кусочно-постоянных) функций. Предел этот будем мы будем понимать в среднем квадратичном смысле. Под интегралом же простой функции
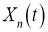
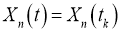
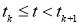
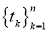
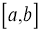
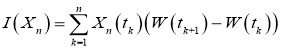
Теорема.
Пусть
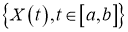
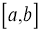
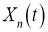
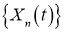
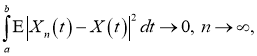
и для которой существует средний квадратичной предел
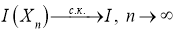
Определение.
Предел
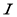
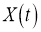
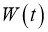
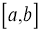
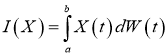
Если сравнить это определение с интегралом от неслучайной функции по случайному процессу, то можно видеть, что все отличие состоит в паре формальностей: вместо непрерывной подынтегральной функции мы имеем дело с средним квадратичным непрерывной функцией и дополнительно требуем от нее свойство неупреждаемости. Можно доказать, что значение
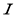
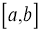
Еще нам понадобится следующая лемма.
Лемма.
Пусть
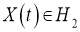
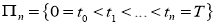
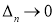
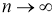
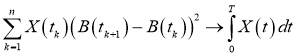
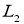
где,
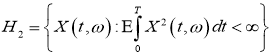
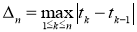
Пример 1. Вычислить стохастический интеграл
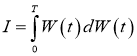
Решение.
Подынтегральная функция
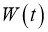
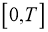
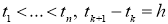
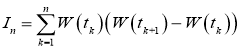
Для краткости обозначений введем
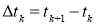
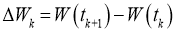
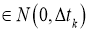
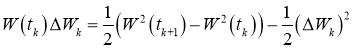
Отсюда следует, что
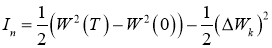
Первое слагаемое этого выражения не зависит от
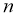
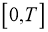
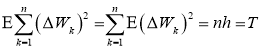
и дисперсию
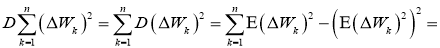
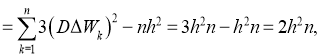
где для расчета момента четвертого порядка можно воспользоваться теоремой Вика. Получается, что
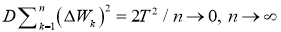
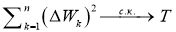
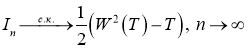
поэтому окончательно заключаем, что
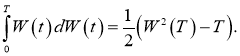
Пример 2
. Пусть
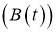
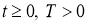
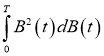
Решение.
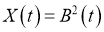
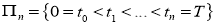
такую, что
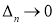
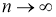
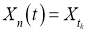
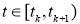
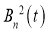
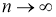
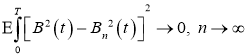
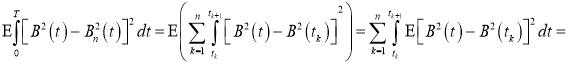

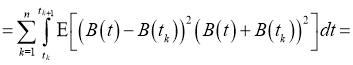
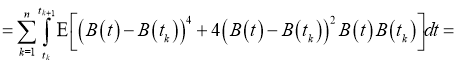
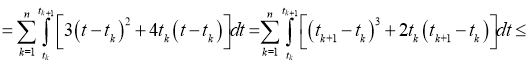
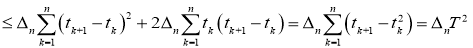
Так как
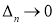
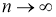
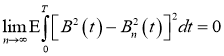
Здесь
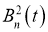
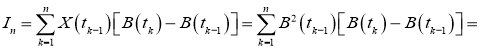
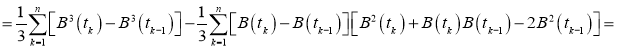
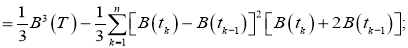
Исходя из леммы, следующие сходимость будет правильной:
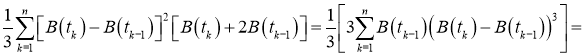
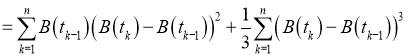
Для первой и второй частей суммы выполняется Лемма. То есть,
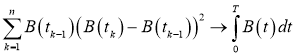
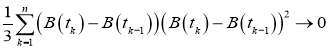
Тогда ответ таков:
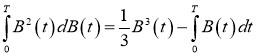
Литература:
- Гасников А. В., Горбунов Э. А., Гуз С. А., Лекции по случайным процессам. — М, 2019.
- Оксандель Б., Стохастические дифференциальные уравнения. — М, 2003.

