Пусть 
— некоторая аналитическая функция на 
. Определим регулярную функцию
.
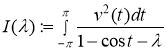Задача состоит из определения функции 
в точках 
и 
. Обычно такие задачи возникают при изучении пороговых явлений в спектре модели Фридрихса и их обобщений [1].
Очевидно, что
,
.
Из определения функции видно, что оно монотонно возрастает в интервалах 
и 
. Из теоремы о предельном переходе под знаком интеграла Лебега [2] следует, что существуют конечные или бесконечные интегралы
,
.
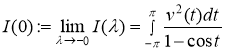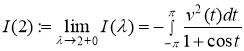Для любого 
и 
положим
.
Тогда имеет место соотношение
.
Отметим, что если 
, то из аналитичности функции 
в 
следует, что существуют положительные числа 
и 
такие, что имеет место неравенство
(1)
для некоторого 
. В силу непрерывности функции 
на компактном множестве 
, существует число 
такое, что имеет место неравенство
(2)
при всех 
. Так как функция 
имеет невырожденный минимум в точке 
, для найденных положительных и также имеет место неравенства
, (3)
. (4)
Для определенности предположим, что 
. Тогда имеет место равенство
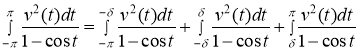. (5)
Учитывая неравенства (2) и (4) для первого и третьего слагаемого стоящей в правой части равенства (5) имеем
,
.
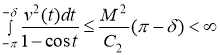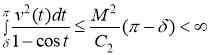Далее, учитывая неравенства (1) и (3), для второго слагаемого стоящей в правой части равенства (5) имеем
.
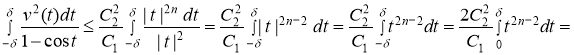
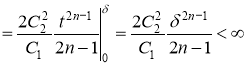Таким образом, если , то
.
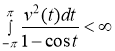Пусть теперь 
. В этом случае силу непрерывности функции 
существуют положительные числа 
и 
такие, что 
при всех 
. Учитывая этот факт и неравенства (3) получим, что
.
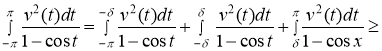
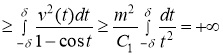Таким образом, в случае имеет место соотношение
.
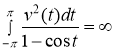Рассуждая аналогично можно указать условия существования интеграла
.
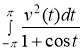Пусть 
– гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на 
. В 
рассмотрим ограниченный самосопряженный модель Фридрихса
.
Для этой модели определитель Фредгольма имеет вид
.
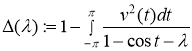Изложенные факты в этой работе играют важную роль при изучении спектральных свойств оператора 
, т. е. модели Фридрихса.
Литература:
- S.Albeverio, S. N. Lakaev, Z. I. Muminov. The threshold effects for a family of Friedrichs model under rank one perturbations. Journal of Mathematical Analysis and Applications. 330 (2007), P. 1152–1168.
- А. Н. Колмогоров, С. В. Фомин. Элементы теории функций и функционального анализа. М. «Наука». 1981.
