Как известно, если скорость изменения состояния системы значительно меньше скорости изменения внешних условий, то процесс является неравновесным.
При фильтрации вязкоупругой жидкости в пористой среде ее внутреннее напряжение стремится к равновесному значению. Характерное время перехода к равновесному состоянию — это время релаксации. В данной статье делается попытка определения времени релаксации при фильтрации жидкости через слабо неоднородную среду, когда поток в целом не равновесен.
Ключевые слова: время релаксации, неравновесность, фильтрация, скорость, проницаемость.
As you know, if the rate of change of the state of the system is much less than the rate of change of external conditions, then the process is nonequilibrium.
When filtering a viscoelastic fluid in a porous medium, its internal stress tends to an equilibrium value. The characteristic transition time to the equilibrium state is the relaxation time. This article attempts to determine the relaxation time during fluid filtration through a slightly inhomogeneous medium, when the flow as a whole is not in equilibrium.
Key words: relaxation time, nonequilibrium, filtration, speed, permeability.
Причины, обусловливающие неравновесность фильтрационных течений, могут иметь различную физико-химическую природу, например явления сорбции и десорбции в пористой среде, фазовые превращения углеводородных систем, состояние газоконденсатных смесей в пористой среде, деформации пород-коллекторов.
Затягивание переходных процессов приводит к неравновесности потока при движении в отдельных порах. Этот тип неравновесности можно наблюдать при стационарном течении тяжелой нефти в капилляре с переменным сечением. В этом случае зависимость «дебит-перепад давления» отклоняется от прямолинейной, что связано с появлением дополнительных сопротивлений, обусловленных релаксационными свойствами нефти. При движении вязкоупругой нефти через пористую среду, представляющую собой сложную систему каналов нерегулярной формы, возникают упругие напряжения, приводящие к увеличению эффективной вязкости. В этом случае при одной и той же скорости движения эффективная вязкость нефти возрастает с уменьшением проницаемости пористой среды.
Наличие у жидкости релаксационных свойств определяет характер сопротивления при движении в пористой среде. Поскольку релаксирующая жидкость реагирует на изменение условий с некоторым запаздыванием, то в зависимости от скорости движения характер сопротивления будет изменяться. Когда течение достаточно медленное, соответственно медленно происходит деформация жидких частичек, и жидкость успевает «реагировать» на эти изменения. С увеличением скорости движения время прохождения через сужения уменьшается, и жидкие частицы не успевают деформироваться, т. е. время релаксации уменьшается. Это приводит к увеличению сопротивления движения. В связи с вышесказанным определение времени релаксации, скорости фильтрации неравновесной жидкости и дебита имеет большое практическое значение, которое и рассматривается в данной статье.
В работе [1] показано, что когда фильтрация жидкости происходит через слабо неоднородную среду, эффективная вязкость зависит от скорости фильтрации. Это связано с неравновесностью потока в целом. Формула для эффективной вязкости имеет вид:
![]() (1)
(1)
где ![]() — вязкость жидкости, замеренная вискозиметром при малых скоростях сдвига;
— вязкость жидкости, замеренная вискозиметром при малых скоростях сдвига; ![]() — скорость фильтрации жидкости;
— скорость фильтрации жидкости; ![]() — время релаксации,
— время релаксации, ![]() и
и ![]() — пористость и проницаемость среды.
— пористость и проницаемость среды.
Учитывая также влияние на время релаксации начального градиента, можно написать следующие формулы:
![]()
откуда
![]() или
или 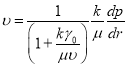 (2)
(2)
где ![]() — начальный градиент.
— начальный градиент.
Далее учитывая неравновесность потока по формуле (1) можно написать следующую формулу:
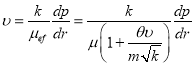 (3)
(3)
Приравнивая правые части формул (2) и (3) можно получить:
Учитывая формулу ![]() получим:
получим: ![]()
или
![]() (5)
(5)
Подставляя в (5) формулу для скорости с учетом влияния начально градиента,
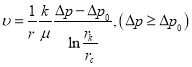 (6)
(6)
после несложных преобразований получаем:
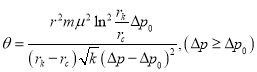 (7)
(7)
где
![]()
Таким образом, в данной статье получена формула для времени релаксации неравновесной жидкости при фильтрации через слабо неоднородную пористую среду с учетом влияния начального градиента.
Литература:
- Ольховская В. А. Подземная гидромеханика. Фильтрация неньютоновской нефти: Учебное пособие. — М.: ОАО «ВНИИОЭНГ», 2011–224 с.
- Подземная гидравлика. Учебник для вузов./ К. С. Басниев, А. М. Власов, И. Н. Кочина, В. М. Максимов. — М.: Недра, 1986–303 с.







