Фильтрование нашло широкое применение во многих отраслях промышленности для сгущения твердой фазы суспензии и осветления жидкостей, в том числе сбросовых вод промышленных предприятий (например, целлюлозно-бумажных, угледобывающих) и коммунального хозяйства. Начало теории фильтрации суспензии связано с [1,2,3].
В [4, 5] предложено, что осадок в пористом пространстве фильтра глобулярной структуры имеет две формы — вымываемую и невымываемую. Соответственно зоны фильтра называются активными и пассивными. Активные зоны, омываемые струйной составляющей потока, формируют вымываемый осадок с концентрацией ![]() , пассивные зоны, являющиеся застойными, формируют невымываемый осадок с концентрацией
, пассивные зоны, являющиеся застойными, формируют невымываемый осадок с концентрацией ![]() . Обозначим полную емкость фильтра через
. Обозначим полную емкость фильтра через ![]() . Из изложенного следуют
. Из изложенного следуют ![]() , где
, где ![]() и
и ![]() — емкости соответственно активных и пассивных зон. Указанные емкости являются динамическими характеристиками. Они зависят не только от «качества» дисперсной фазы, но и от скорости и структуры потока, а также геометрии слоя.
— емкости соответственно активных и пассивных зон. Указанные емкости являются динамическими характеристиками. Они зависят не только от «качества» дисперсной фазы, но и от скорости и структуры потока, а также геометрии слоя.
Кинетика осадка образования в процессе фильтрация суспензии в пористой среде, как правило определяется в виде [6]
![]() ,
,
где, ![]() — концентрация суспензии,
— концентрация суспензии, ![]() – концентрация осадка,
– концентрация осадка, ![]() — функция характеризующая кинетику осадкообразования, зависит от формы глобулярной структуры.
— функция характеризующая кинетику осадкообразования, зависит от формы глобулярной структуры.
Для невымываемого осадкообразования, где взвешенные частицы, когда-то осевшие в поровом объеме, никогда не освобождаются потоком жидкости [1,7], уравнение кинетики осаждения этого типа имеет форму ![]() . Где
. Где![]() не является постоянной в течение процесса фильтрации,
не является постоянной в течение процесса фильтрации, ![]() — скорость фильтрации.
— скорость фильтрации.
Для вымываемого осадкообразования, где взвешенные частицы поочередно осаждаются и освобождаются потоком жидкости [2,8], соответствующее уравнение кинетики имеет вид ![]() , с феноменологическими коэффициентами осаждения и освобождения,
, с феноменологическими коэффициентами осаждения и освобождения,![]() и
и![]() , определяемыми эмпирическим (опытным) путем.
, определяемыми эмпирическим (опытным) путем.
В [4, 5] кинетика образования невымываемой формы осадка описывается уравнением
![]() ,(1)
,(1)
и аналогична моделям безотрывного фильтрования, где ![]() — концентрация суспензии,
— концентрация суспензии,![]() — коэффициент, связанный с эффектом уплотнения (старения) осадка,
— коэффициент, связанный с эффектом уплотнения (старения) осадка,
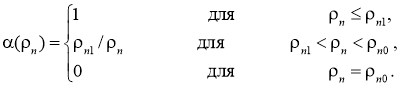 (2)
(2)
Для активных зон в [4, 6] дано уравнение кинетики в виде
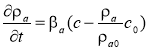 ,(3)
,(3)
где ![]() — постоянная концентрация,
— постоянная концентрация, ![]() — коэффициент, характеризирующий кинетику в активной зоне, совпадающий с линейной моделью фильтрация.
— коэффициент, характеризирующий кинетику в активной зоне, совпадающий с линейной моделью фильтрация.
В [9–10] на основе вероятностного подхода предлагаются модифицированные уравнения кинетики кольматации и суффозии. Кольматационные и суффозионные процессы зависят от градиента давления — ![]() , причем чем больше
, причем чем больше ![]() , тем меньше вероятность кольматации и тем больше вероятность суффозии [9]. Исходя из этого, кинетическое уравнение (3), характеризующее осаждение и освобождение твердых частиц в вымываемой зоне пористой среды можно представить в виде
, тем меньше вероятность кольматации и тем больше вероятность суффозии [9]. Исходя из этого, кинетическое уравнение (3), характеризующее осаждение и освобождение твердых частиц в вымываемой зоне пористой среды можно представить в виде
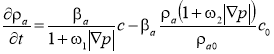 ,(4)
,(4)
где ![]() ,
, ![]() — постоянные коэффициенты,
— постоянные коэффициенты, ![]() — модуль градиента давления.
— модуль градиента давления.
Степень вымываемости осадка характеризует величина ![]() . Экспериментально показано [11], что
. Экспериментально показано [11], что ![]() , причем для тонкодисперсных загрузок (0,05–0,1 мм) при тех же условиях фильтрования
, причем для тонкодисперсных загрузок (0,05–0,1 мм) при тех же условиях фильтрования ![]() меньше, чем для крупнозернистых (0,5–2 мм), а для пористых материалов с развитой поверхностью (керамзит) меньше, чем для материалов с гладкой поверхностью (песок). Это подтверждает, что емкость активной зоны намного меньше, чем емкость пассивной, т. е.
меньше, чем для крупнозернистых (0,5–2 мм), а для пористых материалов с развитой поверхностью (керамзит) меньше, чем для материалов с гладкой поверхностью (песок). Это подтверждает, что емкость активной зоны намного меньше, чем емкость пассивной, т. е. ![]() .
.
Рассмотрим полубесконечный однородный пласт с первоначальной пористостью ![]() , заполненный однородной жидкостью (те жидкостью без дисперсных частиц) В точке
, заполненный однородной жидкостью (те жидкостью без дисперсных частиц) В точке ![]() , начиная с
, начиная с ![]() в пласт поступает суспензия с концентрацией
в пласт поступает суспензия с концентрацией ![]() со скоростью фильтрации
со скоростью фильтрации ![]()
Система уравнений фильтрации суспензии состоит из уравнения баланса с учетом диффузии, модифицированного уравнения кинетики в активной зоне (4), уравнения (1) с учетом явления старения в пассивной зоне и закона Дарси, в одномерном случае имеет вид
![]() ,
,
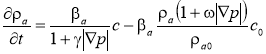 ,(5)
,(5)
![]() ,
,
![]() ,
, ![]() ,
,
где ![]() — текущая пористость среды,
— текущая пористость среды, ![]() — коэффициент фильтрации.
— коэффициент фильтрации.
Для выражения ![]() используем закон Кармана-Козени
используем закон Кармана-Козени ![]() ,
, ![]() .
.
Для замыкания системы (5) используем следующие начальные и граничные условия
![]() .(6)
.(6)
Для решения задачи (5)-(6) применим метод конечных разностей [10]
При фильтрования суспензий образующийся осадок, как правило, является невымываемым [12], поэтому для таких загрузок можно положить ![]() . Тогда система (5) в пренебрежении активной составляющей скорости формирования осадка
. Тогда система (5) в пренебрежении активной составляющей скорости формирования осадка ![]() примет вид
примет вид
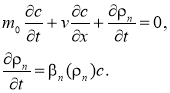 (8)
(8)
Решаем эту систему при условиях
На основе численного решения задач (5)-(6) и (7)-(8) определены поля концентраций ![]() .
.
Из рис. видно, что пренебрежение эффектами вымываемости осадка приводит к увеличению концентраций взвешенных частиц в потоке суспензии и невымываемого осадка в соответствующих точках пласта.
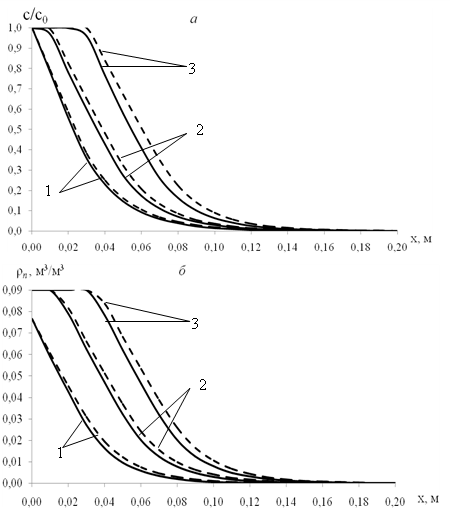
Рис. 1. Профили изменения ![]() (а),
(а), ![]() (б) при (- — -
(б) при (- — - ![]() , ───
, ─── ![]() , 1 — t=450 c, 2 — t=900 c, 3 — t=1350 c)
, 1 — t=450 c, 2 — t=900 c, 3 — t=1350 c) ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() м/c,
м/c, ![]() с-1,
с-1, ![]() м/МПа,
м/МПа, ![]() м/МПа,
м/МПа, ![]() м2/(МПа·с)
м2/(МПа·с)
Литература:
- Iwasaki T. Some notes on sand filtration of sand filtration, Journal of American Water Works Assosation 29 (5) (1937) 1591–1602.
- Минц Д. М. Кинетика фильтрации малоконцентрированных водных суспензий на водоочистных фильтрах. — Докл. АН СССР, 1951, 78, № 2, с. 315–318.
- Шехтман Ю. М. Фильтрация малоконцентрированных суспензий. М.: Изд-во АН СССР, 1961. 212 с.
- Веницианов Е. В., Рубинштейн Р. Н. Динамика сорбции из жидких сред. — М.: Наука, 1983. — 237 с.
- Веницианов Е. В., Сенявин М. М. Математическое описание фильтрационного осветления суспензий // Теорет. основы хим. технологии, 1976. 10, № 4. С. 584–591.
- C. Tien, B. V. Ramarao, Granular Filtration of Aerosols and Hydrosols, 2nd ed., Elsevier, 2007
- Ives K. J., Theory of filtration. Special Lecture No.7, in: Proceedings of the International Water Supply Association, Eight Congress, Vienna, 1969, vol. 1, pp. K3-K28.
- Adin A., Rebhun M., A model to predict concentration and head-loss profiles in filtration // Journal of American Water Works Association 69 (8) (1977) 444–453.
- Хужаёров Б Х Модель фильтрации суспензии с учетом кольматации и суффозии // ИФЖ. 1992. Т. 63, № 1 С 72–79
- Хужаёров БХ, Давиденко МА О модификации модели кольматационно-суффозионной фильтрации // ДАН РУз. 1997. № 5 С 25–28
- Митин Б. А. Исследование влияния структурно-механических свойств осадка на работу зернистых осветлительных фильтров: Автореф. дис. канд. техн. наук М.: ВНИИ ВОДГЕО, 1969, — 18 с.
- Скворцов Н.Г, Веницианов Е. В., Сенявин М. М. Расчет фильтрационного осветления малоконцентрированных суспензий на тонкодисперсных загрузках. — Теорет. основы хим. технологии, 1981, 15, № 1, с. 141–144.







