Пусть ![]() — трехмерный тор, т. е. трехмерный куб с соответствующим отождествлением противоположных граней. Всюду в работе
— трехмерный тор, т. е. трехмерный куб с соответствующим отождествлением противоположных граней. Всюду в работе ![]() рассматривается как абелева группа, в которой операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в
рассматривается как абелева группа, в которой операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в ![]() по модулю
по модулю ![]() . Например, если
. Например, если
![]()
![]() ,
,
то
![]()
![]() .
.
Рассмотрим функцию многих переменных следующего вида
![]() ,
,
где ![]() . Здесь,
. Здесь, ![]() — некоторое натуральное число.
— некоторое натуральное число.
Простые вычисления показывают, что
![]() ;
;
![]()
![]() .
.
Теперь изучаем точки невырожденного минимума функции ![]() .
.
Случай 1. Пусть ![]() . Тогда функция
. Тогда функция ![]() имеет единственный невырожденный минимум в точке
имеет единственный невырожденный минимум в точке ![]() . Действительно, в этом случае
. Действительно, в этом случае
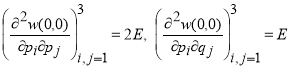 ,
,
где ![]() единичная матрица размера
единичная матрица размера ![]() . Поэтому для функции
. Поэтому для функции ![]() , где
, где
![]() ,
,
![]()
имеет место равенство
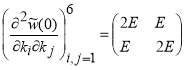 .
.
Очевидно, что последняя матрица положительна определенная, и следовательно, функция ![]() имеет единственный невырожденный минимум в точке
имеет единственный невырожденный минимум в точке ![]() .
.
Случай 2. Пусть
![]()
![]() .
.
В данном случае функция ![]() имеет совпадающий невырожденный минимум в точках
имеет совпадающий невырожденный минимум в точках ![]() ,
, ![]() и имеет место соотношениt
и имеет место соотношениt
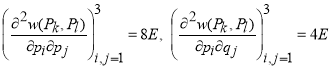 ,
, ![]() .
.
Следовательно,
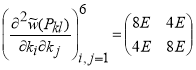 ,
, ![]() .
.
Так как последняя матрица положительно определенная, и следовательно, функция ![]() имеет невырожденный минимум в точках
имеет невырожденный минимум в точках ![]() ,
, ![]() .
.
Случай 3. Пусть ![]() . Введем следующие точки из
. Введем следующие точки из ![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В данном случае функция ![]() имеет совпадающий невырожденный минимум в точках
имеет совпадающий невырожденный минимум в точках ![]() ,
, ![]() и имеет место соотношение
и имеет место соотношение
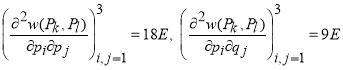 ,
, ![]() .
.
Следовательно, функция ![]() имеет невырожденный минимум в точках
имеет невырожденный минимум в точках ![]() ,
, ![]() .
.
Теперь остановимся коротко на применениях. Случай ![]() обсуждался в работе [1], где изучено существование эффекта Ефимова для матричных операторов. Случай
обсуждался в работе [1], где изучено существование эффекта Ефимова для матричных операторов. Случай ![]() обсуждался в работе [2], где доказана бесконечность числа собственных значений, лежащих в лакунах существенного спектра одного матричного оператора размера
обсуждался в работе [2], где доказана бесконечность числа собственных значений, лежащих в лакунах существенного спектра одного матричного оператора размера ![]() . Случай
. Случай ![]() обсуждался в работе [3]. Там показано существование бесконечного числа собственных значений, лежащих в существенном спектре одного матричного оператора размера
обсуждался в работе [3]. Там показано существование бесконечного числа собственных значений, лежащих в существенном спектре одного матричного оператора размера ![]() . Случай произвольного
. Случай произвольного ![]() обсуждался в работах [4] и [5], где получена асимптотика дискретного спектра трехчастичного модельного оператора и для матричного оператора размера
обсуждался в работах [4] и [5], где получена асимптотика дискретного спектра трехчастичного модельного оператора и для матричного оператора размера ![]() , соответственно.
, соответственно.
Литература:
- S.Albeverio, S. N. Lakaev, T. H. Rasulov. The Efimov Effect for a Model Operator Associated with the Hamiltonian of non Conserved Number of Particles. Methods of Functional Analysis and Topology. 13:1 (2007), P. 1–16.
-
M. I. Muminov, T. H. Rasulov. On the eigenvalues of a
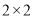 block operator matrix. Opuscula Mathematica, 35:3 (2015), P. 371–395.
block operator matrix. Opuscula Mathematica, 35:3 (2015), P. 371–395.
- M. I. Muminov, T. H. Rasulov. Embedded eigenvalues of an Hamiltonian in bosonic Fock space. Communications in Mathematical Analysis. 17:1 (2014), P. 1–22.
- Т. Х. Расулов. Асимптотика дискретного спектра одного модельного оператора, ассоциированного с системой трех частиц на решетке. Теоретическая и математическая физика. 163:1 (2010), С. 34–44.
- Т. Х. Расулов. О числе собственных значений одного матричного оператора. Сибирский математический журнал. 52:2 (2011), С. 400–415.







