Некоторые задачи физики твердого тела [1], квантовой теории поля [2] и статистической физики [3] приводят к необходимости исследования резонансов и собственных значений обобщенной модели Фридрихса.
В настоящей работе рассматривается семейство обобщенных моделей Фридрихса 
,
. Рассмотрим случай, когда параметр функция 
(см. ниже) имеет специальный вид и имеет невырожденный минимум в 
, 
в различных точках шестимерного тора 
.
Пусть 
— трехмерный куб с соответствующим отождествлением противоположных граней. Всюду в работе 
рассматривается как абелева группа, в которой операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в 
по модулю 
. Пусть 
— одномерное комплексное пространство, 
- гильбертово пространство квадратично интегрируемых (комплекснозначных) функций, определенных на .
Обозначим через 
прямую сумму пространств 
и 
, т. е. 
. Гильбертово пространство называется двухчастичная обрезанная подпространства Фоковского пространства.
Рассмотрим семейство обобщенных моделей Фридрихса , действующих в гильбертовом пространстве и задающийся как операторная матрица
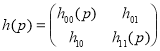(1)
где операторы 
, 
, 
и 
, 
определяются по формулам
, 
,
, 
.
Здесь
, 
-вещественнозначная непрерывная (ненулевая) функция на , а функции 
и 
имеют вид 
, 
, где 
функция 
определяется с помощью равенства
, 
,
а 
натуральное число. Здесь и в дальнейшем интеграл без указания пределов всюду означает интегрирование по всей области изменения переменных интегрирования.
Легко можно проверить, что в этих предположениях оператор , , определенный по формуле (1) и действующий в гильбертовом пространстве 
, является ограниченным и самосопряженным.
Пусть оператор 
, действует в 
как
.
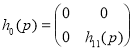Оператор возмущения 
, оператора , является самосопряженным оператором ранга 2. Следовательно, из известной теоремы Г.Вейля о сохранении существенного спектра при возмущениях конечнего ранга вытекает, что существенный спектр оператора , совпадает с существенным спектром оператора , . Известно, что 
, где числа 
и 
определяются равенствами
, ,
, .
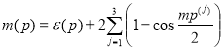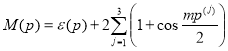Из последних двух фактов следует, что
. (2)
Замечание 1.Отметим, что существенный спектр оператора
, 
совпадает с точкой 
и следовательно, для любого 
мы не можем сказать, что существенный спектр оператора 
является абсолютно непрерывным.
Обозначим через 
число тех точек 
таких, что 
, 
и 
, 
, 
, 
для всех 
, где
Легко можно проверить, что 
и функция 
имеет невырожденный минимум в точках 
, 
.
Дополнительно будем предпологать, что 
Потому что, если 
, тогда 
и в настоящей работе нам интересен случай 
.
Замечание 2. Заметим, что верно равенство 
, 
.
Из определения числа 
и равенства (2) вытекает, что 
. При каждом фиксированном 
определим регулярную в 
функцию (определитель Фредгольма, ассоциированный с оператором , )
.
Далее, везде дополнительно предполагается, что все частные производные первого порядка функции 
непрерывны на 
.
Так как функция 
имеет невырожденный минимум, равный нулю в точках 
, и все частные производные первого порядка функции непрерывны на , существует конечный интеграл
, .
Из теоремы о предельном переходе под знаком интеграла Лебега и равенства
, следует, что
, 
.
Теорема 1.Число 
является собственным значением оператора 
тогда и только тогда, когда 
и 
, .
Литература:
- D. C. Mattis. The few-body problem on a lattice. Rev. ModernPhys., 58 (1986), No. 2, 361–379.
- Фридрихс К. Возмущения спектра операторов в гильбертовом пространстве. М.: Мир.1972.
- Малышев В. А., Минлос Р. А. Кластеpные операторы. Тpуды семинаpа им. И. Г. Петpовского, 1983. Вып. 9. c.63–80.
