Как известно, числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с некоторым числом, называется арифметической прогрессией [1]. А числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на некоторое отличное от нуля постоянное число, называется геометрической прогрессией [1]. Из определения арифметической и геометрической прогрессий мы видим, что они основаны на арифметических действиях суммы (разности) и умножения (деления). Возникает вопрос: существует ли прогрессия, которая основана на действии возведение в степень число. В работе [2] был определен новый вид прогрессии — показательная прогрессия.
Также в работе [2] в качестве характеристического свойства показательной прогрессии рассматривается следующее утверждение. Если 
— показательная прогрессия, то для любого натурального 
выполняется равенство
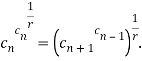
В данном проекте будет доказана другая формула, описывающая характеристическое свойство показательной прогрессии. Также будет рассмотрено неравенство — аналог неравенству Коши [3].
Ключевые слова: числовые последовательности, прогрессия, показательная прогрессия, неравенство Коши.
Докажем следующую теорему, описывающую характеристическое свойство показательной прогрессии.
Теорема 1. Для каждого члена показательной прогрессии, начиная со второго, выполняется равенство:
Доказательство. По определению [2] показательной прогрессии
Отсюда следует, что
т. е.
Преобразуем полученное выражение
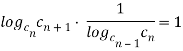
(1)
что и требовалось доказать.
Выразим 
из равенства (1).
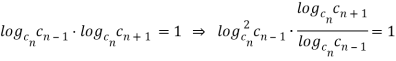
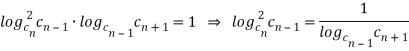
Так как характеристическое свойство арифметической прогрессии построено на основе арифметической средней, а геометрическая прогрессия — на основе геометрической средней, то характеристическое свойство показательной прогрессии должно построено на основе какой-то другой числовой средней. В качестве этой средней будем считать последнее из равенств.
Определение 1. Пусть даны два положительных числа 
. Причем эти числа либо больше единицы, либо меньше единицы одновременно. Средним показательным чисел называется величина, определяемая следующим образом:
(2)
Замечание 1. Если заменить местами , значение средней показательной не изменится.
Доказательство. Преобразуем выражение (2) следующим образом:
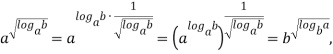
что и требовалось доказать.
Замечание 2. Среднюю показательную можно определить и следующим образом:
где 
— это такое произвольное положительное число, как , одновременно с ними либо больше единицы, либо — меньше.
Доказательство. Преобразуем выражение (2) следующим образом:
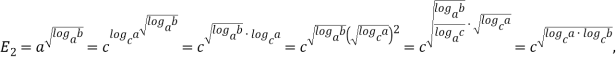
что и требовалось доказать.
Введем обобщенное определение средней показательной для 
чисел.
Определение 2. Пусть даны положительные числа 
и . Причем эти числа либо больше единицы, либо меньше единицы одновременно. Средним показательным чисел называется величина, определяемая следующим образом:
Среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического — это неравенство называется неравенством Коши [3]: если 
, 
, то
В более общем виде: для неотрицательных чисел 
справедливо неравенство между их средним арифметическим и средним геометрическим
причем равенство возможно лишь при условии 
.
Рассмотрим следующую теорему, описывающую связь между неравенством Коши и средним показательным.
Теорема 2. Пусть даны числа 
, каждое из которых больше единицы. Тогда выполняется следующее неравенство:
причем равенство возможно лишь при условии 
Доказательство. Запишем неравенство Коши для чисел 
.
Используя свойства логарифма числа, преобразуем это выражение следующим образом:
что и требовалось доказать.
Теорема 3. Пусть даны числа , каждое из которых меньше единицы. Тогда выполняется следующее неравенство:
Причем равенство возможно лишь при условии
Доказательство. Запишем неравенство Коши для чисел .
Используя свойства логарифма числа, преобразуем это выражение следующим образом:
или
что и требовалось доказать.
Замечание 3. Пусть даны положительные числа и . Тогда выполняются неравенства
причем равенство возможно лишь при условии 
.
Литература:
- Н. Я. Виленкин / Алгебра для 9 класса: Учеб. пособие для учащихся шк. и кл. с углубл. изуч. математикик / Н. Я. Виленкин, Г. С. Сурвилло, А. С. Симонов, А. И. Кудрявцев / — 3-е изд. — М.: Просвещение, 1999. — С.384: ил. — ISBN 5–09–009020–3
- Н. К. Гульманов / Определение нового вида прогрессии, основанной на операции возведения в степень, и изучение ее основных свойств / Н. К. Гульманов, Н. А. Марчук // «Высокое качество и лидерство в образовании»: сборник докладов Международной научно-практической конференции (13–15 ноября 2013 года)/ АОО «Назарбаев Интеллектуальные школы». Часть 1. — Астана, 2013. — С. 120–124
- П. П. Коровкин / Неравенства / Популярные лекции по математике, выпуск № 5/ — М.: Издательство «Наука», 1974. — С. 54
- И. С. Соминский / Метод математической индукции / Популярные лекции по математике, выпуск № 3/ — М.: Издательство «Наука», 1972. — С. 63
