В работе рассматривается распространение волн в двухслойном цилиндрическом теле с идеальной жидкостью. Задача решается в потенциалах перемещений. Дисперсионное уравнение решается методом Мюллера.
Ключевые слова: фазовая скорость, продольные и поперечные волны, цилиндрическая оболочка
Поглощения продольных и поперечных волн в среде является одной из важных характеристик, используемых в промысловой и разведочной геофизике. Чаще всего такие параметры определяет с помощью скважинных измерений методом акустического каротажа. Однако, если измерение затухания продольной волны Р не вызывает больших затруднений, так как она образует первые вступления, то определение поглощения поперечной волны S является более сложной задачей, поскольку она вступает на фоне сильных интерференционных колебаний, вызываемых резонансными явлениями в скважине [1, 2]. Все эти данные позволяют провести теоретические исследования затухания свободных волн в скважине с коэффициентами затухания Р — и S — волн. Пусть, окружающая скважину среда является твердой, скорость продольных волн в ней обозначим через Ср2, СS2, (-<z< r="" ,="">r0) и скорости распространение волн в жидкости Ср1(rr0, -<z< <="" p="" в="" волн,="" волновым="" потенциалы="" распространяющихся="" системе,="" скоростей="" такой="" удовлетворяют="" уравнениям:="" ).="">
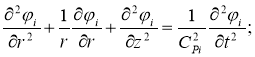 (i=1,2)
(i=1,2) 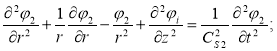
На границе r=r0 требуется выполнение с условиями непрерывности нормальных составляющих смещений и напряжений и равенства нулю касательных напряжений:
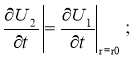
![]()
![]()
В такой системе могут распространяться осесимметричные нормальные волны двух типов, различающиеся характером дисперсии и диапазоном изменения фазовых скоростей как функции частоты. Один тип волн, условно называемый гидроволновой, имеет фазовые скорости, всегда меньше скорости звука в жидкости. Дисперсионное уравнение для него записывается в виде:
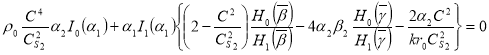 (1)
(1)
Где:
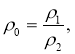
![]()
![]()
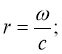
![]()
![]()
![]()
С фазовая скорость волн; ![]() плотности материала;
плотности материала; ![]() функции Бесселя и Ханкеля нулевого и первого порядки [1]. Дисперсионное уравнение (1) решается методом Мюллера.
функции Бесселя и Ханкеля нулевого и первого порядки [1]. Дисперсионное уравнение (1) решается методом Мюллера.
Рассмотрим собственный колебания двухслойный цилиндрической оболочке находящиеся в упругой среде, обозначим через Сpi, Сsi, i, i, i (I=1,2,3) соответственно скорость продольной и поперечной волны, плотность и модуль упругости. Рассмотрим задачу о распространении свободных волн, возникающих в такой системе. Уравнения движения среды для продольных i и поперечных i потенциалов представляется в виде: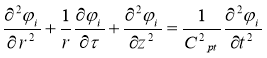 (2)
(2)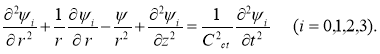
В уравнениях (2) следует подставить 2 =0, если в затрубном пространстве находится жидкость. Соответствующие напряжения rr,r![]() и смещения ur, uz определяются через потенциалы i, равенствами:
и смещения ur, uz определяются через потенциалы i, равенствами:
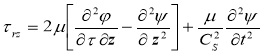 ,
, 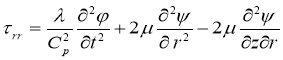
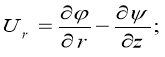
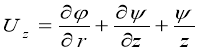 .
.
На границах раздела упругой среды с жидкостью выполняются граничные условия непрерывности нормальных составляющих смещений и напряжений, а также равенство нулю касательных напряжений в твердом теле:
![]()
![]()
![]() (3, a)
(3, a)
![]()
![]()
![]()
![]()
![]()
![]()
Если жидкость заменена упругой средой, то на контакте двух сред ставятся следующие условия:
![]()
![]()
![]()
![]()
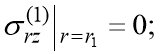
![]()
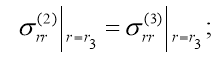
![]() (3, b)
(3, b)
Решения уравнений (2), удовлетворяют условию конечности в точке r=0 и условиям убывания на бесконечности и выражаются через модифицированные функции Бесселя.
На границе контакта слоев r=r2 ставится условие жесткого (или скользящего) контакта (непрерывны нормальные составляющие напряжений и смещений, отсутствуют касательные составляющие напряжений) и контакт между внешним слоем и окружающей средой жесткий (непрерывны нормальные и тангенциальные составляющие напряжений и смещений). Дисперсионное уравнение записывается в виде:
(k,)=0(4)
Оно представимо в виде определителя, у которого элементы ij (1i1), (1 j 1), отличные от нуля, имеют следующий вид:
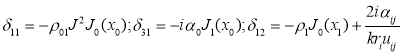 ,
,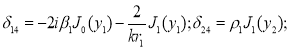
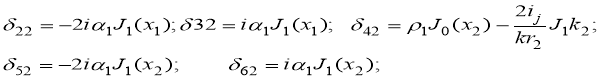
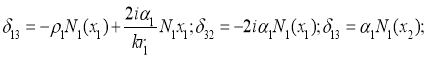
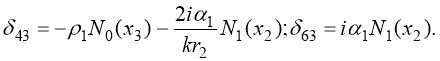
Остальные элементы также записываются в аналогичном виде.
Здесь x0=-ikr1α0; x1=-ikr1α1; x2=-ikr2α0; x3=-ikr2α2;y1=-ikr1β1, в двухслойном цилиндре V определяет скорость обобщенной волны по двухслойному цилиндру. Фазовая скорость волны определяется величиной реальной части корня, величины мнимой части корня связаны с затуханием χ на единице расстояния зависимостью:
![]()
Дисперсионное уравнения (4) решается методом Мюллера. Значение левой части на каждой итерации метода Мюллера определяется методом Гаусса с выделением главного элемента. Нами были составлены программы и проведены расчеты дисперсии и затухания волны Лэмба для моделей скважин, описываемых граничными условиями (3, a) и (3, b). Исходя из физической постановки задачи, будем считать, что поглощением обладают буровая жидкость, цемент, тампонажная смесь, поглощением же в материале колонны и в окружающей среде будем пренебрегать. Переход к системе с поглощением был сделан посредством введения комплексных параметров сред. Численные результаты получены при следующих значениях параметров:
Сpo= 1500 м/c; Сp1= 1500 м/c; Сp2= 1500 м/c;
Сp3= 5300 м/c; Сs1= 2900 м/c; Сs2= 2000 м/c;
Сs3= 2000 м/c; ρ0= 1 г/см3; ρ1= 8 г/см3;
ρ 2= 3 г/см3; ρ4= 4 г/см3; r1=0.05 м;
r2=0.06 м; r3=0.067 м.
Результаты расчетов представлены в таблице. Видно, что фазовая скорость слабо зависит от волнового числа.
Таблица 1
Изменение фазовой скорости С (м/с) взависимости от волнового числа (α/a))
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
1450,121 |
1450,024 |
1451,01 |
1456,28 |
1450,82 |
|
2 |
1456,3 |
1456,09 |
1456,013 |
1456,72 |
1455,3 |
|
3 |
1462,24 |
1462,50 |
1462,03 |
1462,4 |
1461,9 |
Из анализа значений фазовой скорости выявлено, что разница между скоростями осесимметричных и неосесимметричных волн первой моды мала для всех значений волнового числа, кроме близких к нулю (область очень длинных волн), а минимумы части первой моды для всех значений n совпадают, так что и в данном случае первая резонансная скорость может быть определена из решения соответствующей осесимметричной задачи.
Литература:
- Айнола Л. А., Нигул У. К. Волновые процессы деформации упругих плит и оболочек. — Изв. АН Эст. ССР, 1965, 14, № 1, с. 3–63.
- Викторов И. А. Ультразвуковые волны Лэмба. — Акуст. ж. 1965, II, вып. I, с. 1–18.

