Задача о распространении волн в цилиндрической оболочке, заполненной или погруженной жидкость, имеет важное прикладное значение. Явление распространения волнообразного движения жидкости в упругих цилиндрических оболочках привлекало внимание исследователей [1, 2, 3, 4]. В этих работах, посвященных волновым процессам в системе упругой цилиндрической оболочки, рассматривается идеальная жидкость, используются классические и уточненные уравнения оболочек, рассмотрено влияние радиальных и продольных инерционных сил, учтена средняя плотность потока жидкости или газа. В работах [5, 6] проводится анализ закономерностей волнового процесса в упругой оболочке с вязкой жидкостью в рамках модели линеаризированных уравнений гидродинамики вязкой сжимаемой жидкости. В данной статье рассматриваются отличия систем цилиндрических оболочек (упругих или вязкоупругих) с жидкостью (идеальной или вязкой) от других, данная система рассматривается как диссипативно неоднородная механическая система [7, 8, 9].
Ключевые слова: цилиндрическая оболочка, жидкость, волновой процесс, диссипативно неоднородная, волнообразные движения
Постановка задача иметоды решения.
Рассматривается бесконечная по длине деформируемая (упругая или вязкоупругая) цилиндрическая оболочка радиуса R с постоянными толщиной ![]() , плотностью
, плотностью ![]() , модулем Юнга Е,
, модулем Юнга Е, ![]() — коэффициенты демпфирования в осевом и радиальном направлениях; коэффициентом Пуассона
— коэффициенты демпфирования в осевом и радиальном направлениях; коэффициентом Пуассона ![]() , заполненная вязкой жидкостью с плотностью в равновесном состоянии. Подлежат исследованию совместные колебания оболочки и жидкости, гармонические по осевой координате z и экспоненциально затухающие по времени, либо гармонические по времени и затухающие по z. Амплитуды колебаний считаются малыми, что позволяет записать основные соотношения в рамках линейной теории. Полную систему линеаризованных уравнений движения вязкой баротропной можно представить в виде [3]
, заполненная вязкой жидкостью с плотностью в равновесном состоянии. Подлежат исследованию совместные колебания оболочки и жидкости, гармонические по осевой координате z и экспоненциально затухающие по времени, либо гармонические по времени и затухающие по z. Амплитуды колебаний считаются малыми, что позволяет записать основные соотношения в рамках линейной теории. Полную систему линеаризованных уравнений движения вязкой баротропной можно представить в виде [3]
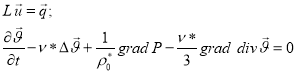
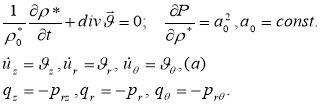
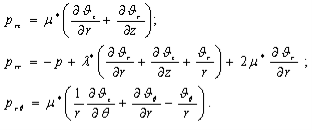 (1)
(1)
Здесь L – матрица дифференциальных операторов теории типа Крихгофа-Лява (или С. П. Тимошенко) [3]; ![]() – вектор перемещений точек срединой поверхности оболочки, причем для оболочек Кирхгофа-Лява он имеет размерность равную трем
– вектор перемещений точек срединой поверхности оболочки, причем для оболочек Кирхгофа-Лява он имеет размерность равную трем ![]() , а для оболочек типа Тимошенко размерность вектора
, а для оболочек типа Тимошенко размерность вектора ![]() равно пяти. Здесь кроме осевого, окружного и нормального перемещений добавляются еще углы поворота нормали к срединой поверхности в осевом и окружном направлениях;
равно пяти. Здесь кроме осевого, окружного и нормального перемещений добавляются еще углы поворота нормали к срединой поверхности в осевом и окружном направлениях; ![]() вектор усилия внешней нагрузки, приведенный к срединной поверхности оболочки. В уравнениях (1)
вектор усилия внешней нагрузки, приведенный к срединной поверхности оболочки. В уравнениях (1) ![]() =
= ![]() – вектор скорости частиц жидкости;
– вектор скорости частиц жидкости; ![]() и Р – возмущения плотности и давления в жидкости;
и Р – возмущения плотности и давления в жидкости; ![]() и а0 – плотность и скорость звука в жидкости в состоянии покоя;
и а0 – плотность и скорость звука в жидкости в состоянии покоя; ![]() — кинематический и динамический коэффициенты вязкости; для второго коэффициента вязкости
— кинематический и динамический коэффициенты вязкости; для второго коэффициента вязкости ![]() принято соотношение
принято соотношение ![]() =
=![]() ;
; ![]() – cоставляющие тензора напряжений в жидкости. Уравнений (1а) соответственно кинематические и динамические граничные условия, которые, в силу тонкостенности оболочки, будем удовлетворять на срединной поверхности (r=R). Соотношения (1) представляет замкнутую систему соотношений гидровязкоупругости для цилиндрической оболочки, содержащей вязкую сжимаемую жидкость. Так для оболочек, подчиняющихся гипотезе Кирхгофа-Лява, L – матрица дифференциальных операторов может записать:
– cоставляющие тензора напряжений в жидкости. Уравнений (1а) соответственно кинематические и динамические граничные условия, которые, в силу тонкостенности оболочки, будем удовлетворять на срединной поверхности (r=R). Соотношения (1) представляет замкнутую систему соотношений гидровязкоупругости для цилиндрической оболочки, содержащей вязкую сжимаемую жидкость. Так для оболочек, подчиняющихся гипотезе Кирхгофа-Лява, L – матрица дифференциальных операторов может записать:
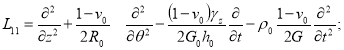
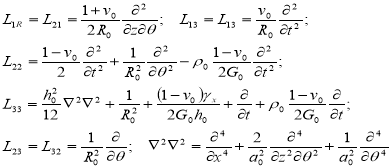 (2)
(2)
Компоненты вектора нагрузок для оболочек Кирхгофа-Лява имеют вид
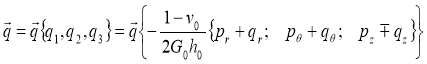 (3)
(3)
где знак мине отвечает внутренней оболочке, а знак плюс-наружной ![]() — компоненты реакции со стороны жидкости (заполнителя);
— компоненты реакции со стороны жидкости (заполнителя); ![]() – интенсивность заданной нагрузки в соответствующем направлении. В осесимметричном случае на оси г=0 должны выполняться условия
– интенсивность заданной нагрузки в соответствующем направлении. В осесимметричном случае на оси г=0 должны выполняться условия ![]() ,
, ![]() =0. Если внешняя поверхность г=R предполагается неподвижной, тогда ur=uz=uφ=0. Раскрывая уравнения (1) в координатной форме, нетрудно заметить, что соотношения (1)-(3) распадаются на независимые краевые задачи:
=0. Если внешняя поверхность г=R предполагается неподвижной, тогда ur=uz=uφ=0. Раскрывая уравнения (1) в координатной форме, нетрудно заметить, что соотношения (1)-(3) распадаются на независимые краевые задачи:
– крутильные колебания:
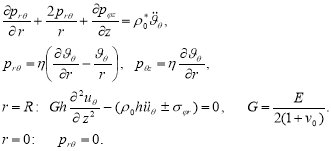 (4)
(4)
– продольно-поперечные колебания:
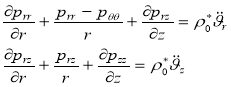
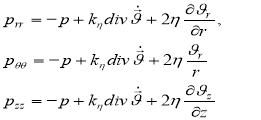 (5)
(5)
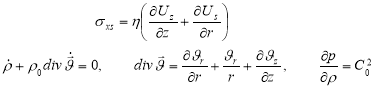
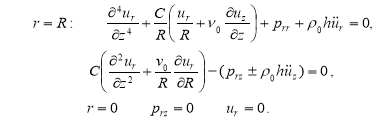
Пусть волновой процесс периодичен по z и затухает по времени, тогда задаётся действительное волновое число k, а комплексная частота является искомым собственным значением. Решения краевых задач (1)-(3) для основных неизвестных, удовлетворяющие наложенным выше ограничениям на зависимость по времени и координате z, следует искать в виде [3]
![]() (6)
(6)
где вектор в правой части есть искомая комплекснозначная функция аргумента r, k, ![]() суть известного действительного и спектрального комплексного параметра от типа задачи. Суперпозиция решений (6) образует экспоненциально затухающую по времени стоячую волну, которая описывает собственные колебания жидкости и цилиндрической оболочки конечной длины с краевыми условиями. При бесконечной длине оболочки по аналогии указанный тип движения (6) будем называть собственными или свободными колебаниями. В случае стационарного по времени и затухающего по координате процесса, наоборот, известной является действительная частота
суть известного действительного и спектрального комплексного параметра от типа задачи. Суперпозиция решений (6) образует экспоненциально затухающую по времени стоячую волну, которая описывает собственные колебания жидкости и цилиндрической оболочки конечной длины с краевыми условиями. При бесконечной длине оболочки по аналогии указанный тип движения (6) будем называть собственными или свободными колебаниями. В случае стационарного по времени и затухающего по координате процесса, наоборот, известной является действительная частота ![]() , а искомым –комплексное волновое число k. В отличии от собственных, эти колебания условимся называть установившимися. Действительные части величин
, а искомым –комплексное волновое число k. В отличии от собственных, эти колебания условимся называть установившимися. Действительные части величин ![]() в первом случае, и k, во втором имеют физический смысл частот процесса по времени и координате соответственно. Мнимые части — скорость затухания волновых процессов по времени и Z соответственно [4]. Величину 1/Imk иногда определяют как интервал распространения затухающей волны. В предельном упругом случае интервал распространения бесконечен. Степень затухания волнового процесса на временном периоде характеризуется логарифмическим декрементом
в первом случае, и k, во втором имеют физический смысл частот процесса по времени и координате соответственно. Мнимые части — скорость затухания волновых процессов по времени и Z соответственно [4]. Величину 1/Imk иногда определяют как интервал распространения затухающей волны. В предельном упругом случае интервал распространения бесконечен. Степень затухания волнового процесса на временном периоде характеризуется логарифмическим декрементом ![]() ,аналогично пространственный декремент равен
,аналогично пространственный декремент равен
![]() .
.
Можно ввести также понятия фазовых скоростей распространения собственных и установившихся движений
![]()
![]() (7)
(7)
Продольно— поперечные колебания.
В этом параграфе проводится анализ стационарных продольно-поперечных колебаний оболочки, заполненной жидкостью, которые в соответствии с (5) могут быть описаны системой четырех обыкновенных дифференциальных уравнений
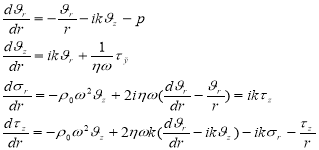 (8)
(8)
С краевыми условиями
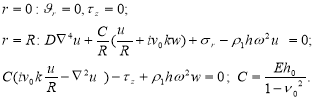 (9)
(9)
Величина р в первом уравнении системы (8) определяется через основные неизвестные согласно выражению
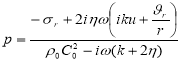 (10)
(10)
Спектральная задача (8), (9), как и в случае продольно — поперечные колебания, решались методом ортогональной прогонки. Для нахождения корней характеристического уравнения использовался метод Мюллера.
Численные результаты.
Приведем результаты численного исследования собственных колебаний. На рис.1 показаны дисперсионные кривые зависимости ![]() от волнового числа k — для случаев несжимаемой (С0 =
от волнового числа k — для случаев несжимаемой (С0 = ![]() – штрихпунктирные линии) и сжимаемой (С0=0,1 — сплошные линии) жидкости. Параметры оболочки и коэффициенты вязкости приняты следующими:
– штрихпунктирные линии) и сжимаемой (С0=0,1 — сплошные линии) жидкости. Параметры оболочки и коэффициенты вязкости приняты следующими:
h0 = 0,05; р=1,8; v0 = 0,25; h=6,011*10(-4); к=-2 η/3. Здесь и далее приводятся безразмерные величины, для которых единицы длины, времени и массовой плотности суть 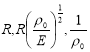 . Для несжимаемой жидкости существуют две моды, соответствующие преимущественно продольным (кривая 1) и преимущественно поперечным (кривая 2) колебаниям оболочки, с комплексными собственными значениями. Все остальные собственные движения имеют мнимые собственные значения, то есть апериодичны по времени. Пунктирными линиями на рис.1 обозначены дисперсионные кривые, соответствующие колебаниям оболочки с идеальной несжимаемой жидкостью. Решение последней задачи приводится ниже. Следует отметить, что в отличие от колебаний сухой оболочки совместные поперечные колебания оболочки жидкости для указанной плотности p1, происходит на меньшей по сравнению с продольными колебаниями частоте во всем диапазоне изменения волнового числа. При введении вязкости частота колебаний первой моды снижается, по-видимому, за счет вовлечения в движение дополнительных масс жидкости в пограничном слое, а у второй моды появляется критическое волновое число, ограничивающее область колебательных движений снизу. В работе [2], исследовавших установившиеся колебания, отмечалось стремление к нулю фазовой скорости низшей моды при уменьшении частоты. Собственные движения оболочки и вязкой сжимаемой жидкости имеют бесконечное число мод. В работе [3], использующего асимптотические методы решения, последний эффект обнаружить не удалось. На рис. 2 приводятся дисперсионные кривые для первых четырех мод с минимальными частотами колебаний (кривые 3,4,5,6) в порядке возрастания величины
. Для несжимаемой жидкости существуют две моды, соответствующие преимущественно продольным (кривая 1) и преимущественно поперечным (кривая 2) колебаниям оболочки, с комплексными собственными значениями. Все остальные собственные движения имеют мнимые собственные значения, то есть апериодичны по времени. Пунктирными линиями на рис.1 обозначены дисперсионные кривые, соответствующие колебаниям оболочки с идеальной несжимаемой жидкостью. Решение последней задачи приводится ниже. Следует отметить, что в отличие от колебаний сухой оболочки совместные поперечные колебания оболочки жидкости для указанной плотности p1, происходит на меньшей по сравнению с продольными колебаниями частоте во всем диапазоне изменения волнового числа. При введении вязкости частота колебаний первой моды снижается, по-видимому, за счет вовлечения в движение дополнительных масс жидкости в пограничном слое, а у второй моды появляется критическое волновое число, ограничивающее область колебательных движений снизу. В работе [2], исследовавших установившиеся колебания, отмечалось стремление к нулю фазовой скорости низшей моды при уменьшении частоты. Собственные движения оболочки и вязкой сжимаемой жидкости имеют бесконечное число мод. В работе [3], использующего асимптотические методы решения, последний эффект обнаружить не удалось. На рис. 2 приводятся дисперсионные кривые для первых четырех мод с минимальными частотами колебаний (кривые 3,4,5,6) в порядке возрастания величины ![]() . Сравнивая кривые 1,2 и 3,4 между собой, можно убедиться, что вторая несколько хуже первой моды колебаний системы оболочка — сжимаемая жидкость для выбранных параметров удовлетворительно описываются моделью несжимаемой жидкости в области волновых чисел k < 1. Это дает основание при исследовании указанной системы в первом приближении пренебречь сжимаемостью жидкости.
. Сравнивая кривые 1,2 и 3,4 между собой, можно убедиться, что вторая несколько хуже первой моды колебаний системы оболочка — сжимаемая жидкость для выбранных параметров удовлетворительно описываются моделью несжимаемой жидкости в области волновых чисел k < 1. Это дает основание при исследовании указанной системы в первом приближении пренебречь сжимаемостью жидкости.
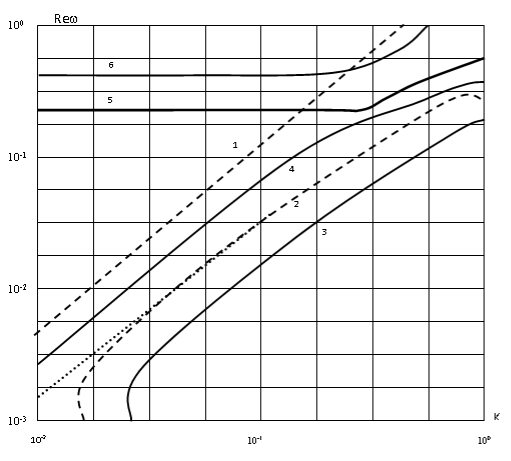
Рис. 1. Зависимость Re со от волнового число K (для случая несжимаемой жидкости)
Система упругая оболочка — вязкая жидкость является диссипативно-неоднородным вязкоупругим телом при радиальной координате. При этом в отличии от рассмотренных ранее крутильных колебаний здесь для несжимаемой жидкости имеются две, а для сжимаемой — неограниченное число колебательных мод. Представляет интерес выяснить, насколько в этой системе может проявиться синергический эффект. На рис.2 показаны дисперсионные кривые (1,2) для следующих параметров оболочки и жидкости:
![]()
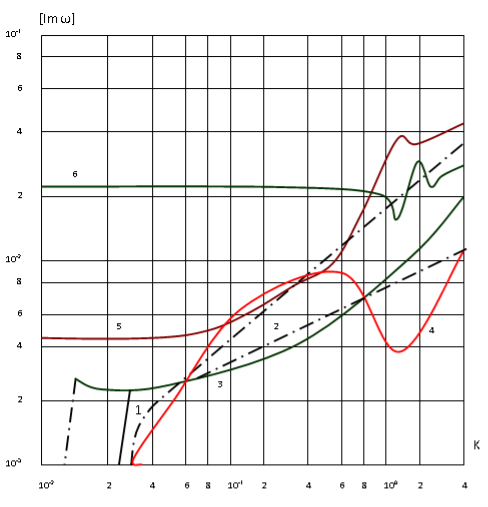
Рис. 2. Зависимость Im от волнового число K (для случая сжимаемой жидкости)
Штрихпунктирные линии соответствуют колебаниям сухой оболочки. Пунктирными линиями отмечены частотные зависимости для случая идеальной жидкости v = 0. В противоположность ранее рассмотренному варианту с плотностью р = 8, в данном случае парциальные частоты (v = 0) продольных и поперечных колебаний оболочки с идеальной жидкостью пересекаются между собой. Естественно ожидать, что при v вблизи точки пересечения парциальных частот будет иметь место сильная связанность обеих мод, приводящая к повышенной энергии, что выражается в синергическом эффекте. Действительно, о наличии мод свидетельствует эффект Вина – превращение продольной моды в поперечную, а поперечной в продольную при изменении волнового числа в окрестности пересечения парциальных частот. Нарушение монотонности роста и синергического эффекта. По сравнению с предыдущими описаниями этого эффекта здесь имеются две особенности. Во-первых, эффект проявляется вдали от места приближения кривых ![]() двух мод, во-вторых, кривые коэффициентов демпфирования не пересекаются между собой. В работе [6] исследовал связанность совместных колебаний идеального сжимаемого газа и оболочки с помощью диаграмм Вина. В качестве парциальных он рассмотрел частоты колебаний газа в жестких стенках и пустой оболочке. Возвращаясь к рис.2 отметим аналогичное проявление эффекта Вина в местах сближения кривых 4,5 и 5,6. В этих же местах на рис. 3 наблюдается для синергического эффекта кривых. Интересно проследить также влияние вязкости жидкости на связанность мод. Кривые 3,4 на рис.4 соответствуют значению коэффициента вязкости η=0,11 при неизменных остальных параметрах. В этом случае мода преимущественно поперечных колебаний определена на конечном интервале изменение волнового числа, а эффект Вина не наблюдается, что свидетельствует о слабой связанности мод. Еще большой рост вязкости (η=0,13, кривая 5) приводит к тому, что мода поперечных колебаний становится всюду апериодичной, а у продольных колебаний появляется критическое волновое число, ограничивающее область колебательных движений сверху. Физическая сущность обнаруженного эффекта раскрывается при анализе колебаний оболочки, заполненной идеальной жидкостью. Уравнения гармонических колебаний идеальной жидкости нетрудно вывести из соотношений (8), формально положив коэффициенты вязкости равными нулю.
двух мод, во-вторых, кривые коэффициентов демпфирования не пересекаются между собой. В работе [6] исследовал связанность совместных колебаний идеального сжимаемого газа и оболочки с помощью диаграмм Вина. В качестве парциальных он рассмотрел частоты колебаний газа в жестких стенках и пустой оболочке. Возвращаясь к рис.2 отметим аналогичное проявление эффекта Вина в местах сближения кривых 4,5 и 5,6. В этих же местах на рис. 3 наблюдается для синергического эффекта кривых. Интересно проследить также влияние вязкости жидкости на связанность мод. Кривые 3,4 на рис.4 соответствуют значению коэффициента вязкости η=0,11 при неизменных остальных параметрах. В этом случае мода преимущественно поперечных колебаний определена на конечном интервале изменение волнового числа, а эффект Вина не наблюдается, что свидетельствует о слабой связанности мод. Еще большой рост вязкости (η=0,13, кривая 5) приводит к тому, что мода поперечных колебаний становится всюду апериодичной, а у продольных колебаний появляется критическое волновое число, ограничивающее область колебательных движений сверху. Физическая сущность обнаруженного эффекта раскрывается при анализе колебаний оболочки, заполненной идеальной жидкостью. Уравнения гармонических колебаний идеальной жидкости нетрудно вывести из соотношений (8), формально положив коэффициенты вязкости равными нулю.
![]() (11)
(11)
общее решение системы (12), удовлетворяющее условию конечности неизвестных в нуле, имеет вид
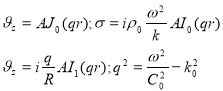 (12)
(12)
где А произвольная постоянная:J0, Jl,- функции Бесселя нулевого и первого порядка соответственно для несжимаемой жидкости существует две действительные собственные функции Бесселя I0 и I1
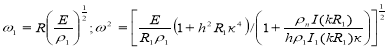 (13)
(13)
В отличие от сухой оболочки здесь у второй частота запирания отсутствует, а фазовая скорость при малых k равна величине ![]() , которая совпадает со скоростью волны Резаля (см. обзор в начале главы). В случае сжимаемой жидкости
, которая совпадает со скоростью волны Резаля (см. обзор в начале главы). В случае сжимаемой жидкости ![]() и предельная фазовая скорость моды поперечных колебаний оболочки при k —> 0 есть скорость волны Кортевега- Жуковского
и предельная фазовая скорость моды поперечных колебаний оболочки при k —> 0 есть скорость волны Кортевега- Жуковского ![]() . Численное исследование показало, что критическое значение Ck не зависит от вязкости жидкости, но с ростом величины η ослабевает зависимость колебаний коэффициента Пуассона, так что отношение
. Численное исследование показало, что критическое значение Ck не зависит от вязкости жидкости, но с ростом величины η ослабевает зависимость колебаний коэффициента Пуассона, так что отношение ![]() а собственная форма U становится плоской. Как следует из приведенных результатов, в целом в рамках инженерной постановки задачи, нельзя адекватно описать продольные колебания цилиндрической оболочки, заполненной вязкой жидкостью с помощью стержневой теории.
а собственная форма U становится плоской. Как следует из приведенных результатов, в целом в рамках инженерной постановки задачи, нельзя адекватно описать продольные колебания цилиндрической оболочки, заполненной вязкой жидкостью с помощью стержневой теории.
Литература:
- Тер-Акопянц Г. Л. Об уточнении результатов влияния жидкости на распространение волн в упругой цилиндрической оболочке // Журнал. Фундаментальные исследования, технические науки № 10, 2013 г. С. 516–520.
- Сафаров И. И. Колебания и волны в диссипативно недородных средах и конструкциях. – Тошкент. Фан, 1992. – 250 с.
- Сафаров И. И., Тешаев М. Х., Болтаев З. И. Волновые процессы в механическом волноводе. LAP LAMBERT Academic publishing (Германия). 2012., 217 с.
- Бозоров М. Б., Сафаров И. И., Шокин Ю. И. Численное моделирование колебаний диссипативно однородных и неоднородных механических систем. СО РАН, Новосибирск, 1996, 188 с.
- Каюмов С. С., Сафаров И. И. Распространение и дифракция волн в диссипативно — неоднородных цилиндрических деформируемых механических систем. Ташкент: ФАН, 2002 г, 214 с.
- Фролов К. В., Антонов А. Н. Колебания оболочек жидкости – М.: Наука, 1983. 365 с.
- Sorokin S. V. Fluid-Structure Interaction and Structural Acoustics. Book of Lecture Notes. — Technical University of Denmark, 1997. — 188 p.
- Вольмир А. С. Оболочки в потоке жидкости и газа: Задачи гидроупругости. — М.: Наука.1979. — 320 с.
- Гузь А. Н. Распространение волн в цилиндрической оболочке с вязкой сжимаемой жидкостью // Прикл. Механика. – 1980. – 16, № 10. – С. 10–20.

