В статье рассматриваются методы математического моделирования автоколебаний тока в электрических цепях с нелинейными элементами. Приводятся основные дифференциальные уравнения, описывающие динамику тока в контуре с индуктивностью, емкостью и нелинейным элементом. Особое внимание уделяется примеру генератора Ван дер Поля, описывающего автоколебания в нелинейных системах. Также рассматриваются численные методы, такие как метод Рунге-Кутты, для решения нелинейных дифференциальных уравнений и моделирования автоколебательных процессов.
Ключевые слова: автоколебания тока, математическое моделирование, электрическая цепь, нелинейные системы, генератор Ван дер Поля, дифференциальные уравнения, численные методы, метод Рунге-Кутты.
Введение
Автоколебания являются важным явлением в физике и инженерии, поскольку они встречаются в различных системах, от механических осцилляторов до электрических цепей. В контексте электрических цепей автоколебания тока представляют собой периодические колебания в системах без внешнего периодического воздействия. Эти колебания могут возникать за счет нелинейных свойств элементов цепи, таких как катушки индуктивности, конденсаторы и активные элементы.
Математическое моделирование автоколебаний тока является мощным инструментом для изучения динамических свойств таких систем. В данной статье рассмотрим основы математического моделирования автоколебаний тока в электрических цепях и исследуем основные уравнения, описывающие такие процессы.
Автоколебания возникают в нелинейных системах, которые обладают внутренней обратной связью, способной поддерживать колебательный процесс. В контексте электрических цепей автоколебания часто можно наблюдать в колебательных контурах, содержащих индуктивность L, емкость C и нелинейные элементы, такие как транзисторы или тиристоры.
Простым примером автоколебательной системы является колебательный контур с отрицательным сопротивлением. Этот контур может быть представлен схемой с индуктивностью L, емкостью C и нелинейным элементом, который создает условия для автоколебаний.
Дифференциальные уравнения для автоколебаний тока
Математическое описание автоколебаний тока основывается на уравнениях, связывающих напряжение и ток через компоненты цепи. Для электрического контура, состоящего из индуктивности L, емкости C и сопротивления R, а также нелинейного элемента с характеристикой I=f(V), основным уравнением динамики будет второе дифференциальное уравнение:
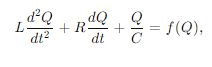
где:
— Q — заряд на конденсаторе;
— L — индуктивность;
— R — сопротивление;
— C — емкость;
— f(Q) — нелинейная функция, описывающая зависимость тока от напряжения или заряда в нелинейном элементе.
Для простоты можно рассматривать нелинейный элемент, имеющий кусочно-линейную зависимость f(Q), что позволяет аналитически изучать поведение системы.
Пример автоколебательной системы: генератор Ван дер Поля
Одним из классических примеров нелинейных систем, демонстрирующих автоколебания, является генератор Ван дер Поля. Это система, описываемая дифференциальным уравнением второго порядка:
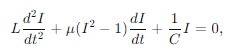
где I — ток в контуре, L — индуктивность, C — емкость, а μ — параметр, описывающий степень нелинейности системы.
Уравнение Ван дер Поля описывает систему с затухающими и нарастающими колебаниями, что приводит к установившимся автоколебаниям при определенных условиях. Это уравнение находит применение в различных областях, включая изучение радиотехнических цепей и биофизических процессов.
Численные методы для моделирования автоколебаний
Из-за сложности аналитического решения нелинейных уравнений, описывающих автоколебания, часто прибегают к численным методам. Один из распространенных подходов — метод Рунге-Кутты, который позволяет решать дифференциальные уравнения второго порядка с высокой точностью. Численное моделирование может быть реализовано с помощью программ, таких как MATLAB, Python (SciPy), или специализированных программ для моделирования электрических цепей, таких как LTspice.
Пример численного решения уравнения Ван дер Пау методом Рунге-Кутты в python может выглядеть следующим образом:
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
def van_der_pohl(t, y, mu):
return [y [1], mu * (1 — y [0]**2) * y [1] — y [0]]
mu = 1.0
y0 = [2.0, 0.0] # Начальные условия
t_span = (0, 50)
t_eval = np.linspace(*t_span, 1000)
sol = solve_ivp(van_der_pohl, t_span, y0, args=(mu,), t_eval=t_eval)
plt.plot(sol.t, sol.y [0])
plt.xlabel('Время')
plt.ylabel('Ток')
plt.title('Автоколебания тока в генераторе Ван дер Поля')
plt.show()
Математическое моделирование автоколебаний тока играет важную роль в понимании и исследовании динамических свойств электрических цепей. Оно позволяет не только предсказывать поведение систем, но и проектировать устройства, такие как генераторы и осцилляторы, на основе их нелинейных характеристик. Численные методы, такие как метод Рунге-Кутты, открывают возможности для исследования сложных систем, которые не могут быть решены аналитически. В будущем исследование автоколебаний тока будет оставаться актуальной темой в контексте разработки новых электронных устройств, а также в междисциплинарных областях, таких как биофизика и теоретическая электроника.
Литература:
- N., Abdullaeva N. U., Mirkomilova M. S., Shukurova D. M. The mechanism of current auto-oscillations in compensated silicon doped with impurity atoms
- Фотоэлементы на основе кремния с бинарными соединениями GexSi1-x Н. Ф. Зикриллаев, К. С. Аюпов, Ф. Э. Уракова, Н. У. Абдуллаева
- Zikrillayev N. F., Ayupov K. S., Abdullayeva N. U. The Mechanism of current auto-oscillations in compensated silicon doped with impurity atoms — 2024.

