В работе рассмотрен случай прохождения дифрагированной волны за упругим препятствием. Показано, что в материале препятствия продольная дифрагированная волна вызывает только продольную волну, интенсивность которой отличается от интенсивности дифрагированной волны коэффициентом, зависящим от отношения плотностей и отношения упругих параметров материала упругой среды и материала препятствия. Предельная пластическая волна, распространяющаяся в материале препятствия, становится упругой. Ее относительная интенсивность определяется интенсивностью скорости за фронтом волны.
Ключевые слова: дифрагированная волна, продольная волна, упругая среда, пластическая волна.
The work is devoted to research of the case of passing diffractional wave behind elastic obstacle. It is shown that a longitudinal diffractional wave causes only a longitudinal wave in the material of the obstacle, the intensity of which differs from the intensity of the wave by coefficient, depending on the ratio of the density and the ratio of the elastic parameters of the elastic medium material of obstacle. Ultimate plastic wave, propagating in the obstacle material, becomes elastic. It’s relative intensity is determined by the intensity of the velocity behind the wave front.
Key words. Diffractional wave, longitudinal wave, elastic medium, plastic wave.
Рассмотрим случай прохождения дифрагированной волны 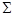 за упругим препятствием, ограниченным поверхностью
за упругим препятствием, ограниченным поверхностью 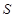 , внутри которого дифрагированная волна порождает возмущение в виде двух волн: продольной
, внутри которого дифрагированная волна порождает возмущение в виде двух волн: продольной 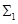 и сдвиговой
и сдвиговой 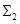 . Локальное представление о состоянии волн в момент их совместного распространения изображено на рис.1.
. Локальное представление о состоянии волн в момент их совместного распространения изображено на рис.1.
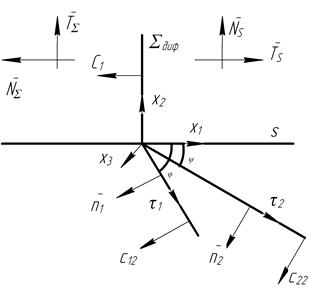
Рис.1. Схематическое изображение момента совместного распространения вдоль элемента поверхности 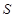 дифрагированной и двух порожденных в препятствии волн
дифрагированной и двух порожденных в препятствии волн
В соответствии с законом Снелла синусы углов, ориентирующих поверхности 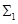 и
и 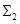 , определяются выражениями [2]:
, определяются выражениями [2]:
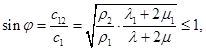
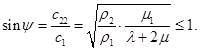 (1)
(1)
Здесь 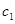 - скорость дифрагированной волны,
- скорость дифрагированной волны, 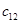 - скорость порожденной продольной волны,
- скорость порожденной продольной волны, 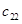 - скорость порожденной сдвиговой волны. Индекс «1» относится к параметрам материала препятствия.
- скорость порожденной сдвиговой волны. Индекс «1» относится к параметрам материала препятствия.
Из выражений для углов 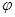 и
и 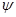 следует, что предложенная геометрическая картина не всегда имеет место, и в случае большей плотности
следует, что предложенная геометрическая картина не всегда имеет место, и в случае большей плотности 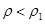 или большей упругости материала препятствия
или большей упругости материала препятствия 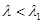 ,
, 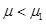 порожденные волны
порожденные волны 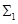 и
и 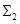 убегают вперед дифрагированной волны, а дифрагированная волна может порождать рэлеевские волны в препятствии.
убегают вперед дифрагированной волны, а дифрагированная волна может порождать рэлеевские волны в препятствии.
Для расчета напряженного состояния за фронтами сдвиговой 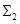 и продольной
и продольной 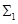 волн воспользуемся условием непрерывности напряжений на поверхности
волн воспользуемся условием непрерывности напряжений на поверхности 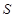 в области напряженного состояния материала, и условиями динамической совместности на продольной
в области напряженного состояния материала, и условиями динамической совместности на продольной 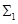 и сдвиговой
и сдвиговой 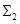 волнах.
волнах.
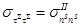 ,
, 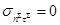 . (2)
. (2)
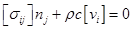 — на
— на 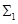 и на
и на 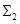 . (3)
. (3)
Преобразуем эти условия, введя интенсивности 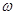 и
и 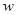 продольной и сдвиговой порожденных
продольной и сдвиговой порожденных 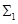 и
и 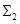 волн [4] так, что
волн [4] так, что
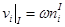 , то есть
, то есть 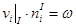 , где
, где 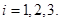 (4)
(4)
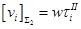 или
или 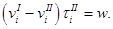 (5)
(5)
Для удобства в дальнейших расчетах выберем локальную систему координат 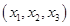 таким образом, чтобы направление
таким образом, чтобы направление 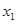 совпадало с направлением нормали дифрагированной поверхности
совпадало с направлением нормали дифрагированной поверхности 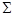 , а направление
, а направление 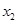 с направлением нормали к элементу поверхности
с направлением нормали к элементу поверхности 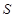 . Тогда система балансовых уравнений для интенсивностей порожденных волн примет вид:
. Тогда система балансовых уравнений для интенсивностей порожденных волн примет вид:
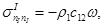 (6.1)
(6.1)
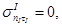 (6.2)
(6.2)
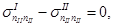 (6.3)
(6.3)
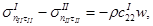 (6.4)
(6.4)
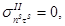 (6.5)
(6.5)
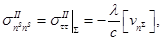 (6.6)
(6.6)
где
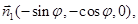
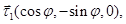
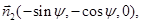
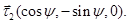
Балансовые уравнения на поверхности 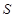 и на фронтах
и на фронтах 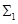 ,
, 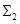 порожденных волн представляют собой:
порожденных волн представляют собой:
(6.1) — уравнение совместности напряжений и скорости волны на поверхности 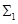 в проекции на нормаль к
в проекции на нормаль к 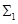 ;
;
(6.2) — условие совместности на поверхности 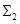 в проекции на касательную к
в проекции на касательную к 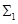 , то есть условие продольности волны
, то есть условие продольности волны 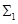 и условие отсутствия касательных напряжений за ней;
и условие отсутствия касательных напряжений за ней;
(6.3) — условие непрерывности нормальных напряжений на границе раздела двух материалов, а именно, внешней среды и материала;
(6.4) — условие совместности напряжений и скорости волны на фронте сдвиговой волны 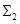 ;
;
(6.5) — условие отсутствия касательных напряжений на границе раздела двух материалов;
(6.6) — условие динамической совместности на фронте дифрагированной волны 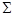 .
.
Для простоты обозначений нормальные и касательные напряжения будем писать с одним индексом:
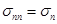 ,
, 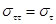 .
.
Заметим, что 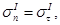
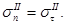
Тогда система уравнений для определения интенсивности порожденных волн примет вид:
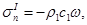 (7)
(7)
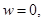 (8)
(8)
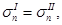 (9)
(9)
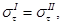 (10)
(10)
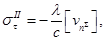 (11)
(11)
Учитывая соотношения (9), (10), (11), получим:
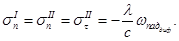 (12)
(12)
Полученные уравнения позволяют сделать вывод об отсутствии сдвиговой волны в материале препятствия, при этом интенсивность продольной волны в материале определяется:
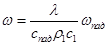 или
или 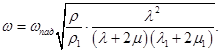 (13)
(13)
Проведенное исследование позволяет сделать вывод, что продольная дифрагированная волна вызывает в материале препятствия только продольную волну, интенсивность которой 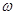 отличается от интенсивности дифрагированной волны коэффициентом, зависящим от отношения плотностей и отношения упругих параметров материала упругой среды и материала препятствия.
отличается от интенсивности дифрагированной волны коэффициентом, зависящим от отношения плотностей и отношения упругих параметров материала упругой среды и материала препятствия.
Область пространства, возмущенная дифрагированной волной в препятствии, определяется углом 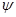 , величина которого определяется отношением упругих параметров окружающей среды и материала препятствия в соответствии с законом Снелла.
, величина которого определяется отношением упругих параметров окружающей среды и материала препятствия в соответствии с законом Снелла.
Для оценки напряженного состояния в материале препятствия проведем вычисление второго инварианта девиатора тензора напряжений для сравнения его с пределом пластичности в соответствии с условием Мизеса [3]:
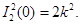 (14)
(14)
Скорость продольного деформирования упругого материала за фронтом дифрагированной волны порождает напряженное состояние, определяемое скачком напряжений:
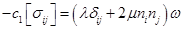 ,
, 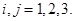 (15)
(15)
Заметим, что в случае покоя материала перед фронтом дифрагированной волны 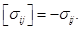
С учетом последнего из (15) получим:
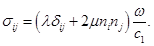
Второй инвариант девиатора тензора напряжений определяется выражением:
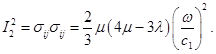 (16)
(16)
Предельная пластическая волна, распространяющаяся в материале препятствия, вызывает напряженное состояние, удовлетворяющее условию пластичности Мизеса (14), становится упругой, и ее относительная интенсивность определяется интенсивностью скорости за фронтом волны. В случае сферического препятствия интенсивность дифрагированной волны согласно, [1] определяется выражением:
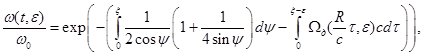
где 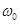 -значение интенсивности падающей волны на поверхности
-значение интенсивности падающей волны на поверхности 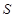 ,
, 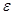 — поверхностная координата точки на дифрагированной волне,
— поверхностная координата точки на дифрагированной волне, 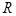 — радиус сферы (препятствия),
— радиус сферы (препятствия), 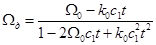 ,
,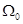 - средняя,
- средняя, 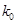 - гауссова кривизны дифрагированной поверхности.
- гауссова кривизны дифрагированной поверхности.
Литература:
1. Быкова К. И. Предельное напряженное состояние за дифрагированной пластической короткой волной на сфере / К. И. Быкова // Сборник статей по материалам международной научно-практической конференции. Ч.1.Чебоксары, 12–15 авг. 2013 г., с. 43–48.
2. Дэвид Бейли. Волоконная оптика: теория и практика// Дэвид Бейли, Эдвин Райт // Пер. с англ. — М.: КУДИЦ — ОБРАЗ, 2006.- 320 с.
3. Ивлев Д. Д. Механика пластических сред / Д. Д. Ивлев // М.: ФизМатЛит, 2001.-Т.1.- 448с.
4. Томас Т. Пластическое течение и разрушение в твердых телах / Т. Томас // М.: Мир, 1964.- 308с.

