В работе, на основе рассмотренной в [1] задачи динамической устойчивости сверхпроводящей замкнутой упругой сферической оболочки в однородном магнитном поле, получены области динамической устойчивости рассматриваемой оболочки и настроены графики зависимостей.
Ключевые слова: нестационарное магнитное поле, устойчивость
Введение: На основе выведенных основных уравнений и поверхностных условий, описывающие поведение сверхпроводящих замкнутых сферических оболочек в неоднородном магнитном поле, изучены возможности потери устойчивости оболочки под влиянием переменного магнитного поля и определены критические значения задачи.
Мат. модель задачи и методы решения: Рассмотрена задача динамической устойчивости сверхпроводящей замкнутой упругой сферической оболочки в однородном магнитном поле [1]
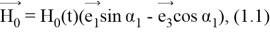
где
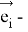
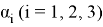
Добавочное магнитное поле
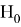
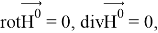
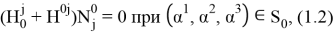
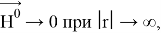
где
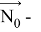
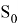
Таким образом,
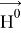
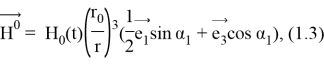
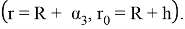
Невозмущенное магнитное поле
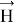
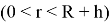
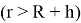
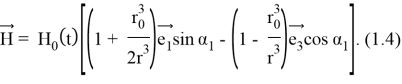
Подставляя (1.4) в систему
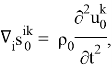
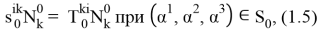
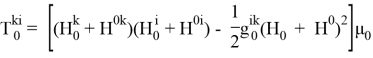
определяем поверхностную силу магнитного происхождения, действующую на оболочку в невозмущенном состоянии, используя (1.5), для отличных от нуля усилий невозмущенного состояния получаем следующие выражения:
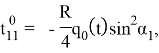
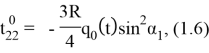
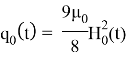
Определение индуцированного во внешней области магнитного поля
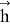
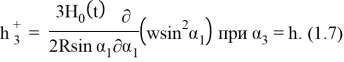
Решение указанной задачи Неймана определяется формулой Бьеркеса и имеет вид [1]
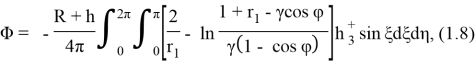
где
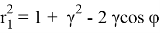
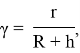
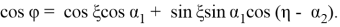
Используя (1.8) определяем
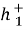
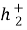
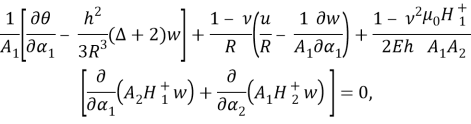
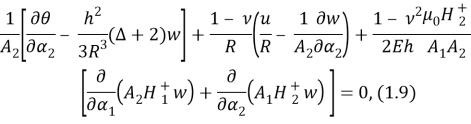
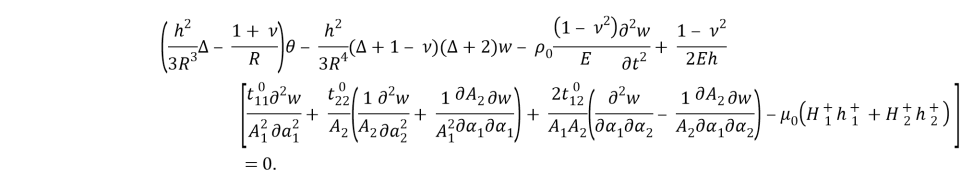
Здесь
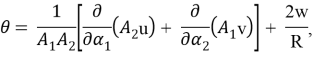
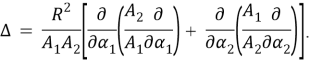
Остается подставить (1.4), (1.6) и найденные изложенным способом значения
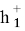
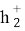
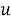
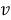
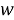
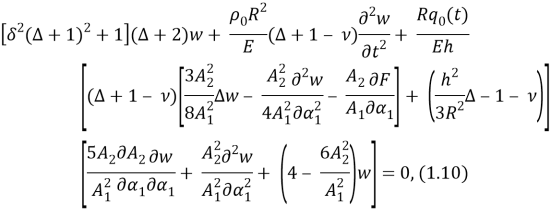
где
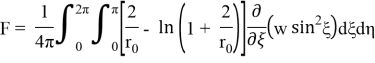
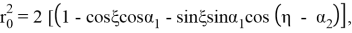
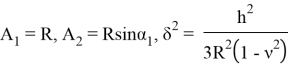
Решение уравнения (1.10), удовлетворяющее граничным условиям, представим в виде
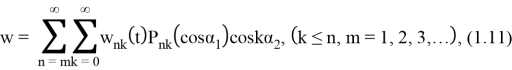
где
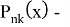
Подставляя (1.11) в уравнение (1.10) и используя процесс ортогонализации, для определения
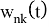
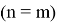
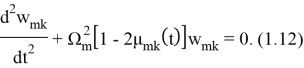
Здесь
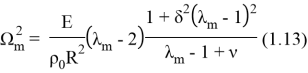
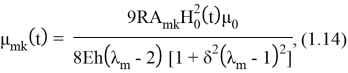
где
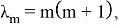
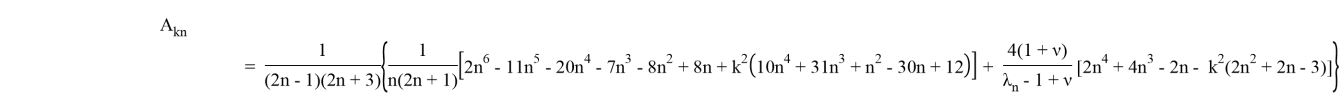
Рассмотрим случай
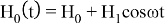
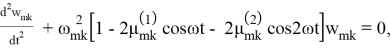
где
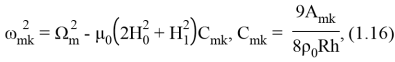
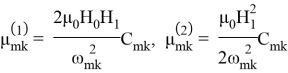
В (1.16)
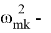
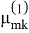
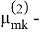
Статическая неустойчивость:
Если оболочка находится в постоянном магнитном поле
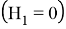
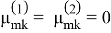
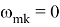
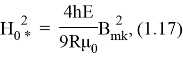
где
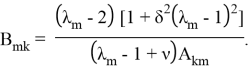
Критическое значение
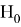
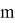
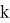
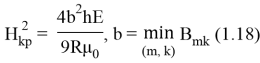
Динамическая неустойчивость:
Уравнение (1.15) представляет собой известное уравнение Матье-Хилла [2]. Его решение может быть неустойчивым, устойчивым или периодическим в зависимости от значений параметров
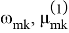
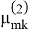
для области, расположенной вблизи частоты
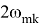
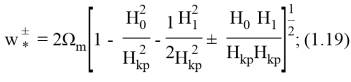
для области, расположенной вблизи частоты
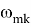
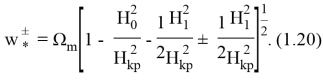
Используя формулы (1.19)-(1.20) легко определить критические параметры напряженности внешнего магнитного поля, под действием которого или происходит потеря статической устойчивости оболочки, или в оболочке возбуждаются резонансные колебания параметрического типа.
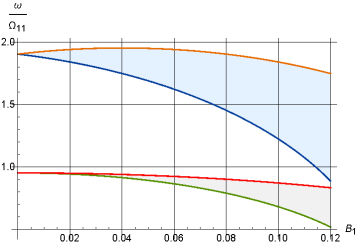
Литература:
- Baghdasaryan G., Mikilyan M. Effects of Magnetoelastic Interactions in Conductive Plates and Shells. Springer, ISBN 978–3-319–19161–4, 2016, -289p.
- Mikilyan M., Marzocca P. Dynamic instability of of electroconductive cylindrical shell in a magnetic field. International Journal of Solids and Structures, 2018, 160, 168–179.

