В современном российском обществе в связи с введением единого государственного экзамена стал весьма актуальным вопрос наиболее быстрой и эффективной подготовки к нему. Эта проблема волнует не только родителей и школьников, но педагогов и методистов. С первых лет проведения данного заключительного испытания основной школы разрабатываются меры интенсивного «подтягивания» обучающихся. Очевидно, что подготовка к государственной итоговой аттестации требует четко организованного системного повторения изученного материала и более глубокого усвоения отдельных тем. Обычно особую трудность ученики испытывают при решении заданий повышенного уровня, поскольку их отличает ярко выраженный нестандартный характер [5, с.845].
Материал, необходимый для построения верного решения, может относиться к различным разделам школьного курса математики, например, неравенства и системы неравенств. Решение неравенств тривиальными алгебраическими методами вызывает у обучающихся ряд трудностей вычислительного характера. Также некоторые сложности могут возникать и при использовании метода интервалов. Для расширения возможностей применения метода интервалов при решении неравенств используем принцип рационализации, известный в математике как метод декомпозиции (Моденов В. П.) или метод замены множителей (Голубев В. И.). Он заключается в замене сложного выражения F(x) на более простое выражение G(x) (в конечном счете, рациональное), при которой неравенство G(x) ˅ 0 равносильно неравенству F(x) ˅ 0 в области определения выражения F(x).
Выделим некоторые выражения F и соответствующие им рационализирующие выражения G (рис.1), где q, p, h, g, f — выражения с переменной x; (h > 0; h ≠ 1; f > 0; g > 0), a — фиксированное число (a > 0; a ≠ 1) [4].

Рис. 1. Соответствующие выражению F рационализирующие выражения G [4]
Рассмотрим следствия, выделенные с учетом области определения функций:
-
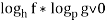
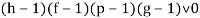
-
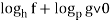
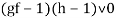
-
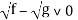
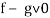
-
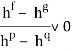
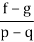
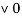
-
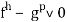
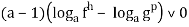 [4].
[4].
Замечание: в указанных равносильных переходах символ ![]() заменяет один из знаков неравенств: >, <, ≤, ≥.
заменяет один из знаков неравенств: >, <, ≤, ≥.
В школьной практике при решении сложных неравенств из банка ЕГЭ эффективнее всего применять именно метод рационализации, поскольку он позволяет избегать двух традиционных ситуаций, где при анализе второй требуется дублировать выкладки из первой (например, выполнять преобразования, осуществлять поиск корней вспомогательных уравнений, определять промежутки монотонности функции). Рассмотрим непосредственное применение метода рационализации на примерах реальных заданий единого государственного экзамена профильного уровня.
Пример 1. Решите неравенство: ![]() . [2]
. [2]
Решение: применяя метод рационализации, приведем неравенство к системе (рис.2):
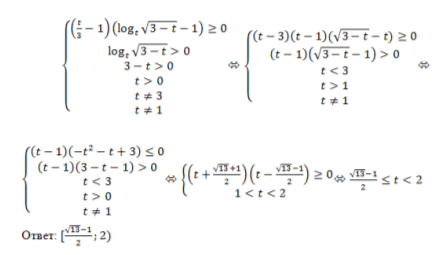
Рис. 2. Решение примера 1
Пример 2. Решите неравенство:
![]() [1, с.58].
[1, с.58].
Решение. Учитывая, что ![]() , получаем:
, получаем:
![]()
![]()
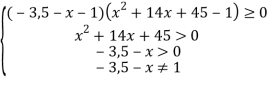
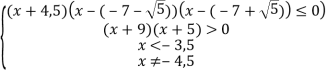
Для выяснения взаимного расположения точек на числовой прямой, сравним числа:
![]() < -9
< -9
![]() > -5
> -5
![]() < -4,5
< -4,5
На рис. 3 на числовой оси показано решение первого неравенства системы:
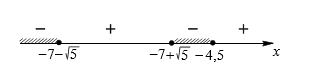
Рис. 3. Решение первого неравенства системы (пример 2)
На рис.4 на числовой оси показано решение всей системы:
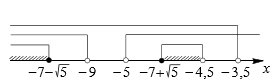
Рис. 4. Решение всей системы (пример 2)
Таким образом, запишем ответ: ![]() .
.
Вышеперечисленные свойства метода рационализации экономят время, и упрощают процесс решения и показательных неравенств, так как позволяют исключать работу с двумя тривиальными случаями. В первом основание положительно, но меньше единицы — знак неравенства обращается. Во втором случае основание больше цифры 1 и, следовательно, знак остается неизменным. Рассмотрим это на примере 3.
Пример 3. Решите неравенство: ![]() [3].
[3].
Построение решения осуществляется на основе системы неравенств:
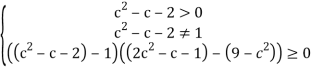
Решив два первых неравенства, найдем ОДЗ:
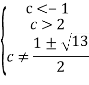
Откуда областью допустимых значений является множество:
![]() ⋃
⋃ ![]() ⋃ c >
⋃ c > ![]() .
.
Далее рассмотрим основное неравенство:
![]() , которое упростим. Получаем:
, которое упростим. Получаем:
![]() . Корни первого множителя соответствующего уравнения равны
. Корни первого множителя соответствующего уравнения равны ![]() , а второго
, а второго ![]() и
и ![]() . Упорядочим корни. Поскольку
. Упорядочим корни. Поскольку
![]() , то
, то ![]() . С помощью метода интервалов получаем решение основного неравенства:
. С помощью метода интервалов получаем решение основного неравенства: ![]() ⋃
⋃ ![]() ⋃
⋃ ![]() . Учитывая ОДЗ, запишем ответ:
. Учитывая ОДЗ, запишем ответ: ![]() ⋃
⋃ ![]() ⋃ c >
⋃ c > ![]() .
.
Метод рационализации возможно применить и для решения систем неравенств. Продемонстрируем данный факт на следующем задании.
Пример 4. Решите систему неравенств: 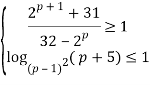 [2].
[2].
Решение. Для данных неравенств запишем ОДЗ. Для первого ![]() , для второго
, для второго ![]() и
и ![]() , а также учитываем многочлен под знаком логарифма
, а также учитываем многочлен под знаком логарифма ![]() . Составим систему неравенств для нахождения ОДЗ (рис.5):
. Составим систему неравенств для нахождения ОДЗ (рис.5):
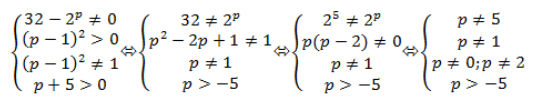
Рис. 5. Система неравенств для нахождения ОДЗ (пример 4)
Приступаем к решению системы неравенств. Неравенство с логарифмами заменяем на произведение ![]() , а второй множитель — разность аргумента большего и меньшего логарифмов. Для этого представим в виде
, а второй множитель — разность аргумента большего и меньшего логарифмов. Для этого представим в виде ![]() . Получим
. Получим ![]() . На основании теоретических сведений о методе рационализации запишем второй множитель
. На основании теоретических сведений о методе рационализации запишем второй множитель ![]() . Подставим в систему неравенств и продолжим решение (рис.6):
. Подставим в систему неравенств и продолжим решение (рис.6):
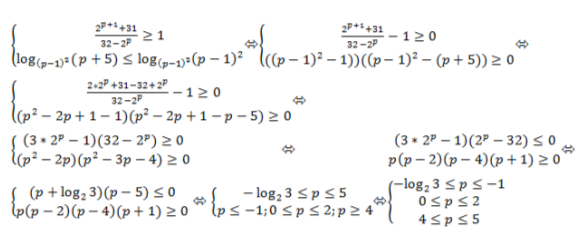
Рис. 6. Решение системы неравенств после подстановки (пример 4)
В итоге, учитывая ОДЗ, получаем ответ исходной системы неравенств:
![]() .
.
Таким образом, решение нестандартных неравенств сопряжено со многими техническими сложностями, что чревато как логическими, так и вычислительными ошибками. Применение тривиальных способов решения неравенств зачастую затруднительно либо невозможно. Метод рационализации позволяет избежать нежелательных осложнений и ошибок, ускорить процесс решения неравенств, что способствует наиболее качественной и эффективной подготовке к единому государственному экзамену.
Литература:
- ЕГЭ. Математика: типовые экзаменационные варианты / Под. ред. И. В. Ященко. — М.: «Национальное образование», 2015. — С.79
- Метод рационализации при решении показательных и логарифмических неравенств / [Электронный ресурс]. — Режим доступа: http://khpms.khspu.ru/wp-content/uploads/kr_2_m_11_12.doc (дата обращения: 26. 03. 17)
- Открытый банк заданий ЕГЭ / [Электронный ресурс]. — Режим доступа: http://www.fipi.ru/content/otkrytyy-bank-zadaniy-ege (дата обращения: 23. 03. 17)
- Подготовка к ЕГЭ по математике 2016. Профильный уровень. Методические указания / [Электронный ресурс]. — Режим доступа: http://roditeli.club/knigi-dlya-detej/podgotovka-k-ege-po-matematike-2016-profilnyj-uroven-metodicheskie-ukazaniya-pdf/ (дата обращения: 22. 03. 17)
- Соловьева О. А., Медведева Я. С. Применение специальных задач для успешного выполнения заданий повышенного уровня единого государственного экзамена // Молодой ученый. — 2016. — № 2. — С. 845–849.

