Оптимальные способы решения квадратных уравнений



Проблема: Решение квадратных уравнений нерациональным способом. Изучив данную тему в 8 классе, учащиеся в старших классах забывают и порой не видят неполные квадратные уравнения и решают их как полные квадратные уравнения, а на это тратится гораздо больше времени. А это потеря времени существенна при сдаче экзамена по математике в форме ЕНТ.

Цель: Изучить различные способы решения квадратных уравнений и отобрать среди них самые оптимальные и быстрые способы решения квадратных уравнений.

Объект исследования: квадратные уравнения.

Еще в Древнем Вавилоне около 2000 лет до н. э. умели решать квадратные уравнения. Необходимость решать их возникла, когда нужно было решать задачи, связанные с нахождением площадей земельных участков. Правила решения вавилонян по существу совпадают с современными, только их решения даны в виде рецептов, без указания способов их нахождения.

В Древней Индии, в 7-ом веке индийский ученый Брахмагупта изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме: ax² + bx = c, a >0; в этом уравнении коэффициенты, кроме а, могут быть и отрицательными. Его правило совпадает с настоящим правилом решения квадратных уравнений. Уже в то время в Древней Индии решали задачи, приводимые к составлению квадратных уравнений, где использовали метод выделения полного квадрата.

Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х² + bx = c, при всевозможных комбинациях знаков коэффициентов b,c было сформулировано в Европе лишь в 1544 г. М.Штифелем.

Всем известная теорема Виета была сформулирована впервые в 1591 г., однако он не признавал отрицательных чисел и при решении уравнений рассматривал лишь случаи, когда все корни положительны. Однако символика Виета была далека от современного вида. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Определение. Квадратным называется уравнение вида: ax² +bx + c = 0, a 0, в котором х – переменная, а,b,с – любые числа.

Числа а и b называются первым и вторым коэффициентами, а число с – свободным членом квадратного уравнения.

В школьном курсе математики изучаются следующие способы решения квадратных уравнений:

1. Решение с помощью формул корней квадратного уравнения. 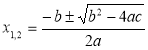Таким способом можно решать любые квадратные уравнения.

2. Если второй коэффициент b = 2k – четное число, то формулу корней можно записать в виде: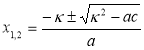

3. Решение с помощью теоремы Виета, с ее помощью решаются квадратные уравнения с целыми корнями (а = 1), эти корни без труда находятся подбором.

В настоящее время можно привести еще несколько способов решения квадратных уравнений:

4. Способ разложения левой части на множители.

Например: Решим уравнение:

Левую часть уравнения разложим на множители:

.

Таким образом уравнение запишется так:

. Произведение двух множителей равно нулю тогда только тогда, когда один из множителей равен нулю, т. е. или , отсюда x= -10 , или x = 2.

5. Способ выделения полного квадрата

Например: Решить уравнение:

.

x₁=1, или x+3=-4, x₂=-7.

6. Решение квадратных уравнений с помощью циркуля и линейки.

Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.

Предлагаю следующий способ нахождения корней квадратного уравнения с помощью циркуля и линейки.

Допустим, что искомая окружность пересекает ось абсцисс в точках B(x₁;0) и D(x₂;0), где x₁ и x₂ – корни уравнения , и проходит через точки A(0;1) и C(0;c/a) на оси ординат. Тогда по теореме о секущих имеем OB • OD= OA • OC, откуда OC= OB • OD/OA= x₁x₂/ 1= c/a

Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD

итак:

1) Построим точки (центр окружности) и A(0;1);

2) Проведем окружность с радиусом SА;

3) Абсцисс точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.

7. Решение квадратных уравнений с помощью номограммы.

Этот старый и забытый способ решения квадратных уравнений.

Номограмма для решения уравнения z²+pz+q=0. Эта номограмма позволяет не решая квадратного уравнения, по его коэффициентам определить корни уравнения. Криволинейная шкала номограммы построена по формулам.

8. Геометрический способ решения квадратных уравнений.

В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» Аль-Хорезми.

Решим уравнение х²+6х-16=0

х²+6х=16, или х²+6х+9=16+9.

Выражения х²+6х+9 и 16+9 геометрически представляют собой один и тот же квадрат, а исходное уравнение х²+6х-16+9-9=0 – одно и то же уравнение. Откуда и получаем, что х+3=±5, или х₁=2, х₂=-8

9. Решение квадратных уравнений с помощью теоремы Виета становится уже практически неприменимым, если уравнение имеет дробные корни. Для преодоления озникшей трудности используется следующий прием: «перебросить» коэффициент а в свободный член (умножить свободный член на а). После этого найти корни нового уравнения и разделить их на а.

Приведем пример. Решить уравнение: 12х² +13х +3 = 0; а= 12,

Таким образом: х² + 13х + 3 · 12 = 0; Теперь свободный член равен 36, по теореме Виета сумма двух корней должна быть равна (-13). Эти числа (-4) и (-9). Тогда разделив их на 12, получим, что корни исходного уравнения:

10. Способ использования свойств коэффициентов.

Пусть дано квадратное уравнение ax2 +bx +c =0 .

а) Если а+ b+с = 0 (то есть сумма коэффициентов уравнения равна нулю), то

Например. Решить уравнение 345 х2 – 137х -208 =0. Т. к. 345-137-208=0, то

б) Если a - b+c=0 или b=a+c , то

Например. Решим уравнение: 11 х² +27х +16 = 0, так как, 11+16 =27, то

При решении показательных, логарифмических, тригонометрических, иррациональтных, биквадратных и др. уравнений используются квадратные уравнения. Многие текстовые задачи решаются составлением квадратных уравнений. Подводя итоги, можно сделать вывод: квадратные уравнения играют огромную роль в развитии математики. Способов решения их очень немало. Приведенные же способы решения квадратных уравнений специального вида позволяют очень быстро и рационально решать многие уравнения. Умение быстро находить корни квадратного уравнения имеет большое значение при тестировании и сдаче экзаменов. Знание способов быстрого решения квадратных уравнений может пригодиться нам на притяжении всей жизни. Эти методы решения квадратных уравнений просты в применении и они, безусловно, должны заинтересовать увлекающихся математикой учеников.

Литература:

1. Глейзер Г.И. История математики в школе. – М.: Просвещение, 1982.
2. Гусев В.А., Мордкович А.Г. Математика: Справочные материалы: Книга для учащихся, – М.: Просвещение, 1988.
3. Окунев А.К. Квадратные функции, уравнения и неравенства.
4. Рустюмова И.П., Рустюмова С.Т. Пособие для подготовки к ЕНТ по математике. – Алматы, 2010. – 716 с.