В статье автор рассматривает применение некоторых нестандартных методов с целью оптимизации решения уравнений и неравенств. Представляется созданный автором уникальный онлайн-тренажер как способ самостоятельной подготовки к решению уравнений и неравенств, представленных, в том числе, в заданиях ЕГЭ.
Для успешной сдачи ЕГЭ очень важно правильно распределять и экономить время, поэтому требуются новые методы решения, обеспечивающие наиболее быстрое выполнение заданий.
На уроках математики в школе изучаются такие методы решения уравнений и неравенств, как: разложение на множители, замена переменной, схема Горнера, теорема Безу, теорема Виета, метод интервалов и др. Однако их применение не всегда обеспечивают быстроту решения и минимальность ошибок. Это обуславливает необходимость в поиске методов решения уравнений и неравенств, позволяющих сократить количество шагов решения в алгоритме и снизить вероятность допущения ошибки.
К числу таких методов относятся: метод рационализации, учет ОДЗ, метод мажорант (метод оценки), использование свойств функции, графиков функций, угадывание корня.
Метод рационализации
(метод декомпозиции, метод замены множителей) заключается в замене сложного выражения
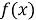
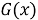
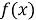
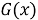
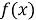
Приведем алгоритм решения уравнений и неравенств методом рационализации :
- Нахождение ОДЗ уравнения/неравенства.
- Привести данное неравенство к стандартному виду: слева дробь (или произведение), справа — ноль.
- Заменить выражения левой части на более простые, эквивалентные им по знаку.
- Решить полученное неравенство, например, методом интервалов.
Ниже приведена таблица наиболее часто встречающихся замен:

Раскроем применение составленного нами алгоритма при решении неравенства
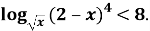
- Определим ОДЗ неравенства:
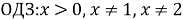
- Приведем логарифмы к одному основанию:
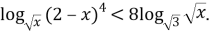
- Упростим выражение. Для этого воспользуемся формулой
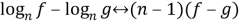
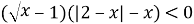
Отсюда
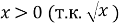
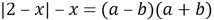
-
Продолжаем упрощение с помощью формулы
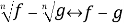
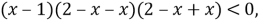
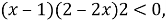
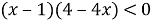
- Сравним каждый множитель левой части неравенства с нулём:
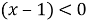
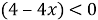
- Решим каждое неравенство:
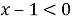
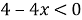
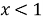
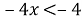
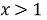
- Используем метод интервалов с учетом ОДЗ:
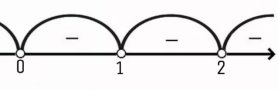
Отсюда
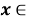
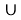
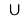
Учёт ОДЗ . Иногда знание ОДЗ позволяет доказать, что уравнение (или неравенство) не имеет решений, а иногда позволяет найти решение уравнения (или неравенства) непосредственно подстановкой чисел из ОДЗ.
Приведём алгоритм решения уравнений и неравенств методом учёта ОДЗ :
- Найти ОДЗ уравнения/неравенства.
- Подставить значение ОДЗ в исходное уравнение/неравенство, чтобы проверить, является ли оно корнем.
Покажем
решение уравнения
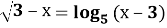
Для этого найдём ОДЗ уравнения: оно состоит из всех х, одновременно удовлетворяющих условиям
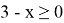
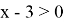
Метод мажорант также называют методом оценки левой и правой частей, входящих в уравнения и неравенства.
Мажорантой данной функции f(х) на множестве Р , называется такое число М , что либо f(х) ≤ М для всех х ϵ Р , либо f(х) ≥ М для всех х ϵ Р .
Мажоранты многих элементарных функции известны. Их нетрудно указать, зная область значений функции.
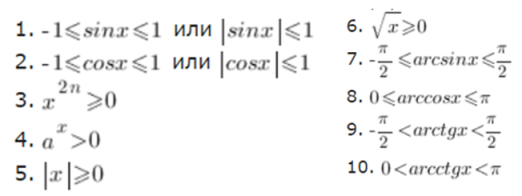
Алгоритм решения указанного метода состоит из следующих шагов:
- Оценить левую часть уравнения/неравенства.
- Оценить правую часть.
- Составить систему уравнений/неравенств.
- Решить систему и сделать вывод.
- Выполнить проверку.
- Записать ответ.
Покажем применение алгоритма при решении такого уравнения
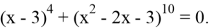
- Оценим левую и правую части уравнения:
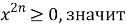
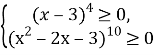
Так как левая часть уравнения приравнивается к нулю, то равенство возможно только в том случае, если оба слагаемых равны нулю.
- Составим систему уравнений:
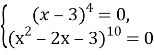
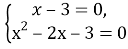
- Решим систему уравнений:
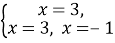
- Выполним проверку:
При
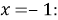
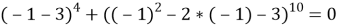
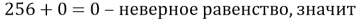
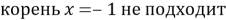
При
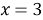
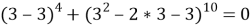
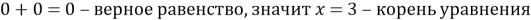
Использование монотонности функции.
Утверждение 1
. Если функция
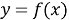
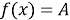
Утверждение 2.
Если функция
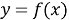
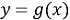
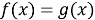
С помощью утверждений 1 и 2 можно обосновать единственность решения уравнения в тех случаях, когда решить его стандартными способами не представляется возможным, но при этом удается подобрать корень уравнения, который, как правило, является целым числом. При этом надо учитывать, что решение уравнения «методом подбора» не будет засчитано при проверке без обоснования того, что уравнение не имеет других корней. Такое обоснование часто удается сделать, опираясь на свойства монотонности функций.
Приведём алгоритм решения уравнений и неравенств методом использования монотонности функции:
- Определить монотонность и область определения функции (ООФ).
- Методом подбора найти корень уравнения/неравенства.
- Исходя из монотонности функции делаем вывод о количестве корней.
При
решении уравнения
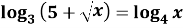
- Воспользуемся методом замены:
Пусть
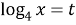
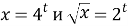
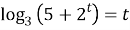
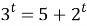
- Определим монотонность функций:
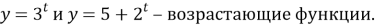
-
Методом подбора находим корень
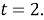
-
Разделим обе части уравнения на
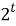
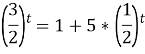
- Снова определим монотонность полученных функций:
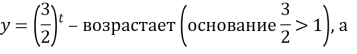
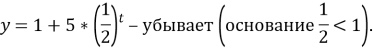
Отсюда следует, что
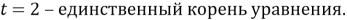
- Вернемся к замене:
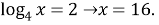
Использование графиков функции. При решении уравнений и неравенств иногда полезно рассмотреть эскиз графиков их правой и левой частей. Тогда этот эскиз графиков поможет выяснить, на какие множества надо разбить числовую ось, чтобы на каждом из них решение уравнения (или неравенства) было очевидно.
Обратим внимание, что эскиз графика лишь помогает найти решение, но писать, что из графика следует ответ, нельзя, ответ ещё надо обосновать.
Приведём алгоритм решения уравнений и неравенств с помощью использования графиков:
- Определить ОДЗ уравнения/неравенства.
- Представить левую и правую части уравнения/неравенства как
функции и построить их графики.
- По графику определить решение уравнения/неравенства.
- Доказать справедливость ответа.
Применим построенный алгоритм при решении неравенства
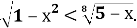
- Определим ОДЗ неравенства:
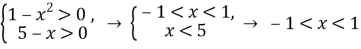
-
Представим функции
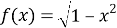
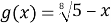
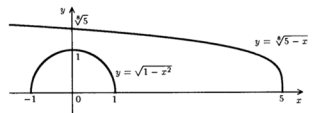
Из рисунка следует, что для всех х из ОДЗ исходное неравенство справедливо.
- Докажем справедливость ОДЗ:
При
х ∈ [-1;1]:
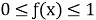
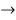
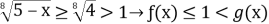
Значит, решениями исходного неравенства будут все х из промежутка [-1;1].
Угадывание корня уравнения (искусственный метод решения уравнений). Иногда внешний вид уравнения подсказывает, какое число является корнем уравнения.
Раскроем алгоритм решения уравнений методом угадывания корня :
- Методом подбора определить корень уравнения.
- Найти ОДЗ уравнения.
- Привести многочлен к стандартному виду.
- Определить остальные корни уравнения.
При решении уравнения
:
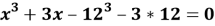
- Методом подбора определим корень уравнения:
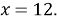
- Приведём многочлен к стандартному виду:
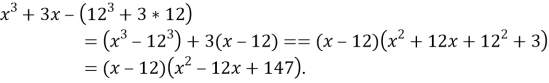
- Найдём остальные корни:
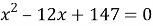
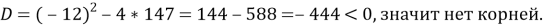
Отсюда следует, что
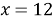
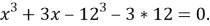
В качестве проектного продукта проведенного исследования был выбран интерактивный тренажер, который позволит практиковаться в решении уравнений и неравенств с помощью новых, нестандартных методов решения. Размещение тренажера на сетевой платформе позволит сделать данный продукт доступным для всех, кто хочет разобраться в этой теме.
В таблице ниже приведены результаты оценки сетевых сервисов по выбранным критериям:
|
Сетевой сервис |
Критерии оценивания | ||
|
Интерфейс |
Разнотипность |
Мобильная версия | |
|
Quizizz |
+ |
- |
+ |
|
Wordwall |
+ |
+ |
+ |
|
PurposeGames |
+ |
+ |
+ |
|
Wizer.me |
+ |
+ |
+ |
|
LearningApps |
+ |
+ |
+ |
|
Сетевой сервис |
Критерии оценивания | ||
|
Русский |
Бесплатность |
Доступность | |
|
Quizizz |
- |
+ |
+ |
|
Wordwall |
+ |
- |
+ |
|
PurposeGames |
- |
+ |
+ |
|
Wizer.me |
- |
+ |
+ |
|
LearningApps |
+ |
+ |
+ |
В результате сравнения сетевых сервисов по указанным критериям для создания интерактивного тренажера была выбрана платформа LearningApps, которая соответствует наибольшему количеству требований.
В процессе размышления над идеей контента тренажёра было принято решение представить продукт, объединив теорию и тренажёры (упражнения) в одну презентацию.
Презентация. Основная задача презентации заключается в наглядном представлении алгоритмов решения уравнений/неравенств, примеров решения, а также в размещении ссылок на онлайн-тренажёры для каждого метода.
Тренажёр. Для каждого метода решения уравнений/неравенств создано несколько тренажёров (упражнений): на проработку алгоритма, проработку ключевых формул (если такие имеются) и на тренировку самого решения.
Доступ к тренажеру обеспечивается ссылкой https://infourok.ru/prezentaciya-po-algebre-na-temu-nekotorye-nestandartnye-metody-resheniya-uravnenij-i-neravenstv-9–11-klass-5183275.html и QR кодом.

В ходе создания продукта была выбрана концепция тренажёра, позволяющая объединить теорию и практику. Апробация показала, что изучение некоторых нестандартных методов решения уравнений и неравенств становится более наглядным и структурированным. Создание такого информативного, эффективного, удобного в использовании и общедоступного тренажера позволяет решить проблему увеличения скорости решения и минимизации ошибок.
Считаем необходимостью изучение рассмотренных методов, ведь они в действительности являются незаменимыми при решении уравнений и неравенств.
Литература:
- Олехник С. Н., Потапов М. К., Пасиченко П. И. Уравнения и неравенства. Нестандартные методы решения: справочник. 1997. — 219 с.
- Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: базовый и углубленный уровни. 7-е изд. М.: Просвещение, 2019. — 384 с.
- Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин. Математика: алгебра и начала математического анализа. 11 класс: базовый и профильный уровни. 2-е изд. М.: Просвещение, 2010. — 336 с.
- Образовательный портал для подготовки к экзаменам. Сдам ГИА: Решу ЕГЭ. ЕГЭ — 2021, Математика профильного уровня: задания, ответы, решения. Обучающая система Дмитрия Гущина. Задания: № 13, № 15.

