Рассматриваются вопросы линеаризации уравнений динамики при решении актуальных задач, связанных с разработкой тренажных и обучающих комплексов для подготовки операторов человеко-машинных систем. Приводятся иллюстрации на конкретных примерах.
Ключевые слова:эргатические системы, приближенные методы решения уравнений динамики, линеаризация, оценка точности.
Для успешного и быстрого решения многих задач, возникающих при разработке эргатических систем необходимы эффективные и удобные в применении методы анализа и расчета процессов, протекающих в линейных системах. Непрерывные линейные системы могут быть как стационарными, так и нестационарными. Изучение нестационарных систем связано с большими трудностями математического характера. Дифференциальные уравнения с переменными коэффициентами не интегрируются в квадратурах; возникает необходимость использования приближенных методов. Трудности несоизмеримо возрастают при переходе к вероятностным задачам.
Линейные системы в практических приложениях встречаются значительно редко, значительно чаще — системы непрерывного действия, линейные в малом. Такие системы допускают линеаризацию с заданной точностью уравнений динамики в малой окрестности какой-либо фазовой траектории движения (параметрической кривой в n-мерном пространстве). Ограничимся линеаризацией уравнений движения эргатической системы, связанной с разработкой тренажных и обучающих комплексов. Их качественное исследование во многом определяется численным решением начальной задачи для нелинейной системы
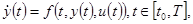
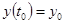 ; (1)
; (1)
траектория объекта управления 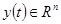 , а управляющее воздействие
, а управляющее воздействие 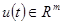 .
.
Предположим, что условия аппроксимации позволяют привести (1) к виду
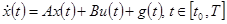
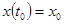 ; (2)
; (2)
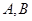 — некоторые постоянные матрицы,
— некоторые постоянные матрицы, 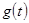 — некоторая функция.
— некоторая функция.
Если функция 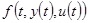 почти линейная по
почти линейная по 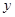 и
и 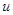 и стационарна, то можно ожидать близость движений этих систем (теоремы о непрерывной зависимости решений системы от параметров и возможности линейной аппроксимации непрерывных функций).
и стационарна, то можно ожидать близость движений этих систем (теоремы о непрерывной зависимости решений системы от параметров и возможности линейной аппроксимации непрерывных функций).
Однако заметим, указанные теоремы обосновывают лишь локальную аппроксимацию (на этом основаны многие достаточно надежные численные методы решения дифференциальных уравнений). Непрерывную функцию можно аппроксимировать (с требуемой точностью) линейной только в достаточно малой окрестности; при глобальной аппроксимации погрешности могут быть и значительными (с увеличением размерности системы погрешности могут возрастать).
Имеем:
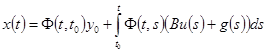 ,
,
здесь 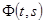 — фундаментальная матрица решения системы
— фундаментальная матрица решения системы
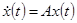 ,
,
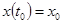 ;
;
ее столбцы 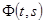 имеют вид
имеют вид
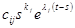 ,
,
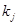 — натуральные числа, не превосходящие кратности соответствующих собственных чисел
— натуральные числа, не превосходящие кратности соответствующих собственных чисел 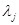 матрицы A.
матрицы A.
Погрешность решений задач (1) и (2) можно оценить по изменению характеристических чисел 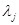 при изменении коэффициентов матрицы A (при глобальной аппроксимации матрица A определяется правой частью системы (1) неоднозначно). В частности, для системы второго порядка собственные числа
при изменении коэффициентов матрицы A (при глобальной аппроксимации матрица A определяется правой частью системы (1) неоднозначно). В частности, для системы второго порядка собственные числа 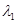 и
и 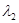 определятся из
определятся из
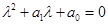 ;
;
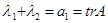 ,
, 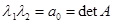 .
.
Если
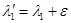 ,
,
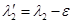
(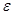 может быть как действительным, так и комплексным), то
может быть как действительным, так и комплексным), то 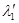 и
и 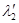 — собственные числами другой матрицы
— собственные числами другой матрицы 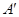 . Так как
. Так как 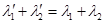 , то:
, то:
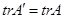 , (3)
, (3)
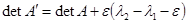 . (4)
. (4)
Заметим, даже при практическом совпадении матриц 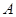 и
и 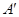 (значение
(значение 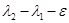 мало) их собственные числа (ими определяются поведения решений) могут существенно отличаться. Например, при
мало) их собственные числа (ими определяются поведения решений) могут существенно отличаться. Например, при
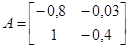 ,
, 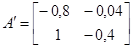
матрицы 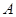 и
и 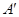 отличаются лишь одним коэффициентом (
отличаются лишь одним коэффициентом (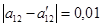 ); их собственные числа отличаются по модулю на 0,1 (
); их собственные числа отличаются по модулю на 0,1 (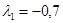 ,
,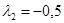 ;
; 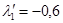 ,
,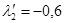 ). При этом общие решения
). При этом общие решения
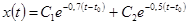 ,
,
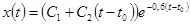
однородных систем с матрицами 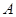 и
и 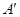 отличаются даже по структуре.
отличаются даже по структуре.
А в случае
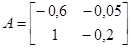 ,
, 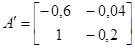
характеристические уравнения соответственно имеют вид
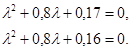 ,
,
Корни этих уравнений:
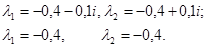
Как видим, незначительное изменение 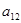 (всего на 0,01) приводит колебательную систему уже к апериодической.
(всего на 0,01) приводит колебательную систему уже к апериодической.
Таким образом, аппроксимация уравнений движения человеко-машинной системы «оператор-объект управления» линейной системой во многих случаях является возможной, но требует проверки в каждом конкретном случае. Однако в большинстве случаев при практическом синтезе может использоваться в качестве нулевого приближения. Такой подход использовался при синтезе ряда транспортных эргатических систем [1…5].
Литература:
1. Родионов Ю. В., Ветохин А. С. Динамический автотренажер / Мир транспорта и технологических машин. — 2011. — № 4. –С.90–93.
2. Гарькина И. А., Данилов А. М., Пылайкин С. А. Тренажеры и имитаторы транспортных систем: выбор параметров вычислений, оценка качества / Мир транспорта и технологических машин. –№ 3(42). –2013. –С.115–121.
3. Будылина Е. А., Данилов А. М., Пылайкин С. А., Лапшин Э. В. Тренажеры по подготовке операторов эргатических систем: состояние и перспективы /
4. Современные проблемы науки и образования. –2014. — № 4. — С. 154.
5. Гарькина И. А., Данилов А. М., Пылайкин С. А. Транспортные эргатические системы: информационные модели и управление / Мир транспорта и технологических машин. — 2013. — № 1 (40). — С. 113–120.
6. Гарькина И. А., Данилов А. М., Прошин И. А. Тренажеры модульной архитектуры для подготовки операторов транспортных систем / XXI век: итоги прошлого и проблемы настоящего (плюс) Серия: технические науки. Машиностроение и информационные технологии. — № 12(16). — 2013. –С. 37–42.

