Определяются основные неопределенности в описании динамических систем в рамках линейных математических моделей; приводится метод их эффективной оценки, прошедшие практическую апробацию.
Ключевые слова:динамические системы, линейные модели, учет неопределенностей, оценка параметров.
При решении большинства практических задач (виброзащита, сейсмостойкость, мониторинг конструкций и сооружений, эргатические системы и др. [1,2]) при проектировании требуются эффективные, удобные в применении и доступные инженерные методы анализа и расчета процессов, протекающих в линейных процессах. Наибольшую трудность представляют собой анализ и синтез нестационарных систем. Прежде всего, трудности математического характера: дифференциальные уравнения с переменными коэффициентами не интегрируются в квадратурах; необходимость использования методов приближенных вычислений. Неизмеримо эти трудности возрастают при переходе к вероятностным задачам. В связи с большим разнообразием решаемых задач актуальной является разработка единого подхода к рассмотрению как стационарных, так и нестационарных систем в рамках теории непрерывных линейных систем.
При описании линейными моделями объект, хотя бы приближенно, должен быть линейным. Модель описывается некоторым числом параметров. Их значения должны быть выбраны так, чтобы, подавая на вход модели тот же входной сигнал, что и на вход объекта, можно было получить на ее выходе сигнал, отличающийся как можно меньше от того, который наблюдается на выходе объекта. Модель не должна содержать источников шумов, некоррелированных с соответствующими шумами объекта (при усреднении они только увеличат среднеквадратичное значение между выходными сигналами). Предполагается, что имеется информация, содержащаяся в конечных во времени реализациях на входе и выходе, для определения передаточной функции объекта. Так же предполагается, что на выходной сигнал объекта накладывается шум (рис.1,2); источники шума имеются как в самом объекте, так и в измерительных приборах.

Рис.1. Структура сигналов в реальной системе: 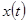 - входной сигнал объекта,
- входной сигнал объекта, 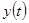 - неслучайная часть выходного сигнала,
- неслучайная часть выходного сигнала, 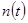 — случайная часть выходного сигнала
— случайная часть выходного сигнала
Разность между выходными сигналами реальной системы и модели определится в виде
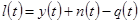 .
.
Передаточная функция модели 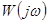 определяется параметрами
определяется параметрами 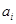 .
.
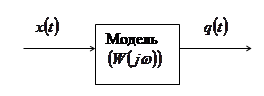
Рис.2. Линейная модель: 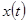 - входной сигнал,
- входной сигнал, 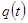 — выходной сигнал
— выходной сигнал
После подстройки параметров получается наилучшая из практически реализованных моделей. Естественно, модель не будет абсолютно точной: помехи и конечность времени наблюдения сделают ее параметры до некоторой степени неопределенными. Поэтому актуальны оценка неопределенности произвольного параметра и получение аналитических зависимостей, связывающих неопределенность параметров с основными факторами при решении задачи синтеза модели. Эти зависимости могут использоваться для ответа на вопросы:
- каким должен быть период наблюдения для получения заданной точности модели;
- при каких входных сигналах достигается наименьшая неопределенность в значениях параметров?
Что же касается природы входного сигнала, то на этом этапе никакие специальные предположения не требуются.
Если этот сигнал записан и, таким образом, полностью известен, то не важно, генерируется он детерминированным или случайным источником. Можно показать, для случайных сигналов на входе объекта не требуется записей отдельных реализаций, а достаточно знать статистические характеристики источника этих сигналов. В качестве меры неопределенности значения параметра естественно принять среднеквадратичное значение дисперсии параметра 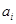 :
:
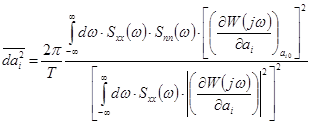 .
.
Здесь:
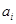 -i-й параметр в передаточной функции модели
-i-й параметр в передаточной функции модели 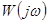 ;
;
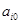 - значение параметров
- значение параметров 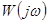 , при которых модель и объект оказываются идентичными (фактически определенные значения параметров
, при которых модель и объект оказываются идентичными (фактически определенные значения параметров 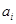 );
);
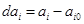 - отклонения параметров;
- отклонения параметров;
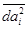 - среднеквадратичное значение дисперсии параметра,
- среднеквадратичное значение дисперсии параметра,
 - спектральная плотность
- спектральная плотность  ;
;
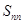 - спектральная плотность
- спектральная плотность 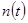 .
.
Как видим:
- входной сигнал 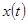 должен быть мощным и, насколько это возможно, лежать в частотном диапазоне, определяемом функцией влияния параметра;
должен быть мощным и, насколько это возможно, лежать в частотном диапазоне, определяемом функцией влияния параметра;
- выходной шум должен быть слабым и, по возможности, находиться вне указанного выше диапазона.
- предпочтительнее пользоваться большим временем наблюдения 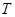 (неопределенность обратно пропорциональна квадратному корню из
(неопределенность обратно пропорциональна квадратному корню из 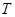 ).
).
Непосредственно из предыдущего вытекает необходимость:
- математического определения понятия непрерывной линейной системы (с сосредоточенными параметрами и классификация процессов, протекающих в системе),
- преобразования исходной системы уравнений динамики к видам, удобным для расчета и анализа процессов (в том числе, к одному линейному дифференциальному уравнению (порядок совпадает с порядком исходной системы)),
- разработки методов определения характеристик линейной (как колебательной, так и апериодической) системы; свободные колебания стационарных систем могут определяться на базе обобщенного характеристического уравнения.
Что касается вынужденных колебаний, то при их исследовании, как правило, сложность решения зависит от того, являются ли они следствием детерминированных или случайных воздействий. Наиболее сложный класс представляют собой системы со случайными параметрами.
Указанные вопросы наиболее четко проявились и успешно решались при анализе и синтезе транспортных систем (в том числе при разработке комплексов для подготовки операторов [3…6]).
Литература:
1. Прошин А. П., Данилов А. М., Королев Е. В., Смирнов В. А. Динамические модели при исследовании кластерообразования в композиционных материалах. Предельные системы / Известия высших учебных заведений. Строительство. — 2002. — № 3. -С. 32.
2. Данилов А. М., Гарькина И. А., Гарькин И. Н. Спектральные методы при анализе динамических систем / Региональная архитектура и строительство. — 2014. — № 3. — С. 109–113.
3. Гарькина И. А., Данилов А. М., Прошин И. А. Тренажеры модульной архитектуры для подготовки операторов транспортных систем / XXI век: итоги прошлого и проблемы настоящего плюс. -2013. — № 12 (16). — С. 37–42.
4. Гарькина И. А., Данилов А. М., Пылайкин С. А. Практические методы идентификации транспортных эргатических систем / Альманах современной науки и образования. — 2013. — № 8 (75). — С. 50–52.
5. Гарькина И. А., Данилов А. М., Пылайкин С. А. Имитаторы движения транспортных средств / Альманах современной науки и образования.- 2013. — № 7 (74). — С. 40–42.
6. Тюкалов Д. Е., Данилов А. М. Моделирование и подготовка операторов транспортных эргатических систем / Молодой ученый. — 2015. — № 3 (83). — С. 247–249

