В статье предлагается новый подход к построению систем управления для объектов с неопределенными параметрами в форме трехпараметрических структурно-устойчивых отображений из теории катастроф, позволяющей синтезировать высокоэффективные системы управления, обладающие предельно широкой областью робастной устойчивости. Исследование робастной устойчивости систем управления базируется на новом подходе к пострению функций А. М. Ляпунова. Излагается метод построения системы управления с повышенным потенциалом робастной устойчивости.
Ключевые слова: система управления, неопределенность параметров, робастная устойчивость, структурно-устойчивые отображения, область устойчивости.
I. Введение
Проблема исследования устойчивости занимает одно из центральных мест при создании систем управления техническими объектами и технологическими процессами, которые широко применяются практически во всех сферах производства и техники: в машиностроении, энергетике, электронной, химической, биологической, металлургической и текстильной промышленности, транспорта, робототехнике, авиации, космических системах, высокоточной военной технологии и технике и т. д.
В настоящее время общепризнано, что большинство реальных систем управления функционирует в условиях той или иной степени неопределенности. При этом неопределенность может быть обусловлена незнанием истинных значений параметров объектов управления и непредсказуемым изменением их во времени (в процессе эксплуатации). Поэтому проблема робастной устойчивости является одной из наиболее актуальных в теории управления и представляет большой практический интерес. В общей постановке она состоит в указании ограничений на изменения параметров системы, при которых сохраняется устойчивость. Ясно, что эти ограничения определяются областью устойчивости по неопределенным параметрам объекта и устанавливаемым параметрам устройства управления.
Известные методы [1,2,3,4] построения систем управления объектами с неопределенными параметрами в основном посвящены определению робастной устойчивости системы с заданной структурой с линейными законами управления или безынерционными нелинейными (релейными) характеристиками и не позволяют проектировать системы управления с достаточно широкой областью робастной устойчивости в условиях большой неопределенности параметров объекта управления и дрейфа их характеристики в больших пределах.
В [5] особое внимание уделено динамическим системам, в которых рассматриваются развитие процессов самоорганизации в физико-химических и биологических системах. Модели этих систем представляются в форме структурно-устойчивых отображений из теории катастроф [6,7] и исследуются как универсальная математическая модель развития и самоорганизации в живой природе. В связи с этим представляет определенный интерес в условиях большой неопределенности построить систему автоматического управления в классе структурно-устойчивых отображений с математическими моделями, сопутствующими сложному поведению системы, а именно имеющими множество последовательно устойчивых решений.
Данное исследование посвящено актуальным проблемам построения робастной устойчивой системы управления линейными динамическими объектами с неопределенными параметрами с подходом к выбору законов управления в классе трехпараметрических структурно-устойчивых отображений, позволяющих предельно увеличить потенциал робастной устойчивости и показатели качества системы управления [8,9,10,11,12,13,14].
Концепция построения системы управления с повышенным потенциалом робастной устойчивости динамическими объектами базируется на результатах теории катастроф [6,7], где как основной результат получены важнейшие структурно-устойчивые отображения. Они ограничены и непосредственно определяются числом управляющих параметров. Универсальным методом исследования устойчивости динамических систем является метод функций А. М. Ляпунова [15,16]. В качестве инструмента исследования в методе Ляпунова используются некоторые специальные непрерывно дифференцируемые, обращающие в начале координат в нуль функции, называемые функцией Ляпунова. Применение данного метода сдерживается отсутствием универсального подхода к построению функции Ляпунова. Следует напомнить, что ошибка в выборе и неудача построить необходимую функцию Ляпунова не означает неустойчивости системы: она указывает только на неудачу при построении функций Ляпунова [15,16,17].
В настоящее время отсутствуют универсальные научные положения по разработке и исследованию робастной устойчивости нелинейных систем управления с достаточно широкой областью устойчивости, обеспечивающих наилучшую защиту от развития в системе режима «детерминированного хаоса». Поэтому представляется важным в условиях большой неопределенности в параметрах объектов управления с порождением хаоса, построить систему автоматического управления в классе структурно-устойчивых отображений [6,7] с математическими моделями, сопутствующими сложному поведению системы [8,9,10,11,12,13,14], а именно имеющими последовательно устойчивые решения.
Исследование последних лет показали, что для изучения робастности линейных или нелинейных систем управления с успехом могут применяться методы построения функций А. М. Ляпунова, основанные на геометрической интерпретации теоремы А. М. Ляпунова в пространстве состояний [18,19,20,21].
В статье рассматриваются проблемы построения систем управления с повышенным потенциалом робастной устойчивости с новым подходом к исследованию робастности по методу функций А. М. Ляпунова [18,19,20,21].
II. Математическая формулировка модели
Рассмотрим стационарную замкнутую систему управления с одним входом и одним выходом, описываемую уравнением состояния,
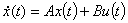(1)
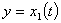
где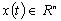 
- вектор состояния объекта; 
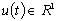— скалярная функция управляющих воздействий; 
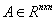— матрица объекта управления с неопределенными параметрами размерности 
, 
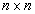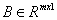— матрица управления размерности 
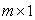. Матрицы 
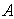и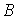 
имеют следующий вид:
, 
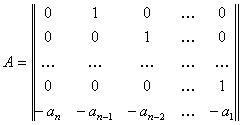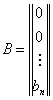
Закон управления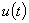 
в замкнутом контуре задан в форме суммы трехпараметрических структурно-устойчивых отображений (катастрофа «гиперболическая омбилика»):
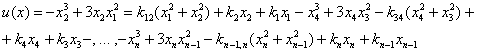(2)
Система (1) в развернутом виде записывается:
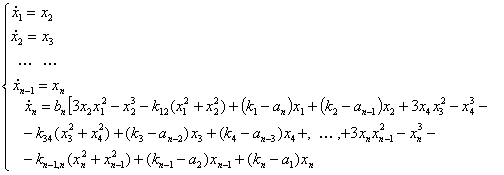(3)
III. Стационарные состояние системы
Стационарные (установившиеся) состояния системы определяются решением уравнения:
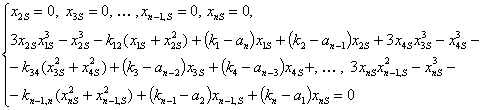(4)
Из уравнения (4) можно получить стационарные состояния, определяемые тривиальным решением системы (4):
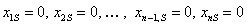(5)
Некоторые другие стационарные состояния будут определяться решением уравнений
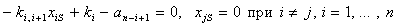(6)
или
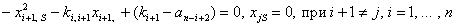(7)
Уравнение (6) имеет следующие решения:
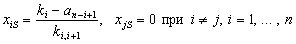(8)
Уравнения (7) при отрицательных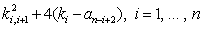 
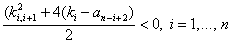имеют мнимые решения, что не может соответствовать какой-либо физически возможной ситуации. При 
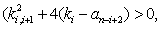уравнение (7) допускает следующие решения:
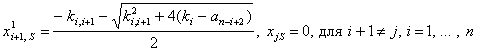(9)
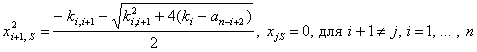(10)
IV. Исследование устойчивости стационарных состояний
Устойчивость стационарных состояний (5), (8), (9) и (10) системы (3) будем исследовать на основе предложенного подхода методам функции Ляпунова.
Рассмотрим устойчивость стационарного состояния (5). Для этого обозначим компоненты вектора антиградиента вектор-функции Ляпунова
…
…
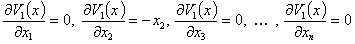
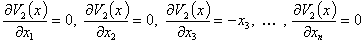
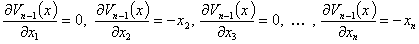
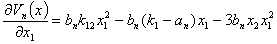
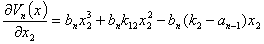
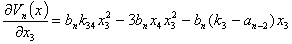
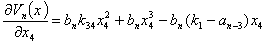
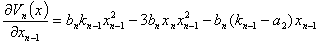
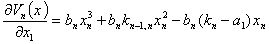
Полная производная по времени от вектор-функций Ляпунова будет равна:
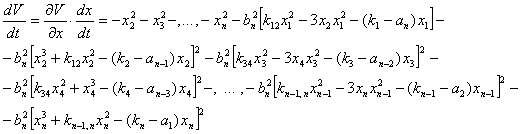(11)
Из (11) получаем, что полная производная по времени от вектор-функций Ляпунова будет знакоотрицательной функцией, следовательно, достаточное условие асимптотической устойчивости системы (3) относительно стационарного состояния (5) выполняется.
По вектору градиента от вектор-функций Ляпунова строим неизвестные компоненты вектор-функций Ляпунова в виде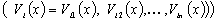 
:
…
…
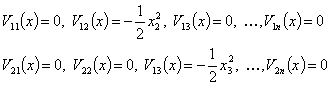
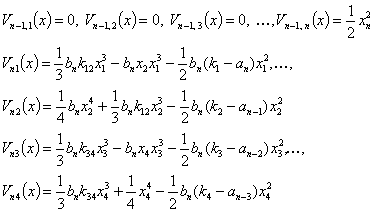
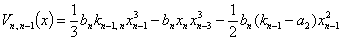
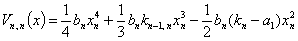
Функцию Ляпунова в скалярной форме можем представить в виде:
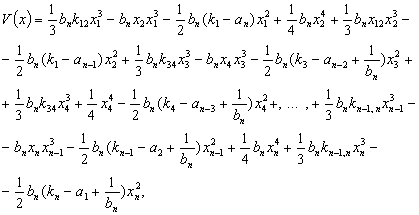(12)
Условия положительной или отрицательной определенности функций (12) неочевидны, поэтому воспользуемся леммой Морса из теории катастроф [6,7].
Рассматриваемая система (3) находится в состоянии устойчивого или неустойчивого равновесия, иначе говоря, является Моросовскими точками [6,7] т. е. система находится в стационарных точках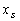 
, где градиент от функций Ляпунова 
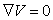и, если
,
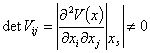то в этих стационарных состояниях системы справедлива лемма Морса и гарантирует существование гладкой замены переменных, такой, что функция Ляпунова (12) локально может быть представлена квадратичной формой:
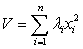(13)
Здесь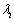 
- собственные значения матрицы Гесса
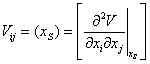
Положительная определенность функций Ляпунова будет определяться знаками коэффициентов квадратичной формы (10), (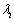>0,i=1, …, n), т. е. знаками собственных значений матрицы Гесса (матрицы устойчивости).
Следовательно, необходимо определить матрицу Гесса в точке равновесия (5). Вычисляем матрицу Гесса для функций Ляпунова (12) в стационарной точке (5). Обозначим:
…
,
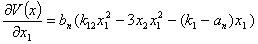
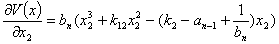
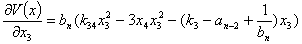
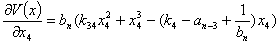
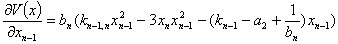
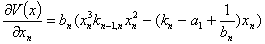Вычисляем элементы матрицы Гесса:
…
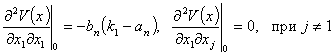
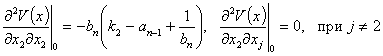
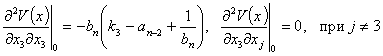
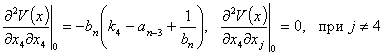
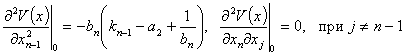
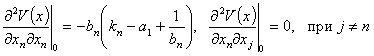
Собственные значения матрицы Гесса:
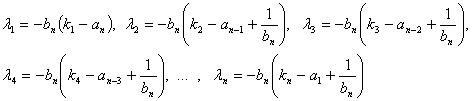
По лемме Морса функцию Ляпунова (12) локально в окрестности стационарного состояния можем представить в виде квадратичной формы:
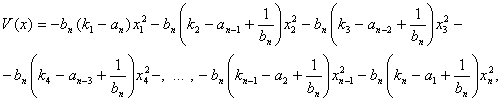(14)
Необходимое условие устойчивости стационарного состояния (5) будет определяться системой неравенств при bn >0:
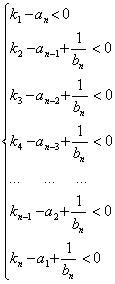(15)
Исследуем робастную устойчивость стационарного состояния (8) на основе метода функций Ляпунова. Уравнение состояния (3) представим в отклонениях относительно стационарного состояния (8).
Формально описанное разложение можно представить в виде:
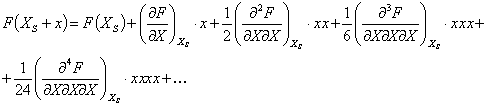
Вычисляем значения производных в стационарной точке (8):
…
…
…
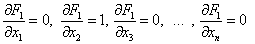
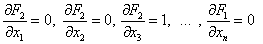
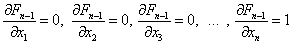
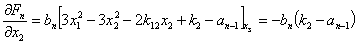
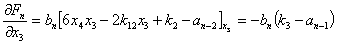
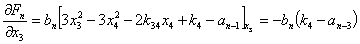
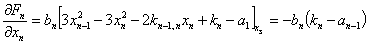
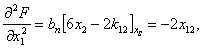
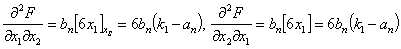
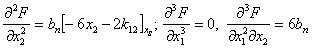
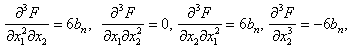
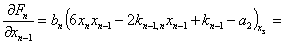
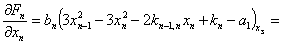
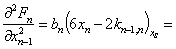
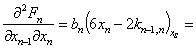
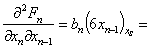
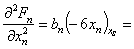
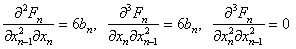
Уравнение состояния (1) в отклонениях относительно стационарного состояния (8) записывается:
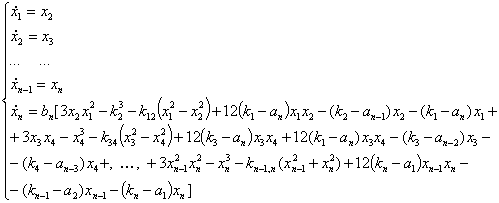
Полная производная по времени от вектор-функций Ляпунова будет определяться:
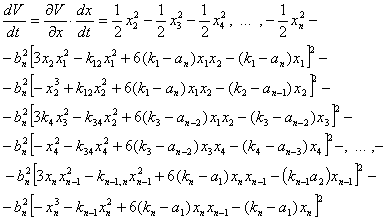(16)
Скалярная функция (16) всегда будет знакоотрицательной, следовательно, достаточное условие асимптотической устойчивости состояния (8) будет всегда выполняться. Обозначим компоненты вектора градиента от вектор-функций Ляпунова:
…
…
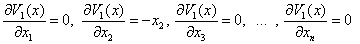
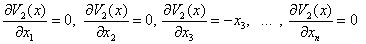
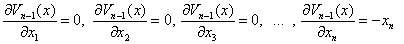
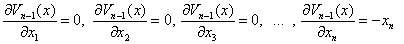
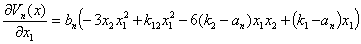
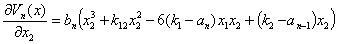
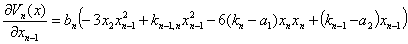
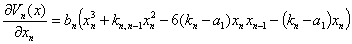
Функцию Ляпунова в скалярной форме представим:
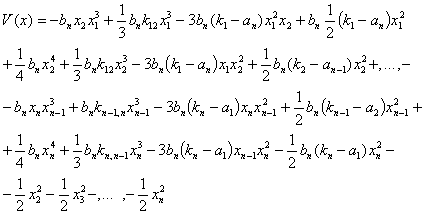(17)
Условия положительной или отрицательной определенности функции (17) определить невозможно, поэтому воспользуемся леммой Морса и локально в окрестности точки стационарного состояния функцию (17) можем представить в виде квадратичной формы:
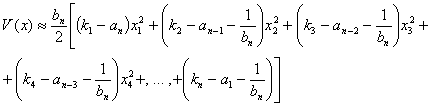(18)
Необходимое условие устойчивости стационарного состояния (8) будет определяться системой неравенств при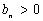 
:
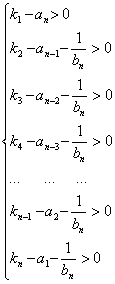(19)
Из системы неравенств (15) и (19) очевидно, что система управления с повышенным потенциалом робастной устойчивости обеспечивает устойчивость системе (3) при любых изменениях неопределенных параметров.
V. Заключение
В работе предлагается универсально новый подход к построению вектор-функций Ляпунова. Компоненты вектора антиградиента вектор-функций из геометрической интерпретации теоремы второго метода Ляпунова задаются компонентами вектора скорости (правой частью уравнения состояния). Исследование робастной устойчивости системы производится путем конструирования некоторой знакоотрицательной функции, равной скалярному произведению вектора градиентов на вектор скорости. Условия устойчивости получаются из положительной определенности вектор-функции Ляпунова, в виде системы неравенств по неопределенным параметрам объектов управления и устанавливаемым параметрам регулятора. Известные методы построения систем управления объектами с неопределенными параметрами в основном посвящены определению робастной устойчивости системы с заданной структурой с линейными законами управления или безынерционными нелинейными (релейными) характеристиками и не позволяют проектировать системы управления с достаточно широкой областью робастной устойчивости в условиях большой неопределенности параметров объекта управления и дрейфа их характеристики в больших пределах.
Фактически результаты, полученные по построению систем управления с повышенным потенциалом робастной устойчивости, позволяют обеспечивать динамическую безопасность и работоспособность управляемых систем на этапе их конструирования и эксплуатации.
Использование разработанного подхода к построению функций Ляпунова позволило наглядно показать, что система имеет асимптотически устойчивые стационарные состояния и в отрицательной, и в положительной области изменения неопределенных параметров объекта управления. При переходе неопределенных параметров через нуль происходит бифуркация и появляются новые устойчивые ветви. При этом нулевое стационарное состояние теряет устойчивость. Эти стационарные состояния одновременно не существуют и появляется возможность синтезировать устойчивую систему при любом изменении неопределенных параметров.
Литература:
1. Поляк Б. Т., Щербаков П. С. Робастная устойчивость и управление. — М.: Наука, 2002. — 303 с.
2. Safonof M. G. Stability and robustness of multivariable feedback systems. — Cambridge, MA: MIT Press, 1980.
3. Chen M. J., Desoer C. A. Necessary and sufficient for robust stability of linear distributed feedback systems // Intern. J. Control. — 1982. — V.35, No.2. — P.255–267.
4. Бесекерский В. А., Небылов А. В. Робастные системы автоматического управления. — М.: Наука, 1983. — 239 с.
5. Gregoire Nicolis, Ilya Prigogine. Exploring Complexity an Introduction. — New York (1989).
6. Постон Г., Стюарт И. Теория катастроф и ее приложения. — М.: Мир, 1980.
7. Гилмор Р. Прикладная теория катастроф. Т.1. — М.: Мир, 1981.
8. Бейсенби М. А. Методы повышения потенциала робастной устойчивости систем управления. — Астана, 2011. — 352 с.
9. Бейсенби М. А. Модели и методы системного анализа и управление детерминированным хаосом в экономике.- Астана, 2011. — 201 с.
10. Бейсенби М. А., Ержанов Б. А. Системы управления с повышенным потенциалом робастной устойчивости. — Астана, 2002. — 164 с.
11. Beisenbi M. А., Nikulin V., Abitova G. А., Ainagulova A. Design of Control System Based on Functions of Catastrophe. // The International Journal of Art & Sciences (IJAS), International Conference for Academic Disciplines, Harvard University, Cambridge, Massachusetts, USA,2012. — Proceedings of the IJAS, 2012. — P. 278–298.
12. Beisenbi M. А., Nikulin V., Abitova G. А. Complex Automation of a Technological Process on the Basis of Control Systems with a Three Level Structure. The 5th Annual IEEE International Systems Conference // The Proceedings of the 2011 IEEE International System Conference (SysCon 2011). -Montreal, Quebec, Canada.- 2011. — P. 34–37.
13. Yermekbayeva J. J., Beisеnbi M., Omarov A, Аbitova G. The Control of Population Tumor Cells via Compensatory Effect. Proceedings of the ICMSCE 2012, Kuala-Lumpur, Malaysia. — 2012. — P. 85–92.
14. Аbitova G., Beisеnbi M., Nikulin V., Ainagulova A. Design of Control Systems for Nonlinear Control Laws with Increased Robust Stability. Proceedings of the CSDM 2012, Paris, France.- 2012. — P.289–310.
15. Барбашин Е. А. Введение в теорию устойчивости — М.: Наука, 1967. — 225 с.
16. Малкин И. Г. Теория устойчивости движения.- М.: Наука, 1966. — 540 с.
17. Воронов А. А., Матросов В. М. Метод векторных функций Ляпунова в теории устойчивости — М.: Наука, 1987. — 312 с.
18. Beisenbi M. A., Kulniyazova K. S., Research of robust stability in control system with Lyapunov direct method, Proceedings of 11-th Inter-University Conference on Mathematics and Mechanics. — Astana, Kazakhstan., 2007.- pp. 50–56.
19. Beisenbi M., Yermekbayeva J. The Research of the Robust Stability in Linear System. // International Conference on Control, Engineering & Information Technology (CEIT’13), Sousse, Tunisia, 2013. — Proceedings of IPCO. — P.142–147.
20. Beisenbi M. А., Abdrakhmanova L. G. Research of dynamic properties of control systems with increased potential of robust stability in a class of two-parameter structurally stable maps by Lyapunov function. // International Conference on Computer, Network and Communication Engineering (ICCNCE 2013). — Published by Atlantis Press, 2013. — P. 201–203.
21. Beisenbi M. A., Yermekbayeva J. J., Beisenbin A. M. The New Control Method of the Research Robust Stability for Linear System. Life Science Journal 2013;10 (12s): — P. 142–148.
