Предложен алгоритм прогнозирующего управления с интегральной составляющей в контуре управления, который позволяет обеспечить астатизм системы и выполнения ограничений, накладываемые на переменные состояния, а также задающие воздействия. Полученный алгоритм реализован для синтеза цифровой системы управления угловой скоростью вращения вала электродвигателя постоянного тока.

Ключевые слова: алгоритм прогнозирования, функционал качества, синтез, ограничения, электропривод, оптимизация.

В работе рассматриваются вопросы синтеза система автоматического управление электромеханическим объектом на основе метода прогнозирующего управления. Метод прогнозирующего управления широко применяется на практике для решения задач синтеза систем автоматического управления, функционирующих в условиях жестких ограничений, накладываемых на переменные состояния и управления [1].

Следует, что метод прогнозирующего управления близок по своей сути к методу локально-оптимального управления [2] и методу оптимального управления с прогнозирующей моделью на основе обобщенного критерия [3].

В работе описывается алгоритм прогнозирующего управления с интегральной составляющей в контуре управления.

Пусть динамика цифровой системы управления описывается уравнениями:

(1)

где  — –мерный вектор состояния, --мерный вектор управления, -- мерный вектор выхода, --мерный вектор возмущений, А, B, C, D — матрицы соответствующих размеров. Области допустимых значений для переменных состояния и управления задаются неравенствами:

где — векторы соответствующих размеров. Необходимо построить управление в виде обратной связи, при котором при , где  — желаемое значение выхода.

В стандартной схеме метода прогнозирующего управления в каждый момент времени решается задача оптимизации квадратичного функционала качества.

(2)

где — симметричная неотрицательно определенная, - симметричные положительно определенные весовые матрицы. Минимум функционала (2) находится с учетом ограничений:

,

где - горизонт управления (натуральное число).

Обозначив через ошибку слежения, получим вектор , удовлетворяющий уравнению:

.

Вектор имеет смысл интеграла от ошибки слежения. Известно [4–6], что решение задачи слежения за заданным значением выхода требует наличия интегральной составляющей в алгоритме управления. Прогнозирующее управление с вектором в контуре управления, строится следующим образом.

Заменив функционал качества (2) на функционал, содержащий интегральную составляющую, получим:

(3)

где - симметричная неотрицательно определенная матрица.

Введем обозначения:

,

,

, , , ,

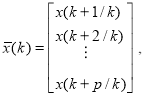
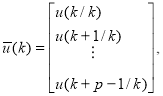
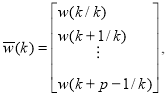
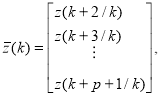
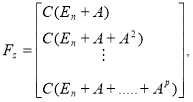
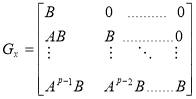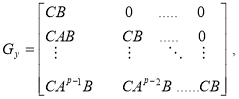
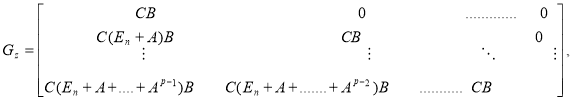
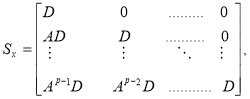
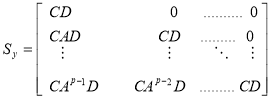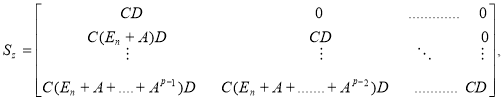
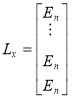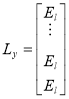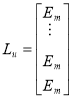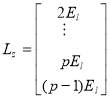где - единичные матрицы размеров и соответственно.

Из уравнений системы (1) следуют соотношения:

Тогда функционал качества (3) принимает вид:

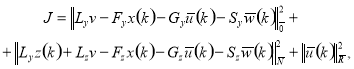(4)

где , и  — блочно-диагональные матрицы с матрицами , и на диагонали. Ограничения на переменные состояния и управления записываются в виде:

. (5)

(6)

Таким образом, имеем задачу квадратично программирования относительно вектора неизвестных с целевой функцией (4) ограничениями (5), (6). С использованием матрицы Гессе целевой функции, которая имеет вид:

.

Очевидно, что положительная гарантирует положительную определенность .

Задача (4)-(6) решается в каждый момент времени . Управление в момент времени полагается равным .

Полученный алгоритм реализован для решения задачи синтеза цифровой системы управления угловой скоростью вращения вала электродвигателя постоянного тока. Пусть динамика электродвигателя описывается уравнениями:

(7)

(8)

где - угловая скорость (рад/с); - сила тока (А); - напряжение (В); - момент внешних сил (Нм); - момент инерции вала двигателя (кг∙м2); - индуктивность якорной цепи (Гн); - сопротивление якорной цепи (Ом); - конструктивные параметры двигателя.

Пусть управление рассчитывается микропроцессором и формируется амплитудно-импульсным модулятором с шагом квантования по времени . Тогда модель дискретной системы принимает вид (1), где:

.

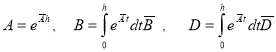Здесь  — матрицы непрерывной системы, представленной в виде (7),(8).

.

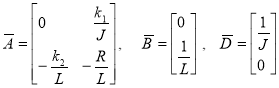Система управления должна обеспечить выполнение условия –заданное значение угловой скорости. Ограничения на переменные состояния и управления заданы неравенствами:

Расчеты проводились в системе MATLAB при следующих значениях параметров объектов управления: , и алгоритма управления: . При решении задачи квадратичного программирования использовалась функция quadprog системы MATLAB.

На рис. 1, 2, 3 показаны переходные процессы по угловой скорости, силе тока и управлению полученные для и . На рис. 4 для сравнения представлены переходные процессы по угловой скорости для системы со стандартным прогнозирующим управлением (линия 1) и для системы с интегральной составляющей в алгоритме управления (линия 2) при . Из результатов моделирования видно, что алгоритм с интегральной составляющей по ошибке слежения обеспечивает астатизм системы в отличие от стандартного алгоритма прогнозирующего управления. Рисунки также наглядно показывают выполнение ограничений по угловой скорости, силе тока и напряжению на входе электродвигателя.

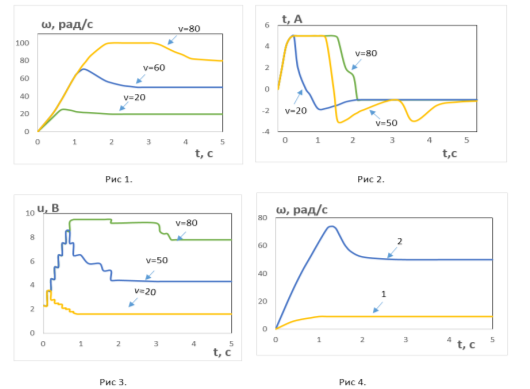
Рис. 1, 2, 3, 4. Графики переходных процессов

Литература:

1.      Clarke D. W. Application of generalized predictive control to industrial processes // IEEE Control Systems Magazine. Vol. 8. 1988 № 2. Р. 49–55.
2.      Смагин В. И., Параев Ю. И. Синтез следящих систем управления по квадратичным критериями Томск: Изд-во ТГУ. 1996. –171с.
3.      Красовский А. А., Буков В. И., Шендрик В. С. Универсальные алгоритмы оптимального управления непрерывными системами. М.: Наука. 1977. –272с.
4.      Пегат А. Нечеткое моделирование и управление. М.: Бином. Лаборатория знаний, 2009. –798с.
5.      Сиддиков И. Х., Измайлова Р. Н. Синтез цифрового алгоритма управления с прогнозирующей моделью // Химическая технология. Контроль и управление. Ташкент. 2010. № 2. –С. 72–76.
6.      Леоненков А. Ю. Нечеткое моделирование в среде Matlab и fuzzyTech. — СПб.: БХВ, 2003. –720с.