Приводится алгоритм параметрической идентификации линейных эргатических систем по экспериментальным данным.
Ключевые слова:эргатические системы, модели, линеаризация, параметрическая идентификация, подготовка операторов.
Известно, в эргатических системах функционирование объекта и оператора настолько тесно связано, что раздельное определение их параметров практически невозможно. С известной долей неопределенности можно свести эргатическую систему к некоторой разомкнутой и определить лишь некоторую обобщенную передаточную функцию. Для этого можно использовать синхронные измерения входных и выходных переменных, полученных в процессе нормальной эксплуатации. Так что параметрическая идентификация возможна лишь с использованием итеративных методов. Такой подход использован для идентификации линеаризованных уравнений продольного движения [1…3]:
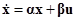, (1)
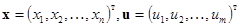— соответственно n-мерный вектор состояния и m-мерный вектор управления, 
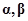— матрицы коэффициентов.
В конечных разностях получим
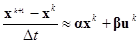
или
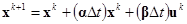
или
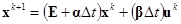
или
,
,
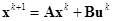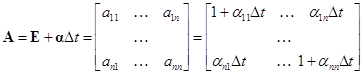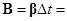
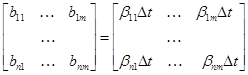, (1')
, 
.
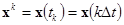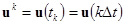Откуда
,
,
…
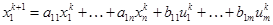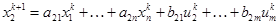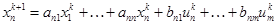. (2)
Введем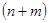 
-мерный вектор
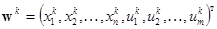(3)
и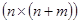 
- матрицу
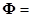
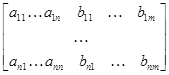. (4)
Из (2)-(4) следует
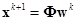. (5)
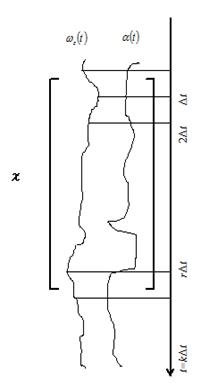
Векторно-матричное уравнение (5) описывает систему с 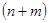входами 
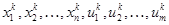и nвыходами 
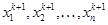(рис.1). Здесь 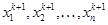определяются изолированно. Поэтому 
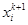, определяемое по i-му уравнению системы (2), является единственной выходной координатой системы с 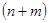входами 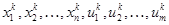(рис.2).
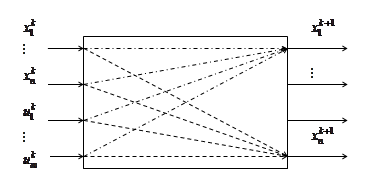
Рис. 1.
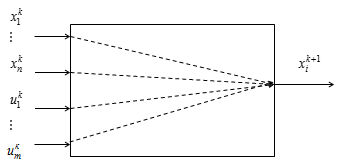
Рис. 2.
Для параметрической идентификации уравнения
, 
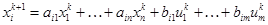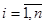
необходимы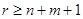 
совокупностей синхронных измерений 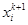и :
,
…
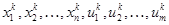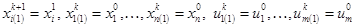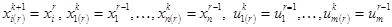(6)
Из предыдущего следует, что приведенные в (6) измерения для каждого i-го выхода 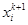удовлетворяют соотношениям:
…
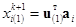
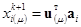
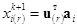, (7)
где
;
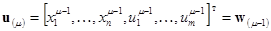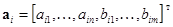. (8)
Из (7) следует
, 
,
.
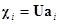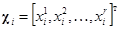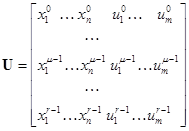Из (2), (7), (8) получим матричное уравнение
.
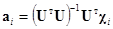Таким образом, оценки элементов матриц 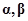определятся по соотношениям (1') и
.
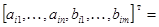
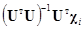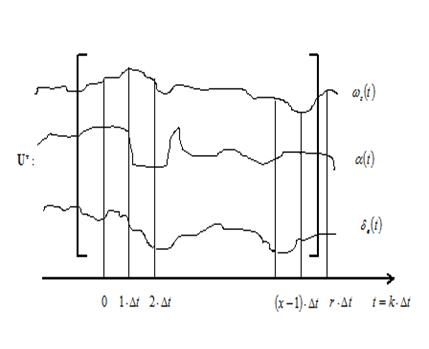
Пример составления матриц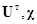 
для продольного движения приводится рис.3 (используются стандартные обозначения для углов тангажа 
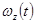, атаки 
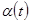и отклонения руля 
).
|
|
|
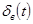Рис. 3. Схема определения матриц 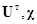по синхронным измерениям фазовых координат
Литература:
1. Авиационные тренажеры модульной архитектуры: монография; под редакцией Лапшина Э. В., д.т.н., проф. Данилова А. М. — Пенза, ИИЦ ПГУ. — 2005. — 146 с.
2. E. Budylina, A. Danilov, I. Garkina. Control of multiobjective complex systems / Contemporary Engineering Sciences, Vol. 8, 2015, no. 10, 441–445. http://dx.doi.org/10.12988/ces.2015.5276.
3. Будылина Е. А., Гарькина И. А., Данилов А. М. Приближенные методы декомпозиции при настройке имитаторов динамических систем / Региональная архитектура и строительство. — 2013. — № 3. — С. 150–156.
