Рассматриваются практические вопросы определения градуировочных характеристик средств измерений, используемых для анализа кинетики формирования физико-механических характеристик композиционных материалов при их аппроксимации ортогональными полиномами Чебышева.
Ключевые слова: композиты, свойства, средства измерений, градуировочные характеристики, аппроксимация, точность.
После определения математической модели системы проводится ее параметрическая идентификация (определение числовых параметров математической модели, при которых решение задачи соответствовало бы экспериментальным данным; найденные значения констант не должны противоречить физическому смыслу и теоретическим соображениям). Результаты во многом будут определяться точностью используемых средств измерений. Модели могут быть в разной степени формализованными [1…4], но все они должны обладать главным свойством: связать результаты наблюдений в некоторую общую картину. Численные характеристики изучаемой системы (процесса) могут быть константами (не изменяются в ходе процесса) или переменными. Часть из них может быть измерена лабораторными методами в ходе эксперимента (измеряемые константы и переменные), а другая либо вообще не может быть измерена современными методами, либо их измерение чрезвычайно трудоемко и дорого (не измеряемые константы и переменные).
Выбор метода идентификации определяется неоднозначно, ибо в самой постановке задачи заранее предполагается неопределенность (неполнота знаний об объекте, ограничения в наблюдениях объекта во времени, неточность измерения сигналов на входе и на выходе объекта и т. п.).
В силу значительной сложности структурная идентификация часто сводится к эвристическому заданию структуры модели, опираясь на априорные данные. Здесь эффективность последующей параметрической идентификации во многом определяется тем, насколько удачно была выбрана структура модели. В известных методах параметрической идентификации учитываются особенности исследуемой системы, условия функционирования, способ тестирования, способы анализа экспериментальных данных, вид получаемых моделей и др.
Всегда важным остается выбор процедуры сравнения для оценки адекватности получаемой модели объекту. Основное требование к модели — адекватность объекту изучения; иначе теряется смысл моделирования. Создание адекватной модели возможно лишь в случае, когда свойства и взаимосвязи моделируемого объекта в достаточной степени изучены. Адекватность частных математических моделей для описания формирования физико-механических характеристик материалов в значительной степени определяется выбором и поверкой средств измерений (по точности градуировочных характеристик [5,6]).
Рассмотрим использование ортогональных полиномов Чебышева 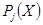 для аппроксимации градуировочных характеристик с указанием и способа выбора степени аппроксимирующего полинома.
для аппроксимации градуировочных характеристик с указанием и способа выбора степени аппроксимирующего полинома.
Предполагается, что экспериментальные значения 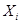 известны точно; значения
известны точно; значения 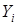 содержат погрешности, которые имеют приближенно гауссовское распределение с дисперсиями
содержат погрешности, которые имеют приближенно гауссовское распределение с дисперсиями 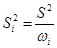 . Тогда по данным
. Тогда по данным 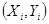 можно последовательно построить, используя МНК, приближения полиномами со степенями
можно последовательно построить, используя МНК, приближения полиномами со степенями 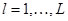 :
:
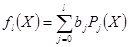 ,
, 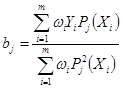 .
.
Максимальную степень полинома обычно выбирается, исходя из конкретной задачи (в большинстве случаев 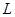 не превышает 5).
не превышает 5).
Далее вычисляются остаточные суммы квадратов
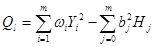
и оценки дисперсии 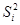 , соответствующие различным степеням
, соответствующие различным степеням 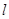 :
:
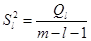 .
.
Степень полинома повышают до тех пор, пока оценки 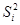 заметно убывают. Выбор степени полинома
заметно убывают. Выбор степени полинома 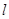 осуществляется, исходя из точности построения ГХ в конкретной методике. При поверке используемых средств измерений характеристик композитов значение
осуществляется, исходя из точности построения ГХ в конкретной методике. При поверке используемых средств измерений характеристик композитов значение 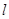 выбиралось из условия, чтобы оценка
выбиралось из условия, чтобы оценка 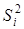 была минимальна (
была минимальна (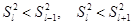 ); а также при принятом значении
); а также при принятом значении 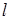 оценка
оценка 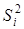 перестает заметно убывать (
перестает заметно убывать (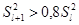 ). Если при всех степенях
). Если при всех степенях 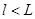 выбранное условие не достигается, то максимальная степень полинома принимается равной
выбранное условие не достигается, то максимальная степень полинома принимается равной 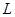 .
.
Для выбора степени полинома можно использовать и методы перекрестного выбора. Здесь все данные разбивают на 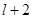 группы (конкретные способы разбиения могут быть различны и устанавливаются в методиках). Одна из групп является проверочной, а по медианным точкам остальных групп строится полином
группы (конкретные способы разбиения могут быть различны и устанавливаются в методиках). Одна из групп является проверочной, а по медианным точкам остальных групп строится полином 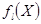 . Согласие полинома с исходными данными оценивается по его отклонению от медианы проверочной выборки:
. Согласие полинома с исходными данными оценивается по его отклонению от медианы проверочной выборки:
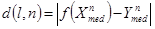 .
.
Описанную процедуру повторяют многократно, принимая последовательно каждую из групп за проверочную. В результате получится суммарный показатель адекватности полинома 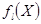 исходным данным:
исходным данным:
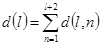 .
.
В качестве искомой степени полинома принимается значение 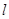 , для которого показатель
, для которого показатель 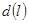 минимален.
минимален.
Рассмотрим далее оценку погрешностей ГХ, представленных в аналитической форме 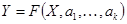 , которая производится на основе линеаризованного разложения
, которая производится на основе линеаризованного разложения
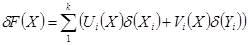 ,
,
где коэффициенты
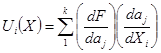 ,
,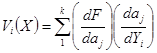 ,
,
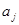 - оценки параметров ГХ по данным
- оценки параметров ГХ по данным 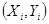 ,
, 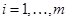 ; все производные вычисляются в точке
; все производные вычисляются в точке 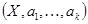 .
.
Если границы погрешностей измерений величин 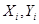 есть
есть 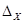 и
и 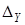 , то границы погрешности ГХ в точке
, то границы погрешности ГХ в точке 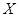 определятся из:
определятся из:
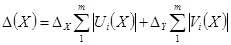 .
.
При известных характеристиках случайных и систематических составляющих погрешностей измерений величин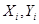 характеристики погрешности ГХ в точке
характеристики погрешности ГХ в точке 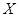 определятся из условий:
определятся из условий:
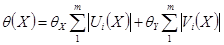 ,
,
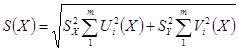 .
.
При этом доверительные границы случайной погрешности ГХ в точке 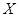 оценивают по формуле
оценивают по формуле
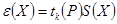 ,
,
где 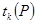 - коэффициент Стьюдента при вероятности
- коэффициент Стьюдента при вероятности 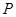 с числом степеней свободы
с числом степеней свободы 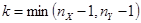 ,
, 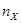 и
и 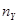 — объемы выборок, по которым получены оценки
— объемы выборок, по которым получены оценки 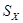 и
и 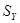 .
.
Если известно, что погрешности исходных данных изменяются нерегулярным образом в заданных границах 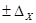 ,
, 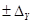 , то можно построить приближенные доверительные границы погрешности ГХ в точке
, то можно построить приближенные доверительные границы погрешности ГХ в точке 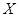
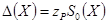 ,
,
исходя из 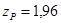 при
при 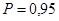 ;
; 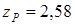 при
при 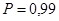
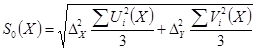 .
.
Если систематические погрешности исходных данных изменяются нерегулярным образом в заданных границах 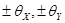 , то приближенные границы систематической погрешности ГХ в точке
, то приближенные границы систематической погрешности ГХ в точке 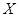 вычисляются по формулам
вычисляются по формулам
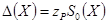 ,
, 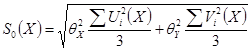 .
.
Если систематические погрешности исходных данных остаются примерно постоянными для всех точек диапазоне, то границы систематической погрешности ГХ в точке 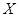 оценивают по формуле
оценивают по формуле
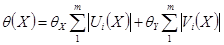 .
.
Предложенная методика использовалась при построении математических моделей отдельных свойств композиционных материалов [2,3,4,7].
Литература:
1. Сложные системы: идентификация, синтез, управление: монография / Данилов А. М., Гарькина И. А. — Пенза: ПГУАС. — 2011. — 308 с.
2. Гарькина И. А., Данилов А. М., Королев Е. В. Математическое и компьютерное моделирование при синтезе строительных композитов: состояние и перспективы / Региональная архитектура и строительство. — 2010. — № 2. — С. 9–13.
3. Данилов А. М., Гарькина И. А. Математическое моделирование сложных систем: состояние, перспективы, пример реализации. / Вестник гражданских инженеров. –2012. — № 2. — С. 333–337.
4. Королев Е. В., Смирнов В. А., Прошин А. П., Данилов А. М. Моделирование эволюции лиофобных дисперсных систем / Известия высших учебных заведений. Строительство. — 2004. — № 8. — С. 40–46.
5. Планирование эксперимента. Обработка опытных данных: монография / И. А. Гарькина [и др.]; под ред. проф. А. М. Данилова. — М.: Палеотип. — 2005. — 272 с.
6. Хнаев О. А., Данилов А. М. Методы планирования эксперимента в аппроксимации функций многих переменных / Молодой ученый. — 2014. — № 4. — С. 295–297.
7. Гарькина И. А., Данилов А. М. Опыт разработки композиционных материалов: некоторые аспекты математического моделирования / Известия ВУЗов. Строительство. — 2013. — № 8 (656). — С.28–33.

