Определяются инженерно-психологические аспекты, непосредственно связанные с оценкой качества имитационного моделирования объектов управления, описываемых системой обыкновенных дифференциальных уравнений в нормальной форме Коши.
Ключевые слова: транспортные системы, подготовка операторов, качество подготовки операторов, имитационное моделирование объекта управления, критерии качества.
Основное требование к обучающим комплексам для подготовки операторов эргатических транспортных систем состоит в обеспечении формирования стиля и навыков управления оператора реальным объектом в условиях, когда объект заменяется на имитационную модель [1…3]. Для многоцелевых систем практически отсутствует возможность точного описания объекта его моделью, особенно при противоречивых критериях. Нельзя добиться стопроцентной адекватности модели и реального объекта. Поэтому всегда можно говорить лишь о некоторой заданной степени адекватности, достаточной для решения некоторых основных видов деятельности оператора. Так, навыки управления органами управления летательным аппаратом могут быть сформированы с помощью имитационной модели, весьма далекой от требуемой адекватности. Например, при формировании вполне конкретного стиля управления реальным летательным аппаратом с конкретными динамическими характеристиками первичные навыки обращения с органами управления летательным аппаратом в известной степени такие же, как и при управлении другими техническими объектами. Отсюда следует первый важный вывод: характеристики имитационной модели должны выбираться, исходя из конкретных задач, которые должны решаться на обучающем комплексе.
Непосредственно из этого вытекает необходимость решения другой задачи: как описать навыки и стиль управления, что под этим понимать и как осуществить формализацию этих понятий? Ясно, что решение этой задачи невозможно без формулировки и описания понятия «управляющее воздействие оператора». В настоящее время обучающие комплексы для транспортных систем представляют собой сложные технические устройства, использующие математическую модель объекта управления (полученную исходя из заданной степени точности). Обычно на временном интервале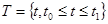 
хорошим приближением является модель, описываемая обыкновенными дифференциальными уравнениями в нормальной форме Коши. В векторной форме модель представляется в виде:
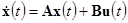; (1)
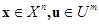— соответственно векторы состояния и управления; 
; 
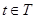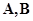- матрицы, определяемые техническими параметрами объекта. В (1) предполагается непрерывность по совокупности переменных 
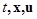и непрерывная дифференцируемость по 
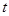и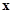 
. Поведение вектора 
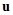может быть произвольным; уравнение (1) определяет управляемый процесс. Ход управляемого процесса определяется на некотором интервале 
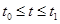, если на этом интервале вектор 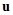задан в виде
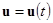; (2)
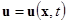. (3)
Вектор-функция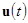 
является программным управлением, а 
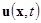— законом управления. Как видим, каждому выбору вектора управления 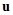и каждому начальному состоянию 
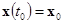при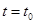 
по (1) соответствует временная последовательность состояний 
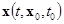, которой определяется программное движение системы 
.
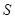Система управлений в соответствии с (1) при заданных начальных условиях имеет вид
,
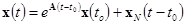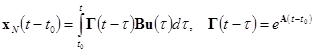. (4)
Таким образом, движение объекта описывается уравнением (1) в некоторой области изменения параметров, определяемой эксплуатационным диапазоном его применения. Решение (4) характеризует опорные траектории, соответствующие заданным начальным условиям при выбранном векторе управлении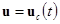 
. Оценка точности воспроизведения характеристик объекта в обучающем комплексе может производиться по соотношению:
;
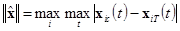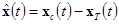, (5)
где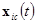 
— характеристики реального объекта, полученные при его натурных испытаниях по регламентированным методам; 
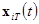— расчетные характеристики объекта при тех же начальных условиях, что и в (1).
Для объекта с системой автоматического управления 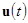представляется в виде
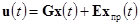, (6)
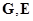-соответственно матрицы управления по обратной связи и по вектору программных сигналов 
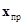. Решения (1) и (6) для момента времени 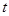имеют вид:
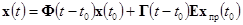, (7)
,
.
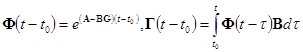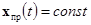Выражением (7) описываются характеристики контура «объект — САУ».
Как правило, разработка имитационных моделей осуществляется при ограниченных сведениях и неполной информации о динамических свойствах имитируемого объекта. Поэтому нередко точность математической модели (1) по критерию (5) оказывается недостаточной. Необходимы структурная и параметрическая идентификации объекта (основная техническая проблема синтеза обучающих комплексов, определяющая эффективность и качество подготовки операторов).
Обучающий комплекс в настоящее время строится по модульному принципу, каждый из которых является моделью отдельных подсистем. Однако надо помнить, что соединение даже совершенных имитаторов в единую иерархическую структуру может привести к получению суммарных погрешностей моделирования, искажающих воспринимаемую оператором приборную, визуальную, акселерационную и др. информацию. Пришли ко второй основной технической проблеме синтеза обучающих комплексов. Указанные две проблемы являются определяющими при формировании навыка управления на обучающем комплексе. Задача сводится к сравнению двух эргатических систем: «оператор — модель объекта», «оператор — реальный объект». Модель каждой из указанных эргатических систем будет вместо уравнения (1) описываться уравнением вида:
,
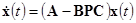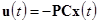, (8)
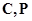— соответственно матрицы параметров информационной модели и оператора.
Если уравнения (1), (3) описывают движения объекта (модели) в контуре управления с САУ, то (9) характеризует эргатическую систему «оператор — объект» («оператор — информационная модель») в режиме ручного управления. Матрицей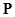 
учитываются особенности восприятия и переработки оператором поступающей информации и формирования нам этой основе управляющих движений. Однако невозможно предопределить реакцию оператора на информацию, получаемую в искусственных условиях, когда при обучении используется модель объекта. Это и является основным психофизиологическим аспектом проблемы синтеза обучающих комплексов, влияющим на формирование навыков управления.
Указанные выше аспекты являются методологической основой проектирования обучающих комплексов, которые неоднократно использовались при разработке тренажеров различного назначения [4…6].
Литература:
1. E. Budylina, A. Danilov, I. Garkina. Control of multiobjective complex systems / Contemporary Engineering Sciences, Vol. 8, 2015, no. 10, 441–445. http://dx.doi.org/10.12988/ces.2015.5276.
2. Данилов А. М., Гарькина И. А., Дулатов Р. Л. Ретроспективная идентификация сложных систем // Региональная архитектура и строительство. — 2015. — № 1(22) –С.130 -136.
3. Будылина Е. А., Гарькина И. А., Данилов А. М., Дулатов Р. Л. Структурная и параметрическая идентификация сложных эргатических систем / Фундаментальные исследования. –№ 2. -2015. — С.919–922.
4. Будылина Е. А., Гарькина И. А., Данилов А. М., Тюкалов Д. Е. Параметрическая идентификация эргатической системы с помехами /Современные проблемы науки и образования. — 2015. — № 1; URL:http://www.science-education.ru/121–17681
5. E. Budylina, A. Danilov. Approximation of aerodynamic coefficients in the flight dynamics simulator / Contemporary Engineering Sciences, Vol. 8, 2015, no. 10, 415–420. http://dx.doi.org/10.12988/ces.2015.5256.
6. A.Danilov, I.Garkina. Coherence function in analysis and synthesis of complex systems / Contemporary Engineering Sciences, Vol. 8, 2015, no. 9, 375–380. http://dx.doi.org/10.12988/ces.2015.5236.
