Разработан алгоритм интервального оценивания параметров нелинейных моделей методом наименьших квадратов без вычисления производных. Рассмотрены статистические аспекты алгоритма и дано описание соответствующей программы для ПЭВМ. Приводятся примеры решения конкретных задач из области физической химии.
Ключевые слова: математическое моделирование, прикладное нелинейное программирование, задачи оптимизации, нелинейное оценивание параметров, метод наименьших квадратов, доверительная область
Задача интервального оценивания параметров математической модели путём статистической обработки опытных данных по методу наименьших квадратов (МНК) состоит из двух этапов. 1) нахождение вектора оценок параметров, минимизирующих сумму квадратов отклонений, 2) определение доверительной области для найденного вектора.
В случае линейной модели оба этапа решаются матричными операциями [1]. Мерами неопределённости и взаимосвязи оценок параметров служат элементы обратной матрицы системы нормальных уравнений; оценкой точности параметра − его стандартное отклонение, которое вычисляется из соответствующего диагонального элемента обратной матрицы и дисперсии погрешностей регрессии. Интервальными оценками являются индивидуальные или совместные доверительные интервалы, соответствующие заданной доверительной вероятности. То же относится к линеаризованной модели (например, в МНК по Гауссу-Зайделю [2, стр. 404–415]), но применительно к исходной нелинейной модели такое интервальное оценивание является приближённым [там же, стр. 429–440]. Минимизация суммы квадратов методами без производных («прямым поиском») не дает информации о доверительной области, но, как показано в [3], при особом задании целевой функции задача интервального оценивания может быть решена и в этом случае. В рамках данного подхода разработан алгоритм и создана программа «GLSM» (Generalized Least Squares Method), рассмотрение которых является целью данной работы.
I. Постановка и решение задачи
-
Найти точечные оценки
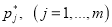 , вектора параметров
, вектора параметров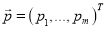 модели
модели 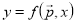 на основании наблюдений
на основании наблюдений 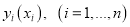 , путем минимизации суммы квадратов отклонений
, путем минимизации суммы квадратов отклонений
![]() .(1)
.(1)
-
В соответствии с [3] в качестве меры неопределённости оценок
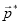 взять протяжённость совместной доверительной области
взять протяжённость совместной доверительной области
![]() (2)
(2)
вдоль координатных направлений ![]() пространства параметров. В формуле (2):
пространства параметров. В формуле (2): ![]() − оценка дисперсии погрешностей наблюдений,
− оценка дисперсии погрешностей наблюдений, ![]() − квантиль распределения Фишера для числа степеней свободы m, n — m и уровне значимости
− квантиль распределения Фишера для числа степеней свободы m, n — m и уровне значимости ![]() .
.
Требуется найти экстремальные (т. е. наиболее удалённые от ![]() ) значения каждого из компонентов pj вектора
) значения каждого из компонентов pj вектора ![]() , принадлежащего границе доверительной области
, принадлежащего границе доверительной области
![]() .(3)
.(3)
Важно отметить два обстоятельства.
-
В частном случае, когда
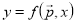 линейна, доверительная область есть эллипсоид. Если в правой части (3) присутствует только
линейна, доверительная область есть эллипсоид. Если в правой части (3) присутствует только 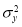 , тогда экстремальные значения компонентов
, тогда экстремальные значения компонентов 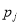 соответствуют границам интервалов
соответствуют границам интервалов 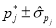 , где
, где 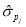 — оценка стандартного отклонения (среднеквадратичная ошибка) параметра.
— оценка стандартного отклонения (среднеквадратичная ошибка) параметра.
- Чем более нелинейна модель и больше доверительная вероятность (меньше уровень значимости α, больше квантиль Fα), тем удаленнее граница (3) от минимума, и тем больше доверительная область отличается от эллипсоида. Поэтому экстремальные отклонения в общем случае не симметричны относительно точки минимума, но характеризуют протяжённость совместной доверительной области точно (в отличие от методов линеаризации). Неопределенность связана лишь с величиной доверительной вероятности 1- α.
Пусть ![]() и
и ![]() − расстояния от точки минимума
− расстояния от точки минимума ![]() до плоскости, касательной к границе совместной доверительной области (3) и перпендикулярной j-ой координатной оси. Тогда значения
до плоскости, касательной к границе совместной доверительной области (3) и перпендикулярной j-ой координатной оси. Тогда значения ![]() на границе равны (рис. 1)
на границе равны (рис. 1)
![]() .(4)
.(4)
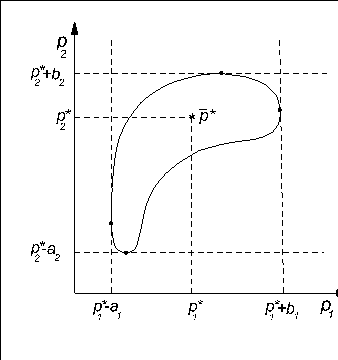
Рис. 1. Совместная доверительная область для нелинейной модели в произвольном двумерном изображении и экстремальные значения параметров на границе
Задача этапа сводится к отысканию значений компонентов (4) вектора параметров, которые удовлетворяют условию (3):
найти ![]() ;
; ![]() ,
,
т. е. к минимизации величин ![]() и
и ![]() (
(![]() ) при ограничении, заданном в виде равенства.
) при ограничении, заданном в виде равенства.
Преимуществом такой постановки является то, что в одной программе можно применить в виде процедуры единый алгоритм минимизации для двух целей: отыскания точечных МНК-оценок параметров, а затем их экстремальных отклонений. Алгоритм минимизации в принципе может быть любым подходящим, но отдано предпочтение методу, не использующему производных — алгоритму деформируемого многогранника (модифицированный симплекс-метод) по Нелдеру и Миду [4, стр. 163]. Преимущества способов минимизации без производных состоят в их относительной простоте и устойчивости к выбору начального приближения. Отпадает необходимость в аналитических выкладках и программировании процедуры для производных.
Реализуется следующий вариант метода штрафных функций, при котором минимизация с ограничениями сводится к последовательности процедур минимизаций без ограничений. В качестве целевой функции (ЦФ) выбирается переменная![]() при поиске
при поиске![]() и
и ![]() при поиске
при поиске ![]() , а мерой отклонения от условия (3) служит штраф
, а мерой отклонения от условия (3) служит штраф
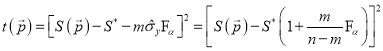 , возводящий квадратичный барьер возле границы гиперповерхности совместной доверительной области.
, возводящий квадратичный барьер возле границы гиперповерхности совместной доверительной области.
Для каждого j = 1,…, m последовательно ищутся минимальные значения штрафных функций
![]() , (k — номер приближения),
, (k — номер приближения),
где величина ωk (вес штрафа), изменяется так, чтобы по мере приближения ![]() к границе доверительной области требования к выполнению условия (3) возрастали. Если при достижении ω = ωmax граница еще не найдена, считается, что для данного параметра граница отсутствует (параметр
к границе доверительной области требования к выполнению условия (3) возрастали. Если при достижении ω = ωmax граница еще не найдена, считается, что для данного параметра граница отсутствует (параметр ![]() незначим). Стратегия изменения ωk является одной из ключевых проблем в методе штрафных функций. Часто исследователю приходится выбирать ее исходя из свойств каждой конкретной задачи. В рассматриваемом случае наиболее универсальной и эффективной оказалась стратегия: ωk = 0, если выполнено (2), иначе ωk+1 = 4ωk; ω1 = 10.
незначим). Стратегия изменения ωk является одной из ключевых проблем в методе штрафных функций. Часто исследователю приходится выбирать ее исходя из свойств каждой конкретной задачи. В рассматриваемом случае наиболее универсальной и эффективной оказалась стратегия: ωk = 0, если выполнено (2), иначе ωk+1 = 4ωk; ω1 = 10.
II. Масштабирование задачи.
Проблемы и приемы масштабирования переменных и параметров в задачах оптимизации детально рассмотрены в [2, стр. 422–428]. Для методов без производных важно, чтобы компоненты вектора ![]() имели величину порядка 1 (начальный шаг симплекса). С этой целью для
имели величину порядка 1 (начальный шаг симплекса). С этой целью для ![]() вводится вектор масштабных множителей
вводится вектор масштабных множителей ![]() . Его конкретное значение находится по правилу: после минимизации S принять
. Его конкретное значение находится по правилу: после минимизации S принять ![]() и поиск S* повторить. В итоге будет получено:
и поиск S* повторить. В итоге будет получено: ![]() , модель
, модель ![]() станет нормированной. Масштаб для
станет нормированной. Масштаб для ![]() выбирается так, чтобы штраф в точке
выбирается так, чтобы штраф в точке ![]() также был равен 1, т. е. масштабный множитель штрафа μT находится из условия
также был равен 1, т. е. масштабный множитель штрафа μT находится из условия
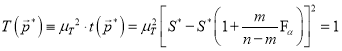 .
.
Отсюда
![]() .(5)
.(5)
Вводятся нормированные суммы квадратов:
![]() .
.
С учетом (5)
![]() .
.
Выражение для масштабированного штрафа принимает вид:
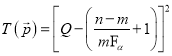 .
.
III. Описание программы
Алгоритм реализован в виде макроса в среде VBA Excel пакета MS Office для ОС Windows версии XP и выше.
1. Идентификаторы программы:
m — число параметров функции-модели; n — число точек регрессии;
step0, step — начальный и рабочий шаг исходного многогранника (симплекса);
alfa, beta, gamma — соответственно, коэффициенты отражения, сжатия и растяжения деформируемого многогранника (ДМ);
eps1 — минимальный объём ДМ; eps2 — точность определения границ;
Fi — квантиль распределения Фишера; Ms — масштабный множитель μT;
W — вес штрафа; Wmax — предельный вес штрафа; Disp — оценка дисперсии, ![]() ;
;
Ulog, Vlog, V — целые числа, определяющие поток алгоритма;
i, j — зарезервированные индексы массивов вершин ДМ, значений целевой (ЦФ) или штрафной (ШФ) функции и массива вектора параметров; u — зарезервированный индекс массивов регрессии;
Rn — индекс параметра, для которого ищется экстремальное отклонение;
F1 — значение функции-модели (ФМ); F2 — значение ЦФ или ШФ;
S2 — нормированная сумма квадратов; Penalty — нормированный штраф; I1 — счетчик;
alarm — Булевская переменная, принимающая значение True в случае, когда количество вычислений ЦФ в одном цикле (I1) превысит заданное число или ШФ достигнет определенного (неприемлемого) предела.
2. Массивы:
X(1 to n), Y(1 to n) — массивы абсцисс и ординат точек регрессии;
P(1 to m), PL(1 to m), Mp(1 to m) — массивы векторов ![]() ,
, ![]() и
и ![]() ;
;
F(1 to m + 4) — массив значений ЦФ или ШФ в вершинах ДМ;
S(1 to m + 4) — массив координат ДМ.
3. Процедуры:
Sub MF(u) — вычисление ФМ; Sub OF() — вычисление ЦФ или ШФ;
Sub RT() — вывод регрессионной таблицы (РТ);
Sub CT() — очистка таблиц от результатов предыдущих вычислений([1]):
Sun Norm() — нормировка модели;
Sub Rec() — приведение модели к исходному виду;
Sub Simplex() — минимизация по Нелдеру и Миду;
Sub GLSM() — собственно программа «GLSM».
Алгоритм Sub Simplex() является основой самостоятельной программы «Simplex» в Excel VBA; он был рассмотрен ранее [5] и входит в «GLSM» как общая процедура минимизации.
IV. Блок-схема алгоритма «GLSM» представлена на рис. 2.
V. Порядок работы с программой
Программа «GLSM» опубликована в сети Интернет. Чтобы пользоваться ею, на ПК с операционной системой MS Windows XP или более поздней([2]), должно быть установлено приложение MS Office Excel.
Проделать следующее:
- Загрузить и сохранить файл программы glsm.xls, пройдя по ссылке [6].
- Открыть приложение Excel, не открывая файла.
- Программа является макросом, поэтому необходимо снизить уровень безопасности приложения, для чего войти в основном меню по пути: Сервис > Макрос > Безопасность; на открывшейся вкладке выбрать средний уровень безопасности.
Открыть файл программы и в открывшемся окне предупреждения системы безопасности выбрать «Не отключать макросы». Появится главное окно программы — «GLSM». Кроме того, имеются ещё две вкладки: «Константы» и «Регрессия». Из констант следует ввести во второй столбец: число параметров функции-модели, m, число точек регрессии, n, квантиль критерия Фишера, Fi = Fα(m,n-m)([3]). Кроме того, необходимо ввести целочисленные значения для констант Ulog и Vlog. При Ulog = 1 осуществляется (а) точечное оценивание ![]() и (б) заполняется регрессионная таблица, а при нулевом значении пропускается пункт а. Константа Vlog задает вариант поиска границ: -1 — левая, 1 — правая, 2 — обе, 0 — ни одна. Прочие константы установлены по умолчанию и их можно не менять. На вкладке «Регрессия» размещается регрессионная таблица, где надо заполнить столбцы X(u) и Y(u) согласно заданной величине n.
и (б) заполняется регрессионная таблица, а при нулевом значении пропускается пункт а. Константа Vlog задает вариант поиска границ: -1 — левая, 1 — правая, 2 — обе, 0 — ни одна. Прочие константы установлены по умолчанию и их можно не менять. На вкладке «Регрессия» размещается регрессионная таблица, где надо заполнить столбцы X(u) и Y(u) согласно заданной величине n.
Для просмотра программного кода и занесения необходимых описаний конкретных функций надо пройти из основного меню по пути: Сервис > Макрос > Редактор Visual Basic. Откроется окно Microsoft Visual Basic — glsm.xls([4]). Тексты процедур отображены на листах-модулях. Module2 содержит Sub Simlplex(), а Module1 — Sub GLSM() и остальные процедуры.
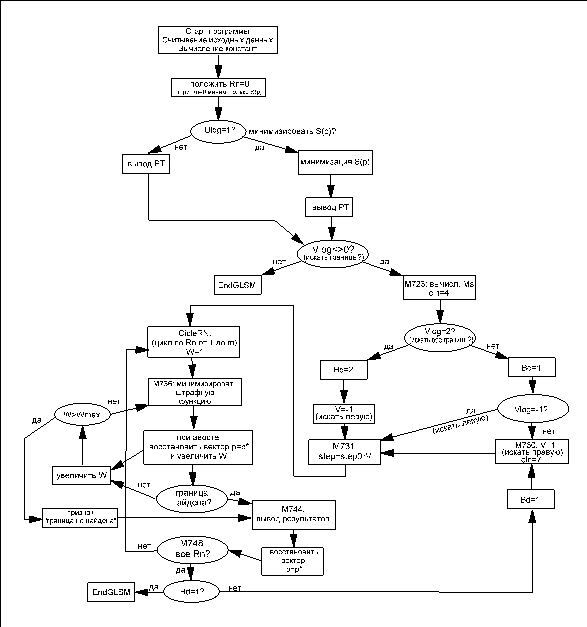
Рис. 2. Блок-схема алгоритма «GLSM»
Дальнейший порядок работы с программой лучше рассмотреть на конкретных примерах.
10. Оценивание констант скоростей химической реакции.
Требуется найти интервальные МНК-оценки параметров двухстадийной химической реакции типа A → B → C. Функция-модель для описания зависимости концентрации y промежуточного продукта от времени x имеет вид([5]):
![]() .(6)
.(6)
Исходные данные для расчёта следующие (табл.1):
Таблица 1
Исходные данные для функции-модели (6).
|
u |
xu |
yu |
|
1 |
0.5 |
0.263 |
|
2 |
1.0 |
0.455 |
|
3 |
1.5 |
0.548 |
Решение задачи. Записать процедуру Sub MF(u)([6]), приняв, что p1→P(1); p2→P(2); xu →X(u); yu →Y(u); y →F1:
Sub MF(u) 'функция-модель для задачи 3.44 Химмельблау
Dim X1 As Single, P1, P2 As Double ' вспомогательные
X1 = X(u) ' аргумент
P1 = Mp(1)*P(1): P2 = Mp(2)*P(2) ' масштабированные параметры ФМ
F1 = P1 * (Exp(-P2 * X1) — Exp(-P1 * X1)) / (P1 — P2)
End Sub
На вкладке «Константы» ввести: m → 2; n → 3, Ulog = 1, Vlog = 0 (на 1-м этапе, пока модель не нормирована, границ не искать). Для получения среднеквадратичных ошибок параметров положить Fi = 1/m = 0.5. Очистить таблицы от результатов предыдущих вычислений можно, нажав <ctrl+t>. Начальные оценки ввести на вкладке «GLSM»; например, (1; 0.5)T (в данном примере недопустимы одинаковые значения начальных параметров). Надо иметь в виду, что в дробных числах в таблицах используется запятая, а в программном коде — десятичная точка. Данные табл. 1 внести в соответствующие столбцы на вкладке «Регрессия». Запустить «GLSM» нажатием <ctrl+g>. Результат 1-го этапа (округлено до 3-х знаков): ![]() ; (I1 = 69).
</ctrl+g></ctrl+t>
; (I1 = 69).
</ctrl+g></ctrl+t>
На 2-м этапе нормируем модель, нажав <ctrl+n>. Уточняем расчёт (<ctrl+g>) и получим: ![]() ; (I1 = 54). Модель можно считать нормированной. На 3-м этапе ищем границы, положив на вкладке «Константы» Vlog→2. Расчет (<ctrl+g>) даст результат для нормированной модели. После пересчета на исходную модель (<ctrl+i>) получим оценки «стандартных отклонений»: a1 = 0.0403; b1 = 0.0400; a2 = 0.0587; b2 = 0.0551. Поиск границ с точностью eps2 = 10–4 достигнут при W = 10; число обращений (I1) к процедуре вычисления ШФ от 96 до 119. Тот факт, что a1 ≈ b1 и a2 ≈ b2 (средние значения равны соответственно 0.0402, 0.0569) есть следствие близости σ2-границы доверительной области к
; (I1 = 54). Модель можно считать нормированной. На 3-м этапе ищем границы, положив на вкладке «Константы» Vlog→2. Расчет (<ctrl+g>) даст результат для нормированной модели. После пересчета на исходную модель (<ctrl+i>) получим оценки «стандартных отклонений»: a1 = 0.0403; b1 = 0.0400; a2 = 0.0587; b2 = 0.0551. Поиск границ с точностью eps2 = 10–4 достигнут при W = 10; число обращений (I1) к процедуре вычисления ШФ от 96 до 119. Тот факт, что a1 ≈ b1 и a2 ≈ b2 (средние значения равны соответственно 0.0402, 0.0569) есть следствие близости σ2-границы доверительной области к ![]() , поэтому граница хорошо аппроксимируется эллипсом. Найденный результат интервального оценивания подтверждается вычислениями нелинейным МНК по Гауссу-Зайделю:
, поэтому граница хорошо аппроксимируется эллипсом. Найденный результат интервального оценивания подтверждается вычислениями нелинейным МНК по Гауссу-Зайделю: ![]() .
</ctrl+i></ctrl+g></ctrl+g></ctrl+n>
.
</ctrl+i></ctrl+g></ctrl+g></ctrl+n>
Положив Fi = 200 (соответствует доверительной вероятности 0.95) и повторив действия <ctrl+n, ctrl+g,="" ctrl+i="">, можно видеть, что граница области сильно расширяется и становится несимметричной относительно точки минимума. Это есть следствие нелинейности модели и взаимосвязи ее параметров: </ctrl+n,>
a1 = 0. 534; b1 = 1.204; a2 = 1.567; b2 = 0. 994
Конечный результат удобно представить в виде: ![]() . Его статистическая интерпретация такова, что при доверительной вероятности 0.95 оценки обоих параметров нельзя считать надежными. Это есть следствие малого числа степеней свободы n — m = 1, т. е. мало число наблюдений.
. Его статистическая интерпретация такова, что при доверительной вероятности 0.95 оценки обоих параметров нельзя считать надежными. Это есть следствие малого числа степеней свободы n — m = 1, т. е. мало число наблюдений.
20. Оценивание констант скоростей инактивации биокатализатора.
Зависимость активности y биокатализатора (иммобилизованного фермента) от времени x часто аппроксимируют следующей функцией:
![]() ,(7)
,(7)
где подлежат оцениванию параметры: p1 — доля начальной активности фракции биокатализатора, имеющего константу скорости инактивации p2; p3 — константа скорости инактивации остальной фракции. Требуется найти интервальные МНК-оценки параметров на основании данных табл. 2.
Таблица 2
Исходные данные для модели (7).
|
u |
xu |
yu (активность вдолях от начальной) |
|
1 |
1.0 |
0.42 |
|
2 |
2.0 |
0.30 |
|
3 |
3.0 |
0.25 |
|
4 |
4.0 |
0.17 |
|
5 |
5.0 |
0.17 |
|
6 |
6.0 |
0.15 |
|
7 |
24.0 |
0.13 |
|
8 |
48.0 |
0.07 |
|
9 |
72.0 |
0.06 |
Задача интересна в том отношении, что при p2 ≈ p3 модель (7) становится вырожденной, однопараметрической (т.н. «эффект нуля»); в таких случаях, а также при недостаточно широкой выборке yu(xu) оценивание ее параметров по МНК вызывает трудности.
Решение задачи. Записать процедуру Sub MF(u), приняв: p1→P(1); p2→P(2); p3→P(3); xu →X(u); yu →Y(u); ![]() →F1:
→F1:
Sub MF(u) 'функция-модель инактивации биокатализатора
Dim X1 As Single, P1, P2, P3 As Double
X1 = X(u): P1 = Mp(1)*P(1): P2 = Mp(2)*P(2): P3 = Mp(3)*P(3)
F1 = P1 * Exp(-P2 * X1) + (1 — P1) * Exp(-P3 * X1)
End Sub
Ввести данные табл. 2 на вкладке «Регрессия». На вкладке «Константы» положить m → 3; n → 9; Fi → 4.76. Сначала следует найти вектор ![]() , для чего выбрать Ulog → 1; Vlog → 0; очистить таблицы от результатов предыдущих расчетов (<ctrl+t>). На вкладке «GLSM» ввести начальные оценки, например,
, для чего выбрать Ulog → 1; Vlog → 0; очистить таблицы от результатов предыдущих расчетов (<ctrl+t>). На вкладке «GLSM» ввести начальные оценки, например, ![]() . Поскольку масштаб компонентов
. Поскольку масштаб компонентов ![]() неизвестен, произвести расчеты при
неизвестен, произвести расчеты при ![]() . Запуском программы (<ctrl+g>) будет получен результат (округлено до 3-х знаков):
</ctrl+g></ctrl+t>
. Запуском программы (<ctrl+g>) будет получен результат (округлено до 3-х знаков):
</ctrl+g></ctrl+t>
![]() .
.
Перед поиском границ модель надо нормировать (<ctrl+n>) и повторить расчет (<ctrl+g>). Наконец положить Vlog→2, найти границы (<ctrl+g>) и выполнить переход к исходной модели (<ctrl+i>). Итог: ![]() . Из сравнения с результатами интервального оценивания по методу Гаусса-Зайделя,
</ctrl+i></ctrl+g></ctrl+g></ctrl+n>
. Из сравнения с результатами интервального оценивания по методу Гаусса-Зайделя,
</ctrl+i></ctrl+g></ctrl+g></ctrl+n>
![]() видно, что расчеты по МНК с линеаризацией модели приводят к очень сильным искажениям границ совместной доверительной области. Для более наглядного сопоставления, по программе «GLSM» были вычислены экстремальные отклонения для линейного приближения модели:
видно, что расчеты по МНК с линеаризацией модели приводят к очень сильным искажениям границ совместной доверительной области. Для более наглядного сопоставления, по программе «GLSM» были вычислены экстремальные отклонения для линейного приближения модели:
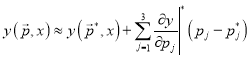 .
.
Получены интервальные оценки ![]() , полностью совпадающие с оценками по методу Гаусса-Зайделя. На рис. 3 показано, как уровень доверительной вероятности сказывается на расхождениях интервальных оценок параметров исходной и линеаризованной моделей (рассчитано по «GLSM» путем варьирования Fi). В полном соответствии с теорией, опыт расчетов с нелинейными моделями показывает, что расхождения тем больше, чем больше нелинейность модели, меньше значимость параметров и больше уровень доверительной вероятности. В большинстве случаев методы линеаризации позволяют более-менее правильно оценивать лишь стандартные отклонения (среднеквадратичные ошибки). В этом отношении алгоритм «GLSM», помимо своей простоты, обладает особым преимуществом.
, полностью совпадающие с оценками по методу Гаусса-Зайделя. На рис. 3 показано, как уровень доверительной вероятности сказывается на расхождениях интервальных оценок параметров исходной и линеаризованной моделей (рассчитано по «GLSM» путем варьирования Fi). В полном соответствии с теорией, опыт расчетов с нелинейными моделями показывает, что расхождения тем больше, чем больше нелинейность модели, меньше значимость параметров и больше уровень доверительной вероятности. В большинстве случаев методы линеаризации позволяют более-менее правильно оценивать лишь стандартные отклонения (среднеквадратичные ошибки). В этом отношении алгоритм «GLSM», помимо своей простоты, обладает особым преимуществом.

Рис. 3. Сечение гиперповерхности ![]() для масштабированной модели (7) вдоль траектории поиска экстремальных границ параметра p2 при различных значениях Fi. Цифры на рисунке: 1 — исходная модель, 2 — линеаризованная модель; 3 — уровень σ2 (Fi = 1/m = 0.333); 4 — уровень 95 %-ой доверительной вероятности (Fi = 4.76); 5 — уровень 99 %-ой вероятности (Fi = 9.28)
для масштабированной модели (7) вдоль траектории поиска экстремальных границ параметра p2 при различных значениях Fi. Цифры на рисунке: 1 — исходная модель, 2 — линеаризованная модель; 3 — уровень σ2 (Fi = 1/m = 0.333); 4 — уровень 95 %-ой доверительной вероятности (Fi = 4.76); 5 — уровень 99 %-ой вероятности (Fi = 9.28)
В заключение рассмотрим решение более сложной задачи.
30. Нахождение ступенчатых констант устойчивости комплексов.
Требуется найти интервальные МНК-оценки параметров βj, (j = 1,… m), следующей математической модели (функция образования Бьеррума):
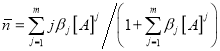 .(8)
.(8)
В ней ![]() – среднее число лигандов A, координированных вокруг центрального катиона M, [A] — концентрация лиганда, βj — суммарная ступенчатая константа устойчивости комплекса состава MAj. Исходными данными являются опытные значения
– среднее число лигандов A, координированных вокруг центрального катиона M, [A] — концентрация лиганда, βj — суммарная ступенчатая константа устойчивости комплекса состава MAj. Исходными данными являются опытные значения ![]() . Особенности задачи состоят в том, что а) исходно функция-модель (8) бывает плохо масштабированной, т. к. величины компонентов вектора параметров
. Особенности задачи состоят в том, что а) исходно функция-модель (8) бывает плохо масштабированной, т. к. величины компонентов вектора параметров ![]() часто различаются между собой на несколько порядков, б) небольшие погрешности опытных данных приводят к большим погрешностям результатов (плохая обусловленность модели). Рассмотрим решение задачи на примере, заимствованном из работы [7] (комплексные аммиакаты Cu2+, табл. 3).
часто различаются между собой на несколько порядков, б) небольшие погрешности опытных данных приводят к большим погрешностям результатов (плохая обусловленность модели). Рассмотрим решение задачи на примере, заимствованном из работы [7] (комплексные аммиакаты Cu2+, табл. 3).
Таблица 3
Исходные данные для модели (8).
|
u |
[A]u |
|
|
1 |
0.203·10–4 |
0.244 |
|
2 |
0.462·10–4 |
0.486 |
|
3 |
1.265·10–4 |
0.959 |
|
4 |
5.35·10–4 |
1.877 |
|
5 |
2.29·10–3 |
2.784 |
|
6 |
8.63·10–3 |
3.437 |
|
7 |
2.265·10–2 |
3.743 |
|
8 |
0.2477 |
4.002 |
Из данных видно, что высшим комплексом в системе является Cu(NH3)42+, поэтому принимаем m = 4.
Решение задачи. Записываем процедуру Sub MF(u), приняв: β1→P(1); β 2→P(2); β 3→P(3); β 4→P(4); [A]u →X(u); ![]() →Y(u);
→Y(u); ![]() →F1:
→F1:
Sub MF(u) ' задача Бьеррума
Dim X1 As Single, P1, P2, P3, P4 As Double
X1 = X(u): P1 = Mp(1) * P(1): P2 = Mp(2) * P(2)
P3 = Mp(3) * P(3): P4 = Mp(4) * P(4)
F1 = (P1 * X1 + 2 * P2 * X1 ^ 2 + 3 * P3 * X1 ^ 3 + 4 * P4 * X1 ^ 4) / _
(1 + P1 * X1 + P2 * X1 ^ 2 + P3 * X1 ^ 3 + P4 * X1 ^ 4)
End Sub
Очищаем таблицы (<ctrl+t>). На вкладке «GLSM» вносим начальное приближение ![]() . На вкладке «Константы» полагаем: m = 4; n = 8; Fi = 6.39; Ulog = 1; Vlog = 0. Запускаем программу поиска S* (<ctrl+g>) и получаем предварительный результат:
. На вкладке «Константы» полагаем: m = 4; n = 8; Fi = 6.39; Ulog = 1; Vlog = 0. Запускаем программу поиска S* (<ctrl+g>) и получаем предварительный результат:![]() ;
; ![]() = 2.27. На вкладке «Регрессия» видно, что результат подгонки неудовлетворителен. Это является следствием плохого масштабирования модели (ДМ коллапсирует, не достигнув минимума). Нормируем модель на данном этапе (<ctrl+n>) и повторяем расчет (<ctrl+g>), получаем для предварительно масштабированной модели:
= 2.27. На вкладке «Регрессия» видно, что результат подгонки неудовлетворителен. Это является следствием плохого масштабирования модели (ДМ коллапсирует, не достигнув минимума). Нормируем модель на данном этапе (<ctrl+n>) и повторяем расчет (<ctrl+g>), получаем для предварительно масштабированной модели: ![]() при
при ![]() = 2.48·10–4. Нормируем модель вторично (<ctrl+n>) и снова выполняем расчет (<ctrl+g>). Получаем
= 2.48·10–4. Нормируем модель вторично (<ctrl+n>) и снова выполняем расчет (<ctrl+g>). Получаем ![]() , модель нормирована. На вкладке «Константы» полагаем Vlog = 2 и программа осуществляет поиск границ (<ctrl+g>). Наконец производим пересчет на исходную модель (<ctrl+i>) и получаем окончательно (записано с точностью до сотых):
, модель нормирована. На вкладке «Константы» полагаем Vlog = 2 и программа осуществляет поиск границ (<ctrl+g>). Наконец производим пересчет на исходную модель (<ctrl+i>) и получаем окончательно (записано с точностью до сотых): ![]() при
при ![]() = 2.48·10–4. Опять-таки, реальные границы доверительной области оказываются несимметричными относительно точки минимума. Верность результата поиска точечных МНК-оценок подтверждается расчетами по Гауссу-Зайделю. Т.о. алгоритм «GLSM» прекрасно справился с решением задачи для исходно плохо масштабированной модели.
</ctrl+i></ctrl+g></ctrl+g></ctrl+n></ctrl+g></ctrl+n></ctrl+g></ctrl+t>
= 2.48·10–4. Опять-таки, реальные границы доверительной области оказываются несимметричными относительно точки минимума. Верность результата поиска точечных МНК-оценок подтверждается расчетами по Гауссу-Зайделю. Т.о. алгоритм «GLSM» прекрасно справился с решением задачи для исходно плохо масштабированной модели.
</ctrl+i></ctrl+g></ctrl+g></ctrl+n></ctrl+g></ctrl+n></ctrl+g></ctrl+t>
Литература:
- Линник Ю. В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. — Л.: Физматгиз, 1962. — 352 с.
- Химмельблау Д. Анализ процессов статистическими методами. — М.: Мир,
- 1973. — 957 с.
- Цибанов В. В. Определение границ совместной доверительной области при нелинейном оценивании параметров физико-химических моделей. // Журн. физической химии. — 1989. — Т. — LXIII. — С. 758–763.
- Химмельблау Д. Прикладное нелинейное программирование. — М.: Мир, 1975. — 534 с.
- Программа минимизации функции многих переменных методом деформируемого многогранника (по Нелдеру и Миду).
- URL: http://tsibanoff.narod.ru/algorythms/simplex.pdf. Посещён 14.11.2017.
- Программа «GLSM». URL: http://tsibanoff.narod.ru/algorythms/glsm.xls. Посещен 14.11.2017.
- Бьеррум Я. Образование аминов металлов в водном растворе. — М.: ИЛ, 1961. — 308 с.
[1] Процедура не затрагивает ![]() и исходные данные регрессии.
и исходные данные регрессии.
[2] Программа испытывалась только в Windows XP SP3.
[3] При задании величины Fi = 1/m, будут найдены границы, в линеаризованной интерпретации отвечающие стандартным отклонениям параметров (среднеквадратичные ошибки).
[4] Если данное окно пустое, то из его главного меню пройти: View > Project Explorer (или нажать
[5] Пример заимствован из [4, стр. 149 ], задача 3.44. Функция-модель характерна взаимосвязью параметров, приводящей в пространстве суммы квадратов к "гиперболическим хребтам".
[6] Установлена в программе по умолчанию.

