В данной статье приведены результаты разработки алгоритма оптимизации изменяемых характеристик двигателей, основанных на принципах обратного пьезоэлектрического эффекта. Приведены используемые в разработке алгоритмы машинного обучения и способы их оптимизации. Разработаны инновационные алгоритмы поэтапной визуализации вычислительных процессов, происходящих в ходе исполнения алгоритма оптимизации изменяемых характеристик двигателей, основанных на принципах обратного пьезоэлектрического эффекта.
Ключевые слова: алгоритмы, ультразвуковой двигатель, пьезоэлектрический эффект, визуализация, вычислительные процессы, машинное обучение
С развитием высоких технологий и повышением сложности проведения вычислений возрастает потребность в качественно новом способе мониторинга их динамически изменяемых результатов.
В целях облегчения восприятия результатов вычислительных процессов используются различные методы визуализации. За счет использования такого подхода можно отойти от исключительно математических представлений вычислений и их результатов к более удобному для восприятия графическому методу отображения. Использование техник визуализации предоставляет пользователю информации значительно более эффективный инструмент для ее мониторинга, контроля и дальнейшего использования.
Огромным источником статистических и математических данных являются коммерческие и некоммерческие компании, использующие в своих разработках и исследованиях методики и алгоритмы машинного обучения. Машинное обучение — один из самых больших разделов направлений научных исследований, занимающихся развитием искусственного интеллекта. Конкретизируя специфику алгоритмов этого направления, немаловажно отметить то, что они способны к автоматическому обучению в ходе обработки информации. Важно отметить, что существует два типа обучения: обучение по прецедентам и индуктивное обучение [1]. Индуктивное обучение базируется на методиках выявления общих закономерностей по конкретным эмпирическим данным. Дедуктивное обучение относится к разряду экспертных методов, используя предварительно сформированные базы знаний. В целом, машинное обучение использует математические, статистические и методы оптимизации. Так же решаются проблемы вычислительной эффективности и переобучения. Учитывая текущую ситуацию в процессе развития инженерных технологий и подходов, машинное обучение является не только теоретическим способом обработки информации, но и имеет широкое применение на практике. Например, в настоящее время на рынке инженерных технологий существует потребность в оптимизации алгоритмов динамического управления мощностью двигателей разных типов, в том числе двигателей, основанных на принципах обратного пьезоэлектрического эффекта [3–6]. В данной статье продемонстрированы результаты действия разработанного в ходе исследования нового подхода к визуальному отображению результатов исполнения алгоритмов машинного обучения с целью оптимизации процесса динамического изменения мощностных характеристик двигателей.
В целях понимания специфики визуализации вычислительных процессов рассмотрим некоторые способы использования алгоритмов машинного обучения и визуализацию их результатов.
Одним из самых простых и эффективных алгоритмов машинного обучения является метод наименьших квадратов. Метод наименьших квадратов используется в качестве способа реализации линейной регрессии. Метод наименьших квадратов заключается в проведении оценки, в ходе которой минимизируется сумма квадратов отклонений наблюдаемых значений зависимой переменной от значений, предсказанных моделью [2]. Оценка наименьших квадратов параметра q рассчитывается проведением минимизации функции Q по Ɵ, где Q:
![]()
На рисунке 1 продемонстрировано графическое отображение результатов вычислений по методу наименьших квадратов в общем случае.
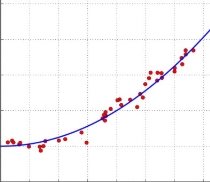
Рис. 1. Пример отображения результатов вычислений по методу наименьших квадратов
Другим эффективным алгоритмом машинного обучения является метод опорных векторов. Этим термином можно назвать семейство алгоритмов, использующихся для задач классификации и регрессионного анализа. Задачи классификации такого типа имеют достаточно широкий диапазон применений. К примеру, метод опорных векторов используется в распознавании образов. На рисунке 2 продемонстрирована визуализация результата работы алгоритма на массиве информации. На рисунке 2 видно, что с помощью оптимизационной технологии визуализации результатов вычислений с помощью метода опорных векторов легко разделить объекты на два класса. В данном случае продемонстрирован пример так называемой бинарной классификации, так как результирующий набор данных содержит только два вида объектов. В реальной практике встречаются задачи, в которых присутствует множество видов объектов. В таком случае это — мультиклассовая классификация. Более того, еще перед началом проведения вычислений могут быть известны классы, к которым относятся исследуемые объекты. В таком случае, задача носит название обучения с учителем, а заранее идентифицированные данные — обучающей выборки.
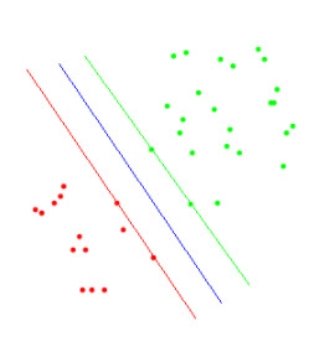
Рис. 2. Отображение результатов вычисления с использованием метода опорных векторов
Несмотря на то, что применение метода опорных векторов на сегодняшний день достаточно хорошо изучено и имеет широкое распространение в большом количестве технологий, существуют специальные сферы инженерии, требующие большей оптимизации и точности вычислительных процессов. Более того, появляются новые технологии, в которых возможно применение данного метода в целях увеличения эффективности производства и использования новых технологических решений. Например, в целях параметризации данных и составления обучающей выборки, в работе программного обеспечения, регулирующего мощность пьезодвигателей, используется оптимизированная версия данного алгоритма. Примеры двигателей, основанных на принципах обратного пьезоэлектрического эффекта, и применяющихся в совершенно разных областях инженерии, изображены на рисунках 3–4.

Рис. 3. Пьезодвигатель для объектива с автофокусом

Рис. 4. Пьезодвигатель для привода шарового крана
Одним из наиболее распространенных методов машинного обучения является метод главных компонент. Этот метод — статистическая процедура, использующая ортогональное преобразование, с целью уменьшения размерности данных с наименьшими возможными потерями информации. С помощью техник визуализации алгоритма построен график, изображенный на рисунке 5.
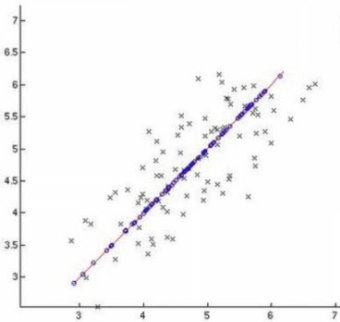
Рис. 5. Пример визуализации результатов вычисления методом главных компонент
Использование метода главных компонент имеет четыре разновидности:
- Аппроксимация данных линейными многообразиями меньшей размерности
- Поиск подпространства меньшей размерности, в ортогональной проекции на которой разброс данных максимален
- Поиск подпространства меньшей размерности, в ортогональной проекции на которой среднеквадратичное расстояние между точками максимально
- Построение для данной многомерной случайной величины ортогонального преобразования координат, в результате которого корреляции между отдельными координатами обращаются в ноль
К примеру, в целях оптимизации средств визуализации процессов, проистекающих в ходе управления мощностью двигателей, основанных на принципах обратного пьезоэлектрического эффекта, в ходе исследования использовалась первая разновидность метода главных компонент — аппроксимация данных линейными многообразиями меньшей размерности. Такой алгоритм оперирует конечными множествами данных. Английский математик Карл Пирсон в 1901 году впервые разработал алгоритм, решая задачу наилучшей аппроксимации конечного множества точек прямыми и плоскостями.
Основная задача данного исследования заключается в создании методов и средств визуализации процессов, проистекающих в ходе динамического управления характеристиками пьезодвигателей. Более того, в целях оптимизации выполнения такого рода процессов, необходимо разработать специализированное программное обеспечение, основанное на эффективных и прогрессивных алгоритмах машинного обучения. Такие оптимизации и создание средств служат для того, чтобы автоматизировать процесс мониторинга состояния двигателя. Более того, процесс мутации параметров должен быть автоматизирован, соответственно должен обладать способностью к автоматическому обучению, учитывая совокупность предыдущих измерений и метаморфоз изменяемых характеристик двигателя.
В разработанном алгоритме используются описанные выше алгоритмы машинного обучения с измененными характеристиками в части формирования обучающей выборки. Оптимизации разработаны в целях ускорения процесса обучения алгоритма, что, в свою очередь, значительно повышает надежность принимаемых алгоритмом решений относительно метаморфоз изменяемых параметров пьезодвигателей. В ходе исследования возможных путей оптимизации алгоритма, установлено, что на первом этапе обработки данных о работе двигателя, которые получены в процессе мониторинга его работы, эффективным является использование метода анализа главных компонент. Это подготавливает качественную выборку данных для последующей обработки. На втором этапе работы алгоритма, используя метод опорных векторов, удается классифицировать данные по признаку «релевантный» \ «нерелевантный». Этот процесс происходит в рамках подготовки обучающих данных для подготовки финального решения об изменении того или иного параметра двигателя. В целях контроля и мониторинга работы алгоритма на каждом этапе происходит фиксация результата и сохранения его в базу данных. Более того, контроллер имеет возможность использовать режим просмотра визуального отображения результатов вычислений на каждом шаге обработки входящих данных. Визуальное представление вычислительных процессов и их результатов значительно повышает качество и эффективность мониторинга работы алгоритма и анализа исторических данных.
В целях анализа эффективности разработанного алгоритма контроля изменяемых характеристик двигателей, основанных на принципах обратного пьезоэлектрического эффекта, и оптимизаций существующих алгоритмов машинного обучения приведем в пример двигатель N-422. На рисунке 6 изображены габаритные и присоединительные размеры используемого двигателя.
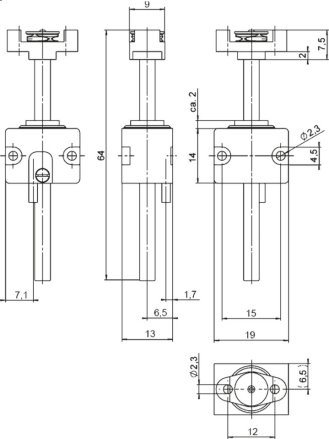
Рис. 6. Габаритный чертёж N-422.50. Размеры указаны в мм.
На рисунке 7 изображен двигатель N-422.50.

Рис. 7. Внешний вид пьезодвигателя N-422.50
Рекомендованным к использованию вместе с указанной серией пьезодвигателей является изображенный на рисунке 8 контроллер E-870.

Рис. 8. Контроллер PIShift серии E-870
В таблице 1 приведены значения характеристик двигателя при понижении рабочего напряжения до 46.75В и 46.0В в сравнении с рабочими частотами.
Таблица 1
Результирующие данные работы разработанного алгоритма
|
Потребляемая мощность (Вт) |
Рабочее напряжение (В) |
Частота шага (кГц) |
Максимальная скорость (мм/сек.) |
Максимальное толкающее/тянущее усилие (Н) |
Максимальное удерживающая сила (Н) | |
|
Стандарт |
30 |
48 |
20 |
5 |
7 |
10 |
|
Метаморфоза — стадия 1 |
29.5 |
46.75 |
19.98 |
5 |
7 |
10 |
|
Метаморфоза — стадия 2 |
28.8 |
46.0 |
19.94 |
5 |
7 |
10 |
Анализируя значения изменяемых параметров, полученных на двух этапах — метаморфозе № 1 и метаморфозе № 2, можно заключить, что алгоритм ведет себя предсказуемо и крайне эффективно. Данный вывод базируется на факте сохранения параметров скорости, толкающего усилия и удерживающей силы неизменными в условиях деградации подаваемого напряжения. Стоит отметить снижение потребляемой мощности на обеих стадиях в рамках допустимого, что гарантирует сохранение бесперебойной работы устройства. Учитывая приведенные данные можно заключить, что разработанный алгоритм обучается на полученных в ходе мониторинга данных и производит точечные изменения характеристик двигателя. Применяя указанные в данной статье методы визуализации вычислительных процессов, легко получить визуально-графическое представление работы алгоритма на каждом его шаге и оценить результаты его работы. Стоит отметить эффективность разработанных алгоритмов визуального отображения и самого оптимизационного алгоритма с точки зрения асимптотической сложности.
С развитием технологий, в современном мире все большей актуальностью обладают разработки и оптимизации в области двигателей, основанных на принципах обратного пьезоэлектрического эффекта. Более того, разработка легких для восприятия визуализаций вычислительных процессов оптимизации изменяемых характеристик двигателей являются также крайне актуальной. Изучение и оперирование данными, представленными в динамическом и графическом виде, значительно сокращают издержи при мониторинге и контроле за процессами. Разработанные в ходе данного исследования алгоритмы и методы визуализации вычислительных процессов и алгоритм оптимизации изменяемых характеристик подходят для использования в тандеме со всеми распространенными видами пьезодвигателей, что делает их универсальным средством повышения эффективности их работы и контроля их производительности [7].
Литература:
1. Дональд Эрвин Кнут, Искусство программирования. Том 1. Основные алгоритмы. — СПб.: Вильямс, 2015. — 720 с.
2. Томас Х. Кормен, Чарльз И. Лейзерсон, Алгоритмы. Построение и анализ. — СПб.: Вильямс, 2016. — 1328 с.
3. Burov, Piezoelectric step motor. -United States Patent 6,242,849, June 5, 2001.
4. Uchino, Piezoelectric motor and method of exciting an ultrasonic traveling wave to drive the motor. -United States Patent 7,095,160, August 22, 2006
5. Moteki, Rotary drive device. -United States Patent 7,116,037, October 3, 2006.
6. Vyshnevskyy, Method for operating a piezoelectric motor, and piezoelectric motor comprising a stator in the form of a hollow-cylindrical oscillator. -United States Patent 7,218,031, May 15, 2007.
7. Рыжов, С. С. Система управления пьезодвигателем — Россия, Единый депозитарий результатов интеллектуальной собственности, свидетельство № 218.016.2Е89–15 марта 2018.

