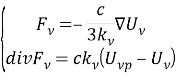Рассматривается метод ускорения расчета параметров переноса селективного излучения при моделировании задач механики высокотемпературных сред. Предложен новый метод решения задачи, основанный на функции вывода в нечеткой системе Такаги-Сугено. Приведена оценка эффективности по точности и скорости вычисления распределения характеристики в задачах радиационного переноса.
Ключевые слова: моделирование, метод, ускорение, радиационный перенос, приближенное отображение, приближенное распределение.
Введение
При решении современных задач астрофизики, плазмодинамики, физики газового разряда значительное внимание приходится уделять правильному учету радиационного переноса в условиях сложного дискретно-непрерывного спектрального состава. При этом значительные вычислительные ресурсы тратятся на получение информации о спектральной зависимости потоков излучения. В этой ситуации актуальной задачей является сокращение машинного времени на вычисления. Выполнение данной задачи возможно в случае обеспечения предварительного формирования массивов данных на основе точных квантово-механических и энергетических расчетов дивергенции интегрального по спектру потока излучения в привязке к фиксированным температурным распределениям.
В ходе решения уравнения энергии аппроксимация на полученном массиве данных позволяет получить существенный выигрыш по времени.
- Формулировка задачи построения приближенного отображения
Пусть ![]() и
и ![]() — дискретно-непрервывные пространства над
— дискретно-непрервывные пространства над ![]() . Считаем, что пространство G имеет функциональную зависимость от пространства F, если для каждой входной функции
. Считаем, что пространство G имеет функциональную зависимость от пространства F, если для каждой входной функции ![]() в F существует одно и только одно соответствие g на выходном пространстве G. Целью данной работы является разработка метода получения выходного распределения g при известном наборе функциональных пространств и входной функции f. Сформулируем решение данной задачи на основе функции вывода в системе нечеткой логики Такаги-Сугено.
в F существует одно и только одно соответствие g на выходном пространстве G. Целью данной работы является разработка метода получения выходного распределения g при известном наборе функциональных пространств и входной функции f. Сформулируем решение данной задачи на основе функции вывода в системе нечеткой логики Такаги-Сугено.
- Способ получения приближенного отображения между двумя функциональными пространствами
Идея функции вывода нечеткой модели Такаги-Сугено заключается в том, что за счет использования систем нечетких правил оказывается возможным, не выходя за рамки линейных зависимостей, учитывать то, что влияние объясняющих переменных на объясняемые при различных условиях может быть разным [1] [2]. В системе вывода Такаги-Сугено четкое значение переменной вывода вычисляется следующей формулой:
![]() (1)
(1)
где ![]() — коэффициент достоверности k-гo правила (или уровень зависимости).
— коэффициент достоверности k-гo правила (или уровень зависимости).
Т. к. в нашей задаче распределение в выходном пространстве имеет зависимость со всех входных распределений, следует учитывать эти зависимости как правила, таким образом, они имеют свой уровень зависимости от точного расчета [3].
Процесс построения приближенного распределения ведется итерационно. Каждое правило имеет следующий вид:
![]() (2)
(2)
где![]() — номер правила;
— номер правила;
![]() оценка зависимости между двумя распределениями в одном пространстве;
оценка зависимости между двумя распределениями в одном пространстве;
![]() — функция аппроксимации,
— функция аппроксимации,![]() .
.
Пусть ![]() и
и ![]() — входная функция в
— входная функция в ![]() и её отображение в
и её отображение в ![]() соответственно. Коэффициенты достоверности
соответственно. Коэффициенты достоверности ![]() -го элемента k-гo правила вычисляется общей формулой [4]:
-го элемента k-гo правила вычисляется общей формулой [4]:
![]() (2)
(2)
В результате приближенное отображение ![]() -го элемента равно:
-го элемента равно:
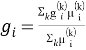 (3)
(3)
Для анализа точности метода в качестве критериев при проведении итерационного процесса используется среднеквадратичная ошибка прогноза RMSE, которая вычисляется по следующей формуле:
![]() (4)
(4)
где ![]() — расчёт точного отображения функции
— расчёт точного отображения функции ![]() в
в ![]() .
.
- Схема поиска выходного приближенного распределения
Приведена схема вычисления приближенного распределения (рис. 1).
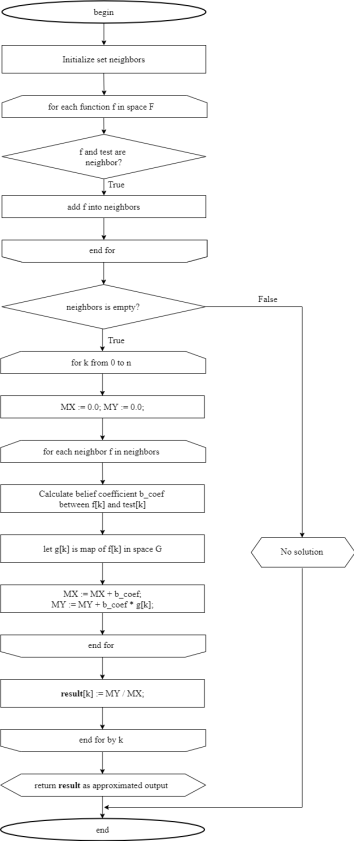
Рис. 1. Схема вычисления приближенного распределения
Замечание:
− на входе задаётся набор ![]() , обозначающий исходное пространство;
, обозначающий исходное пространство;
− ![]() — исходное распределение,
— исходное распределение, ![]() является выходным приближенным распределением;
является выходным приближенным распределением;
− коэффициент достоверности b_coef и приближенное значение выходной функции могут быть вычислены линейным или логарифмическим алгоритмом;
− при пустом множестве соседних элементов процесс вычисления приближенного распределения не выполняется. На практике необходимо подбирать условие так, чтобы множества соседних элементов имели хотя бы один элемент.
- Применение разработанного метода взадаче радиационного переноса
В данном разделе рассматривается применение нового метода для повышения дифференциальных приближений к решению задачи определения радиационных характеристик в задачах радиационного переноса цилиндрической фигуры. Решение прямым (точным) методом является неэффективным и требует объемных вычислений [4] [5] [6].
Уравнение радиационного переноса имеет следующий вид [7]:
|
|
(5) |
Дивергенция потока излучения вычисляется по формуле:
|
|
(6) |
Здесь ![]() — частота,
— частота, ![]() плотность излучения, представляющая собой интеграл от интенсивности излучения
плотность излучения, представляющая собой интеграл от интенсивности излучения ![]() по всем направлениям цилидрического пространства
по всем направлениям цилидрического пространства ![]() ;
; ![]() и
и ![]() определяют плотность и интенсивность равновесного излучения;
определяют плотность и интенсивность равновесного излучения; ![]() спектральный поток излучения и
спектральный поток излучения и ![]() соответственно частная дивергенция потока излучения;
соответственно частная дивергенция потока излучения;![]() коэффициент поглощения и
коэффициент поглощения и ![]() – функция распределения температурного профиля.
– функция распределения температурного профиля.
Рассмотрим решение данной задачи разработанным методом приближенного отображения. На входе программы принимает температурный профиль T, пространство дивергенции потока D (см. рис. 2).
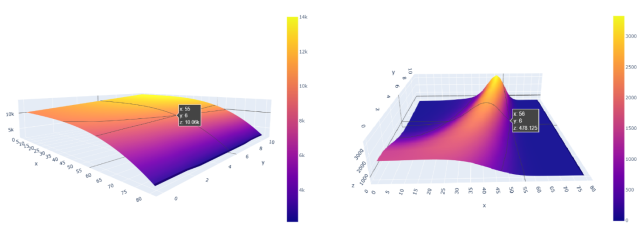
Рис. 2. Двумерное представление пространств температуры (слева) и дивергенции потока (справа)
- Результаты вычисления иэкспериментов
Проведены расчеты приближенного распределения дивергенции потока при заданном распределении температуры с помощью распараллеливания (Рис.3). Показывается хорошее качество приближенного распределения. Выходная функция стремится к точным, её абсолютная ошибка для всех точек в приближенной функции равна 0.1–5 %.
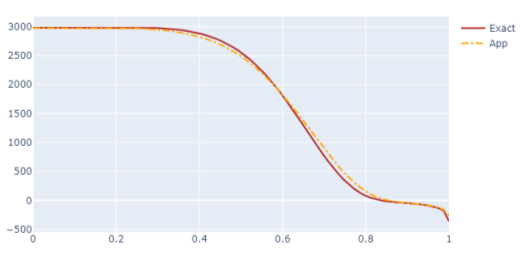
Рис. 3. Представление расчёта дивергенции потока методом приближенного отображения по сравнению с точным методом при распараллеливании процессов
Проведен расчёт времени реализации распараллеливания процессов вычисления приближенного отображения с использованием технологии OpenMP[8] [9].
Таблица 1
Расчёт времени вычисления приближенного распределения при распараллеливании процессов (количество потоков (0, 4, 8)
|
Без параллеливания |
4 потока |
8 потоков | |
|
Время (mс) |
8.40702 |
1.99991 |
0.99995 |
При распараллеливании процессов наш метод работает быстрее, чем в обычной среде. Из результата эксперимента можем сделать вывод о том, что разработанный метод практически ускорит процесс в ![]() раз при использовании
раз при использовании ![]() потоков.
потоков.
Результат сравнения времени вычисления распределения характеристик разработанным и точным методами показан на рисунке 4.
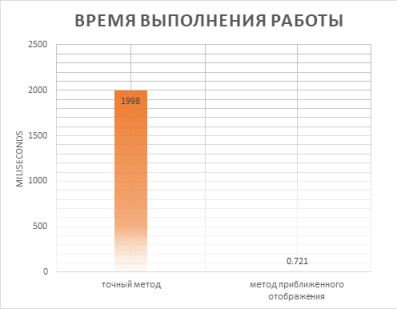
Рис. 4. График расчёта времени вычисления двух методов: точный метод и метод приближенного отображения
Видно, что разработанный нами метод занимает меньше времени на вычисления. Это можно объяснить тем, что в прямом методе требуется огромный объём вычислений, сложность этого алгоритма есть ![]() . Метод приближенного отображения имеет сложность
. Метод приближенного отображения имеет сложность ![]() в худшем случае, при
в худшем случае, при ![]() он приближается к
он приближается к ![]() . Разработанный метод выполняется со сложностью
. Разработанный метод выполняется со сложностью ![]() в реальности, т. е. он ускоряет процесс вычислений на три порядка.
в реальности, т. е. он ускоряет процесс вычислений на три порядка.
Эксперименты показывают, что качество аппроксимации функции является практически надежным. Вследствие применения данного подхода реализуется ускорение вычисления дифференциальных приближений в задачах радиационного переноса.
Заключение
На основе функции вывода в нечеткой логике разработан метод приближенного отображения температурного профиля на пространство распределения дивергенции потока излучения применительно к задачам моделирования процессов в цилиндрических объемах высокотемпературных сред. Показано, что разработанный метод дает результаты, отличающиеся от полученных точным методом в пределах 4–5 %. При этом быстродействие метода приближенного отображения почти на три порядка выше прямого метода.
Литература:
- Ю. Н. Хижняков. Алгоритмы нечеткого, нейронного и нейронечеткого управления в системах реального времени. // Издательство Пермского национального исследовательского политехнического университета, 2013.
- Е. В. Кочергин, Т. М. Леденева, А. В. Алтухов. Об одном подходе к аппроксимации функции с помощью систем Takagi-Sugeno // Воронежский государственный университет, 2008.
- Butkiewicz B., Rutkowski L., Kacprzyk J. Simple modification of Takagi-Sugeno Model // Neural Networks and Soft Computing. — № 11, 2003.
- R. E. Bellman, L. A. Zadeh Decision making in a fuzzy environment. Management Science, 17, 141–164, 1970.
- Градов В. М., Желаев И. А., Коробков С. С. Математическое моделирование и экспериментальное исследование процессов в разрядных импульсно-периодических источниках излучения с ксеноновым наполнением. Научно-технический вестник Поволжья 2018 — № 2.
- Gradov V. M., Gavrish S. V., Rudakov I. V. Simulation of electrophysical processes in pulse-periodic tubular sources of powerful infrared radiation with sapphire shells. Vestn. Mosk. Gos. Tekh. Univ. im. N. E. Baumana, Priborostr. [Herald of the Bauman Moscow State Tech. Univ., Instrum. Eng.], 2017, no. 6, pp. 130–145 (in Russ.). DOI: 10.18698/0236–3933–2017–6–130–145
- В. М. Градов. Программно-математическое обеспечение для научных исследований систем с доминирующей ролью радиационных процессов. ISSN 0236–3933. Вестник МГТУ им. Н. Э. Баумана. Сер. “Приборостроение”. 2012.
- А. С. Антонов. Параллельное программирование с использованием технологии OpenMP.// Издательство МГУ, 2009.
- Tim Mattson, Larry Meadows. A “Hands-on” Introduction to OpenMP./ https://www.openmp.org/wp-content/uploads/omp-hands-on-SC08.pdf