В данной статье проанализированы характерные проблемы вычислений с высокой точностью при использовании гибридных вычислительных систем на базе графических процессоров NVIDIA. Выявлены характерные особенности графических процессоров, способные влиять на точность вычислительного эксперимента. В результате данные особенности привносят расхождения в результаты численных экспериментов. С подобными расхождениями численных результатов автор столкнулся в ходе работы над параллельной реализацией полу-Лагранжевого метода решения начально-краевой задачи для уравнения неразрывности. На основе проведенного исследования автором предлагаются некоторые обходные пути для уменьшения разницы в численных результатах, возникающей вследствие разной аппаратной архитектуры центрального и графического процессоров.
Введение
Проведение вычислительного эксперимента является неотъемлемой частью исследований в области численного моделирования. Одной из важнейших характеристик любого вычислительного эксперимента является точность полученных результатов. Однако для получения точных результатов расчетов вычислителю необходимо хорошо понимать, как устроена работа с числами с плавающей точкой на программном и аппаратном уровнях. Множество действительных чисел является не только бесконечным, но и непрерывным, а память вычислительной системы (ВС) ограничена, таким образом, всегда найдется действительное число, которое не будет иметь точного представления в памяти системы. Числа с плавающей точкой были предложены как один из способов представления действительного числа в памяти, который является компромиссом между точностью и диапазоном принимаемых значений [3, 4].
Исследования, связанные с проблемой представления чисел с плавающей точкой, ведутся с 70-х годов ХХ столетия, и большинство технических вопросов их арифметики в рамках классических ВС успешно решены. Однако современные параллельные архитектуры, особенно гибридные, основанные на совместном использовании CPU и GPU, вновь обострили проблему точности вычислений и сравнимости получаемых результатов численных экспериментов в разных аппаратных и программных конфигурациях.
Действительно, при использовании гибридных ВС наряду с фундаментальной проблемой неассоциативности операций над числами с плавающей точкой, которая характерна для классических параллельных ВС, на результат вычислений влияет аппаратная архитектура GPU.
В ходе работы над параллельной реализацией полу-Лагранжевого метода решения начально-краевой задачи для уравнения неразрывности [2] автором было выявлено расхождение численных результатов решения, полученных при использовании последовательной и параллельной версии программы. Параллельная версия алгоритма предполагала использование GPU и технологию NVIDIA CUDA в качестве вычислительного сопроцессора. В итоге была предпринята попытка систематизировать причины появления численных расхождений в результатах вычислительных экспериментов при использовании графических процессоров и процессоров общего назначения. Дополнительную информацию по данной проблеме можно получить в источниках [1, 5].
Данная статья описывает некоторые общие причины появления несоответствий в численных результатах при использовании гибридных вычислительных систем. В качестве вычислительного стенда применялся вычислительный узел ИВМ СО РАН Flagman RX240T8.2 на базе графических процессоров Tesla C2050, имеющий 2 шестиядерных процессора Intel Xeon X5670 и 8 GPU NVIDIA Tesla C2050 [9].
Стандарт IEEE754
Стандарт IEEE 754 разработан международной ассоциацией IEEE (Institute of Electrical and Electronics Engineers) и используется для представления чисел с плавающей точкой в двоичном коде. Данный стандарт является наиболее распространённым для вычислений с плавающей точкой, он используется многими микропроцессорами и логическими устройствами, а также программными средствами. Стандарт включает арифметические операции (сложение, вычитание, умножение, деление), вычисление квадратного корня, остатка, сравнения и операции преобразования типов. Результаты данных операций будут гарантированно одинаковы для всех реализаций стандарта при одинаковом формате хранения числа и режиме округления [1].
Несмотря на наличие стандарта IEEE 754, проблема переносимости, а также проблема воспроизводимости численных расчетов, не были решены полностью. Существует несколько причин, которые влияют на точность вычислений, а также, в случае применения параллельных вычислительных систем, на воспроизводимость численных результатов [1]:
1. Порядок выполнения арифметических операций и сопутствующие округления.
2. Проблема приближенного вычисления математических функций.
3. Неполная поддержка последних версий стандарта IEEE 754 как со стороны GPU, так и со стороны CPU.
4. Совместное использование аппаратных технологий, предполагающих применение расширенной и одинарной/двойной точности.
Остановимся на каждой из причин подробнее.
Порядок выполнения арифметических операций
Исследование ошибок округления всегда осложняется тем фактом, что данные ошибки в результате приводят к качественному отклонению от нормального поведения. Операции сложения и умножения чисел с плавающей точкой обладают свойством коммутативности, однако в то же время не обладают свойствами ассоциативности и дистрибутивности [3, 4]. На рис. 1 представлен пример, показывающий отсутствие ассоциативности операции сложения при работе с числами с плавающей точкой.
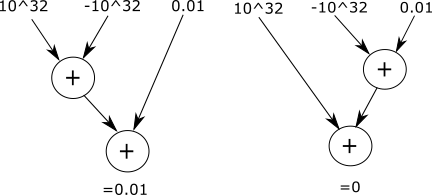
Рис. 1. Неассоциативность операции сложения при работе с числами с плавающей точкой
Проблема отсутствия ассоциативности и дистрибутивности при работе с числами с плавающей точкой особенно остро встает при использовании параллельных вычислительных систем. Очевидно, что при наличии нескольких вычислительных потоков невозможно гарантировать определенный порядок выполнения арифметических операций. Причем наиболее явно данная проблема проявляет себя при использовании именно GPU для проведения расчетов в силу массивно-параллельной архитектуры последних.
Аппаратная архитектура GPU является по сути последовательно-параллельной. Данные разбиваются на блоки, где каждому элементу данных соответствует определенный вычислительный поток. Число потоков в каждом блоке, как и число блоков, регулируется при запуске вычислительного ядра (рис. 2). Каждый блок распределяется планировщиком на свой вычислительный потоковый процессор путем постановки блока в очередь задач потокового процессора. Соответственно блоки на каждом процессоре выполняются последовательно, тогда как каждый потоковый процессор независимо обрабатывает каждый блок. Потоки внутри каждого блока исполняются параллельно. Данные особенности архитектуры приводят к тому, что от запуска к запуску результаты вычислений могут отличаться, поскольку значительно меняется порядок выполнения операций. Более подробно с архитектурой GPU компании NVIDIA можно ознакомиться в [10].
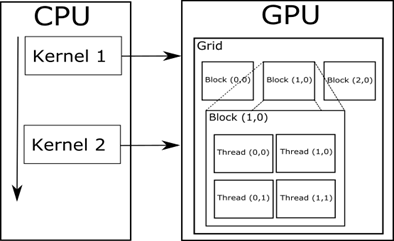
Рис. 2. Программная модель работы вычислительного ядра NVIDIA CUDA
Данную особенность аппаратной архитектуры GPU необходимо учитывать при оценке полученных численных результатов расчетов. В целях отладки параллельной версии алгоритма автором рекомендуется запускать вычислительное ядро с одним блоком и одним потоком в блоке. В этом случае гарантируется отсутствие недетерминированности при вычислениях вследствие аппаратных особенностей GPU, поскольку в подобном режиме вычисления производятся в однопоточном режиме.
Проблема приближенного вычисления математических функций
В отличие от простых арифметических операций, задача получения лучшего значения числа с плавающей точкой при использовании математических функций несколько сложнее. Данная проблема получила название «дилеммы составителя таблиц» [1].
Дилемма заключается в следующем. Для того чтобы гарантировать корректно округленный результат, в общем случае недостаточно рассчитать значение функции при фиксированной высокой точности. Сколько бы высокую точность не взяли, всегда найдутся редкие случаи, в которых ошибка в высокоточном результате повлияет на округление при низкой точности.
Существует два способа решить данную дилемму. Первый способ состоит в том, чтобы привести математическое доказательство корректности результата каждой отдельной функции. Однако, принимая в расчет крайнюю сложность подобных доказательств, производители численных библиотек применяют другой подход, при котором для каждой функции определяются границы относительной ошибки на указанном диапазоне принимаемых значений. Для описания границ относительной ошибки применяют понятие ulp (unit in the last position). Например, функция sin(x), которая возвращает результат двойной точности, гарантирует, что результат не будет превышать 2 ulp. Другими словами это означает, что разница между вычисленным результатом и точным математическим значением не будет превышать ±2 по отношению к позиции последних значащих битов дробной части результата в виде числа с плавающей точкой [1].
В листинге 1 представлен исходный код программы, которая вычисляет значение косинуса для заданного значения аргумента.
#include "math.h"
#include "stdio.h"
int main()
{
volatile float x = 5992555.0;
printf("cos(%f): %.10g", x, cos(x));
return 0;
}
Листинг 1. Исходный код вычисления косинуса числа
На рис. 3 представлен результат выполнения программы. Как видно, при компиляции примера для 32-битной системы значение косинуса равно 3.320904692e-07, тогда как для 64-бит значение равно 3.320904615e-07. Данный пример показывает, что изменение битности вычислительной программы влияет на конечный результат расчетов даже при условии использования одинаковой библиотечной функции cos(x) [1]. Таким образом, при проведении расчетов следует внимательно следить за тем, в какой битности предполагается исполнение вычислительной программы.

Рис. 3. Влияние опций компиляции на результат вычислений функции cos(x).
Первая строка показывает компиляцию для 32 бит,
третья строка показывает компиляцию для 64 бит
Таким образом, одной из причин расхождений численных результатов вычислений на CPU и GPU, которые автор получил в ходе работы над параллельной реализацией полу-Лагранжевого метода решения начально-краевой задачи для уравнения неразрывности [2], является присутствие отличий в реализации стандартных математических функций в библиотеках для NVIDIA CUDA и стандартной библиотеки GNU C Library. К сожалению, дать какие-то конкретные рекомендации по устранению данного расхождения не представляется возможным.
Функции, скомпилированные для GPU, будут использовать математическую библиотеку NVIDIA CUDA, тогда как для вычислений на CPU будут использоваться математические библиотеки, реализованные для использования на CPU (например, GNU C Library для Linux). Поскольку данные реализации развиваются независимо и обе не могут гарантировать корректно округленного результата, расчеты на GPU и CPU всегда будут немного отличаться [1].
Неполная поддержка последних версий стандарта IEEE 754
Одним из наиболее важных факторов, который может влиять на расхождение результатов численного эксперимента на CPU и GPU, является разница в поддержке разных версий стандарта IEEE 754 для разных вычислительных устройств.
В ревизии стандарта IEEE 754-2008, который был принят в 2008 г., была включена операция Fused Multiply-Add (FMA, операция умножение-сложение) [7]. При использовании данной операции два числа умножаются и складываются за один такт, т.е. x = a * b + c. Преимущество операции FMA для чисел с плавающей точкой заключается в том, что в процессе ее применения происходит одно округление вместо двух. Другими словами, если принять, что операция rn – это операция округления, то FMA производит вычисления по формуле x = rn (a * b + c), вместо x = rn (rn (a * b) + c). Таким образом, результаты вычислений при использовании FMA имеют более высокую точность [1].
Графические процессоры компании NVIDIA имеют аппаратную поддержку стандарта IEEE-754-2008 для чисел с плавающей точкой одинарной и двойной точности, начиная с версии compute capability 2.0. Таким образом, поддержкой данной операции обладают чипы серии GF100 и выше. Первые версии данных чипов были выпущены 12 апреля 2010 г. [8]. В то же время первые современные коммерческие CPU с аппаратной поддержкой данной операции появились лишь в 2011 г. (AMD Bulldozer) и в 2013 г. (Intel Haswell) [6]. При сравнении результатов расчетов GPU и CPU следует учитывать разницу в степени поддержки различных ревизий стандарта IEEE-754.
Совместное использование аппаратных технологий, предполагающих
применение расширенной и двойной/одинарной точности
На аппаратных платформах, которые поддерживают наборы инструкций x87 и SSE, могут возникать расхождения в численных результатах. В то время как программная реализация NVIDIA CUDA также, как и SSE, использует только наборы инструкций, оперирующие числами с плавающей точкой одинарной и двойной точности, набор инструкций x87 использует операции, которые зачастую предполагают использование повышенной 80-битной точности [1]. Таким образом, при использовании архитектуры x87 результаты вычислений могут зависеть от того, были ли промежуточные результаты вычислений сохранены в 80-битных регистрах или в основной оперативной памяти. Значения, сохраненные в оперативной памяти, округляются до стандартной одинарной или двойной точности, в то время как числа, хранящиеся в регистрах, находятся в расширенной 80-битной точности [1]. Также следует заметить, что по умолчанию компиляция в 32-битный код будет использовать набор инструкций x87 (при наличии аппаратной поддержки), тогда как набор инструкций SSE используется по умолчанию при 64-битной компиляции.
Сравнивая результаты расчетов на CPU и GPU, следует убедиться в том, что при расчете на CPU не использовался набор инструкции x87. Поскольку набор инструкций SSE следует стандарту IEEE 754 для чисел с плавающей точкой, следует использовать данный набор инструкций при проведении расчетов на CPU [1].
Заключение
Одинаковые входные данные могут возвращать одинаковый результат для отдельных операций стандарта IEEE 754 для заданной точности вычислений и режима округления на CPU и GPU. Однако, как описано в статье, крайне сложно исполнить операции в одинаковом порядке, используя одинаковый набор инструкций, на CPU и GPU. Основные причины, приводящие к тому, что один набор инструкций не может быть одинаково исполнен на CPU и GPU, следующие.
1. Параллельные алгоритмы меняют порядок операций.
2. CPU может рассчитывать результаты, «за кулисами» используя большую точность.
3. GPU имеет аппаратную поддержку FMA, которая включена по умолчанию.
4. Корректное округление общих математических функции не регулируется стандартом IEEE 754.
В процессе портирования программы вычислений с CPU на GPU определенно имеет смысл использовать результаты x86 CPU как эталонные. Однако разница в численных результатах между GPU и CPU не является автоматическим доказательством некорректности расчетов на GPU. Любые расхождения в расчетах должны быть аккуратно изучены, принимая в расчет материал, представленный в статье.
Работа выполнена при финансовой поддержке РФФИ (грант № 14-01-31203).
Литература:
- Whitehead N. Precision & Performance : Floating Point and IEEE 754 Compliance for NVIDIA GPUs / N. Whitehead, A. Fit-florea – Santa Clara , 2011. – 7 p.
- Efremov A.A., Karepova E.D., Shaydurov V.V., Vyatkin A.V. A Computational Realization of a Semi-Lagrangian Method for Solving the Advection Equation A.V. / A.A. Efremov, E.D. Karepova, V.V. Shaydurov, A.V. Vyatkin. J. Appl. Math. – 2014. – Vol. 2014.
- Вержбицкий В.М. Основы численных методов / В.М. Вержбицкий. – М.: Высш. школа, 2002. – 840 с.
- Воеводин В.В. Вычислительные основы линейной алгебры / В.В. Воеводин. – М.: Наука, 1977. – 304 c.
- Forsythe G. Pitfalls of computation, or why a math book isn’t enough // Amer. Math. Mon. – 1970. – P. 931–956.
- Multiply–accumulate operation [Электронный ресурс]. URL: http://en.wikipedia.org/wiki/Multiply%E2%80%93accumulate_operation (дата обращения: 21.03.2015).
- 754-2008 – IEEE Standard for Floating-Point Arithmetic [Электронный ресурс]. URL: http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=4610935&filter%3DAND%28p_Publication_Number%3A4610933%29 (дата обращения: 20.03.2015).
- GTX 400 architecture [Электронный ресурс]. URL: http://www.nvidia.com/object/GTX_400_architecture.html (дата обращения: 20.03.2015).
- Программа сибирского отделения РАН «Высокопроизводительные вычисления СО РАН» [Электронный ресурс]. URL: http://icm.krasn.ru/rprojects.php?id=511&scid=516 (дата обращения: 20.03.2015).
- CUDA Toolkit Documentation [Электронный ресурс]. URL: http://docs.nvidia.com/cuda/cuda-c-programming-guide/#axzz3VCinlPKN (дата обращения: 20.03.2015).

