Применение нейронных сетей в качестве регулятора в двухконтурных системах автоматического регулирования



В статье рассмотрен один из методов использования динамических рекуррентных искусственных нейронных сетей (ИНС) для решения прикладных задач оперативной диагностики оборудования, анализа, обучения и работы линейных (классических), гибридных, адаптивных и нечетких алгоритмов автоматического регулирования и управления. Показано, что от компактности и быстродействия работающих по шаговому принципу процессоров промышленных контроллеров зависят перспективы широкого внедрения нейросетевых технологий в промышленности. Приведены примеры использования нейрорегуляторов в двухконтурных системах с объектами с самовыравниванием и без самовыравнивания и сравнение их со стандартными схемами регулирования, такие как каскадная АСР и АСР с дифференциатором. Исследования проводились в приближенных к реальным условиям, а именно с использованием в расчетах исполнительных механизмов и широтно-импульсных модуляторов.

Ключевые слова: искусственная нейронная сеть, синаптические веса, сигнальные графы, матрицы смежности сигнальных графов, шаговый алгоритм, динамическая рекуррентная нейронная сеть, гибридный алгоритм регулирования, эволюционный алгоритм оптимизации многоэкстремальных задач, разностные выражения имитационных моделей линейных динамических звеньев контроллер, параметры объектов управления и регуляторов.

Сейчас в мире идет активное развитие перспективных технологий управления искусственного интеллекта, имитирующих природные процессы, такие как деятельность нейронов мозга. В прикладных задачах все большее распространение находят искусственные нейронные сети (ИНС) [1,2,3,4].

Данное исследование заключалось в изучении искусственной нейронной сети в качестве регулятора для объектов с самовыравниванием и без самовыравнивания и сравнение автоматической системы регулирования (АСР) с ИНС и двухконтурных АСР (каскадная и АСР с дифференциатором).

Для определения возможности практического применения и эффективности обучаемых ИНС были взяты такие модели энергетических объектов, как температура перегретого пара на выходе котла, для регулирования которой обычно применяют схему двухконтурной АСР с дифференциатором, и уровень воды в барабане, регулируемый, как правило по трех-импульсной схеме.

Структурная схема двухконтурной АСР с дифференциатором изображена на рис.1

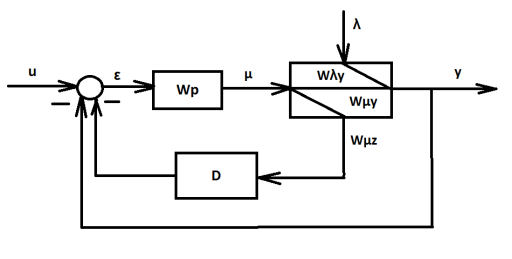
Рис. 1. Двухконтурная АСР с дифференциатором

На вход регулятора, работающего по ПИ-закону, поступает общая ошибка регулирования, равная разнице задания u, регулируемой величины температуры перегретого пара на выходе котла y и опережающего сигнала скорости изменения температуры пара в промежуточной точке dz/dt, рассчитываемой в дифференциаторе.

Передаточные функции объекта по основному и вспомогательному каналу представляют из себя два последовательных апериодических звена и звено транспортного запаздывания, поэтому объект обладает сильным самовыравниванием.

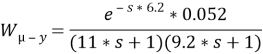(1)

(2)

Структурная схема трех-импульсной АСР уровня воды в барабане котла изображена на рис.2

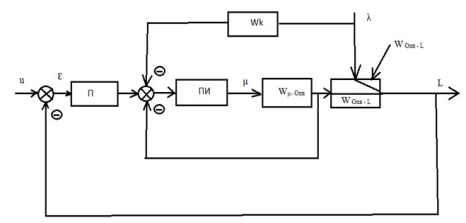
Рис. 2. АСР уровня воды в барабане котла

Расчетная схема регулирования уровня воды в барабане, представляет собой трех-импульсную схему с корректирующим П-регулятором и стабилизирующим ПИ — регулятором. На стабилизирующий регулятор поступает сигнал от малоинерционного канала (передаточная функция W_µ-Gпв(s)), на корректирующий регулятор — сигнал от основного канала, являющегося инерционным (передаточная функция W_Gпв-L(s)). Возмущающим воздействием является расход пара (передаточная функция W_Gпп-L(s)).

Передаточные функции уровня воды в барабане котла по основному каналу и по вспомогательному каналу.

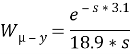(3)

(4)

В автоматической системе регулирования с ИНС необходим всего один нейрорегулятор, на вход которого подаются ошибки по основному и вспомогательному контуру, а на выходе формируется необходимое регулирующее воздействие µ. (Рис.3.)

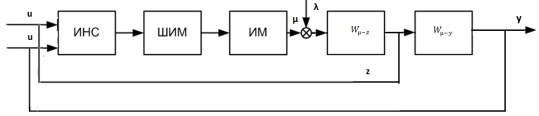
Рис. 3. Структурная схема АСР с нейрорегулятором

В реальных АСР необходимо учитывать влияния исполнительного механизма (ИМ) и широтно-импульсного модулятора (ШИМ) на качество работы АСР. Для приближения характеристики ИМ к идеальной, следует увеличивать его максимальную скорость до бесконечности и сокращать минимальную длительность импульсов ШИМ до нуля.

Однако:

− Для больших скоростей нужен мощный двигатель. Его будет тяжело разогнать, а затем будет наблюдаться значительный выбег.

− Если минимальная длительность импульсов будет мала, то ИМ будет постоянно включаться и выключаться, что приведет к его быстрому износу

− Время полного хода исполнительного механизма Тим указывается в паспорте и нормируется. От значения Тим зависит максимальная скорость исполнительного механизма.

− АСР с обученной нейронной сетью может показать результат приближающийся к идеальному, но если он достигнут резким перемещением исполнительного механизма, то в одну, то в другую сторону (дребезгом) — это технически не реализуемая АСР.

Расчет модели каждого элемента системы и всей АСР проводились с заданным шагом дискретизации. Для широтно-импульсного преобразователя варьировались значения зоны гистерезиса и возврата, для исполнительного механизма — время полного хода. Кроме того, для исключения частого переключения исполнительного механизма на нейрорегулятор была наложена еще одна нелинейная зависимость — зона нечувствительности.

Топология (внутренние связи) ИНС предлагается кодировать сигнальными графами [1,5], а расчет производить матричным методом [1,9].

Для исследования зависимости качества регулирования от топологии сети, были рассмотрены такие ИНС, как прямонаправленная (персептрон), рекуррентная с 1-й, 2-мя и 3-мя обратными связями и полносвязная. Число слоев и нейронов также варьировались.

В ходе эксперимента было установлено, что именно рекуррентная ИНС с одной обратной связью дает наилучшее качество регулирования, а необходимое число нейронов минимально и равно шести. То есть один скрытый слой с тремя нейронами.

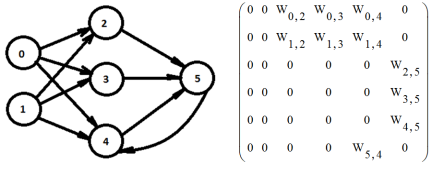
Рис. 4. Структурная схема нейрорегулятора температуры перегретого пара и ее матрица смежности

Для объекта без самовыравнивания обучить рекуррентную ИНС не удалось. Наиболее эффективной топологией сети оказался модифицированный персептрон (Рис.5.), у которого кроме прямых связей от нейронов предыдущего слоя к последующему добавлены сигналы с входных нейронов на выходной. Таким образом формируются дополнительные сигналы ошибки, усиливающие выходное регулирующее воздействие.

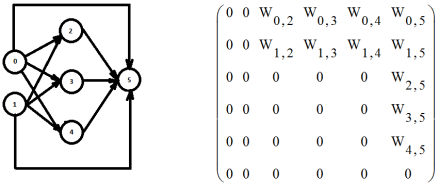
Рис. 5. Структурная схема нейрорегулятора уровня воды в барабане котла и ее матрица смежности

В качестве активационных блоков были испытаны следующие функции:

− Сигмоидальная

− Логарифмическая

− Кусочно-линейная

Наилучших результатов удалось добиться с активационными блоками в виде логарифмической функции, имеющей следующий вид:

(5)

где b — суммарный сигнал на входе нейрона

Инструментом для настройки ИНС в настоящей работе использован вероятностный эволюционный алгоритм оптимизации многоэкстремальных задач. Алгоритм состоит из вероятностной процедуры Монте-Карло для создания множества (популяции) начальных точек для поиска оптимального решения, где Z заданное число, генетической процедуры элиминации (удаления) 10 % неперспективных точек из множества R, операции восполнения множества R новыми, случайно выбранными точками и распределения их регулярным алгоритмом оптимизации по координатам локальных экстремумов. Алгоритм авторская разработка. Его описание опубликовано в [7], а программа зарегистрирована в фонде программ [8].

Параметры нейрорегулятора и регуляторов, используемых в сравнениях, были получены исходя из следующих показателей качества работы автоматической системы регулирования по каждому каналу:

− Модульный интегральный показатель качества

− Степень затухания

− Динамическое отклонение

− Время регулирования

Исходя из вышесказанного можно сделать вывод, что функцией цели для нахождения синаптических весов нейронной сети является модульный интегральный показатель качества. А ограничениями (штрафами, накладываемыми на функции цели) являются все остальные показатели качества.

Тестовый сигнал формировался по каналу возмущения λ (Рис.1-Рис.3).

Далее приведены результаты сравнения работы традиционных АСР с наиболее эффективно обученной АСР с нейрорегулятором.

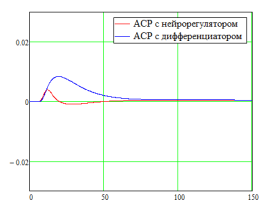
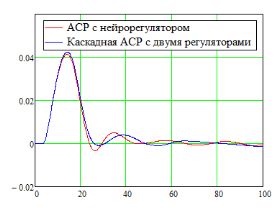
Рис. 6. Выходы объекта с самовыравниванием (а) и объекта без самовыравнивая (б)

На выше приведенных графиках видно, что в первом случае качество работы АСР с нейрорегулятором много лучше, чем АСР с дифференциатором. А во втором случае качество регулирования двух АСР сравнимы друг с другом. Это связано с тем, что в первом случае в структуре ИНС присутствуют обратные связи, которые существенно улучшают качество регулирования.

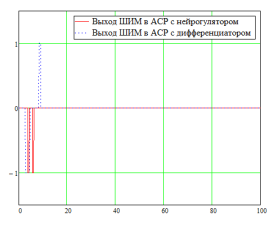
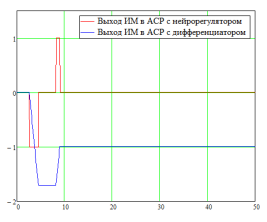
Рис. 7. Выходы технических средств автоматизации в АСР объекта с самовыравниванием

На рис.7 представлены графики выходных сигналов технических средств автоматизации (ТСА), которые соответствуют всем требованиям.

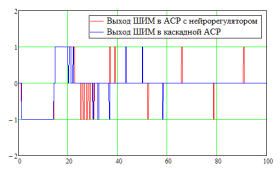
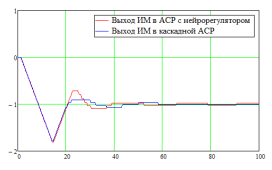
Рис. 8. Выходы технических средств автоматизации в АСР объекта без самовыравнивания

В АСР для объектов без самовыравнивания основным правилом для ТСА является количество импульсов ШИМ, а именно не более 4–6 в минуту после окончания процесса регулирования. Как видно из рис.8 АСР с нейрорегулятором удовлетворяет это условие.

Выводы

1. В работе рассмотрены процессы регулирования АСР объектов с самовыравниванием и без самовыравнивания с учетом влияния технических средств автоматизации на качество регулирования.
2. Нейрорегулятор является перспективным регулятором за счет своей легкости в обучении, более лучшими показателями качества регулирования в сравнении со стандартными АСР используемыми в современном мире.
3. Для повышения качества регулирования следует рассматривать добавление информационных входов искусственной сети и добавление обратных связей в структуре ИНС.
4. Нейрорегулятор в силу своих особенностей может иметь множество входов и выходов. Следует рассматривать перспективу использования ИНС в качестве регулятора сложных многомерных систем.

Литература:

1. Матричный метод расчетов динамических рекуррентных искусственных нейронных сетей Сабанин В. Р., Дементьев Д. А., Казьмирук И. Ю., Репин А. И./ Молодой ученый 2018г. 13 выпуск, часть 1. С. 1–9
2. Ж. Л. Лорьер. Нейронные сети. Системы искусственного интеллекта/ Ж. Л. Лорьер. 1991 год. — 568 с.
3. Автоматические системы регулирования на основе нейросетевых технологий // Сабанин В. Р., Смирнов Н. И., Репин А. И. Сборник трудов конференции Control 2003. МЭИ, 2003. С. 45–51.
4. Управление и инноватика в теплоэнергетике: учебное пособие / А. В. Андрюшин, В. Р. Сабанин, Н. И. Смирнов, — М.: Издательский дом МЭИ, 2011, — 392 с. ил.
5. Некоторые результаты использования искусственных нейронных сетей в качестве регулятора автоматической системы регулирования // Сабанин В. Р., Дементьев Д. А., Казьмирук И. Ю. Сборник трудов 26-й международной научно-технической конференции «Современные технологии в задачах управления, автоматики и обработки информации» г. Алушта, Крым, Россия 14–20 сентября 2017 г. С. 60–61.
6. Харари Френк. Теория графов // Перев. с англ. и предисл. В. П. Козырева. Под ред. Г. П. Гаврилова. Изд. 2-е. — М.: Едиториал УРСС, 2003. — 296 с.
7. Модифицированный генетический алгоритм для задач оптимизации и управления// В. Р. Сабанин, Н. И. Смирнов, А. И. Репин// Exponenta Pro. Математика в приложениях. 2004. № 3–4. С.78–85.
8. Универсальная программа для оптимизации многоэкстремальных задач «Optim-MGA»// В. Р. Сабанин, Н. И. Смирнов, А. И. Репин//Свидетельство об официальной регистрации программы для ЭВМ № 2004610862, 2004 г.
9. Использование метода обратного распространения ошибки для параметрической адаптации шагового нейрорегулятора // Казьмирук И. Ю., Дементьев Д. А., Сабанин В. Р., Архипов А. Б., Кириенок Д. С. // Молодой ученый. — 2018. — № 24. — С. 1–11.