На практике учителя очень часто встречаются такие ситуации, когда обучающиеся не умеют решать квадратные уравнения. Главная задача состоит в том, чтобы научить обучающихся решать квадратные уравнения по первой формуле дискриминанта, а затем вводить и остальные формулы. В результате данного подхода к обучению решения квадратных уравнений большинство обучающихся хорошо запомнят все способы, а первую формулу будут знать все без исключения.
Ключевые слова: квадратные уравнения, дискриминант, теорема Виета, неполные квадратные уравнения, приведенные квадратные уравнения.
In practice, teachers very often encounter situations where students are not able to solve quadratic equations. The main task is to teach students to solve quadratic equations using the first discriminant formula, and then introduce the rest of the formulas. As a result of this approach to learning how to solve quadratic equations, most students will remember all the ways well, and everyone will know the first formula without exception.
Keywords: quadratic equations, discriminant, Vieta theorem, incomplete quadratic equations, reduced quadratic equations.
В настоящее время математическое образование является неотъемлемой частью на всех ступенях общего образования. Без элементарных математических основ невозможно стать образованным человеком.
Тема квадратные уравнения изучается в 8 классе. Обучающиеся должны уметь различать среди всех уравнений квадратные и решать их.
Учитель математики в своей педагогической деятельности часто сталкивается с тем, что обучающиеся не умеют решать квадратные уравнения. А если же они их и решают, то только с помощью первой формулы дискриминанта. Довольно часто можно наблюдать за тем, что обучающийся во время контрольной работы или ответа у доски нерационально решает квадратное уравнение 
c помощью первой формулы дискриминанта, затрачивая на это лишнее время.
Перед учителем стоит главная задача — научить обучающихся решать квадратные уравнения с помощью первой формулы дискриминанта. После того, как каждый обучающийся сможет без затруднений решить квадратное уравнение с помощью данной формулы, имеет смысл введения еще одной формулы, где второй коэффициент четный.
Необходимо донести до обучающихся то, что применение второй формулы более эффективно. Обучающимся во время учебного процесса можно предложить решить квадратное уравнение с большими числами, при условии, что второй коэффициент будет четным числом. Например: 
, 5
. Обучающиеся решают данные квадратные уравнения по первой формуле. В результате чего получают большие числа, и убеждаются в том, что использование данной формулы не совсем целесообразно. После того, как обучающиеся приходят к данному выводу, учитель предлагает формулу, которая позволит облегчить решения данных квадратных уравнений. Один из обучающихся записывает данную формулу на доске: 
.
Далее возникает вопрос, можно ли упростить данное выражение? Обучающиеся с помощью учителя выполняют упрощения:
, где k = 
, получаем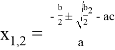 
.
Просим обучающихся сравнить две формулы и найти различия. Далее обучающиеся решают предложенные уравнения с помощью полученной формулы.
Задания нужно отобрать таким образом, чтобы их решать с помощью второй формулы. После того, как большинство обучающихся научаться свободно, применять вторую формулу, имеет смысл вводить ещё одну формулу решения квадратных уравнений — теорема Виета.
Особое внимание при изучении теоремы Виета стоит обратить на то, что существуют различия между прямой и обратной теоремой. В прямой теореме нам дано само квадратное уравнение и его корни, а в обратной теореме только два числа и квадратное уравнение появляется в заключении.
Обучающимся предлагается выполнить задания, в которых необходимо найти сумму и произведение корней квадратного уравнения. Уделить внимание стоит уравнениям, в которых первый коэффициент равен единице. Вводится понятие приведенного квадратного уравнения. Затем предлагается работа, которую можно решить одним из рассмотренных способов. Выбирая первый и второй способ, обучающиеся значительно отстают от тех, которые выбрали третий способ решения квадратных уравнений. Поэтому обучающиеся наглядно убеждаются в рациональном использовании третьего способа.
На следующих уроках обучающиеся вновь буду возвращаться к изучению учебного материала по решению квадратных уравнений. Уравнения отбираются таким образом, чтобы их можно было решить устно, а именно третьим способом, проговаривая каждый шаг вслух. Продолжать стоит до тех пор, пока каждый из обучающихся не научится выполнять с легкостью данное задание.
Повторять все способы решения квадратных уравнений на последующих уроках, предлагая задания на применение всех трех способов. На каждом уроке давать обучающимся самостоятельно решать несколько уравнений выбирая для себя более удобный способ. Проводить данную работу до тех пор, пока обучающиеся в совершенстве не овладеют всеми способами решения квадратных уравнений.
При изучении данной темы рассматриваются и неполные квадратные уравнения. Различные виды неполных квадратных уравнений имеют различные алгоритмы решения. Обучающимся необходимо показать, что общая формула корней применима и для данных случаев.
Тригонометрические, показательные, логарифмические уравнения, уравнения высших степеней сводят к решению квадратных уравнений. Для того чтобы решить неравенства всех типов необходимо разложить квадратный трехчлен на множители, для этого необходимо решить квадратное уравнение.
В результате данного подхода к обучению решения квадратных уравнений большинство обучающихся хорошо запомнят все способы, а первую формулу будут знать все без исключения.
Литература:
- Осколкова В. Г. Дифференцированный подход как залог успешного обучения учащихся математике // Актуальные проблемы теории и методики обучения информатике, математике и экономике. В 2 т. Т. 2: материалы молодежной всероссийской научно — практической конференции. Шадринск: ШГПУ. 2016. С. 210
- Тодарчук В. Г. Применение коллективных и индивидуально — дифференцированных форм обучения при изучении учащимися нового материала // Современное научное общество, образование и наука: материалы научно — практической конференции. Тамбов. 2016
- Мерзляк А. Г. Алгебра: 8 класс: учебник для учащихся общеобразовательных организаций / А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. — М.: Вентана-Граф, 2015. — 256 с.
- Мерзляк А. Г. Алгебра: дидактические материалы: 8 класс: пособие ждя учащихся общеобразовательных организаций / А. Г. Мерзляк, В. Б. Полонский, Е. М. Рабинович и др. — 2-е изд., стереотип. — М.: Вентана-Граф, 2019. — 96 с.: ил. — (Российский учебник)
- 10 способ решения квадратных уравнений [Электронный ресурс]. — Режим доступа: https://nsportal.ru/ap/library/drugoe/2014/08/31/10-sposobov-resheniya-kvadratnykh-uravneniy
