В статье рассмотрены методы перевода чисел из системы остаточных классов в позиционную систему счисления, а также проведен их сравнительный анализ. Показано, что применение классической формы Китайской теоремы об остатках позволяет использовать на 40–75 % меньше операций, чем ее модификации. Однако, модифицированные формы Китайской теоремы об остатках позволяют уменьшить модуль при нахождении остатка числа, что может оказаться более удобным при решении некоторых практических задач.
Ключевые слова: система остаточных классов, позиционная система счисления, Китайская теорема об остатках, обратное преобразование
Одной из наиболее широко используемых непозиционных систем счисления является система остаточных классов (СОК) [1]. СОК может быть эффективно использована в приложениях с преобладающей долей операций сложения, вычитания и умножения, в связи со свойством отсутствия переносов и параллельному выполнению операций [2,3]. Для обратного преобразования числа из СОК в позиционную систему счисления требуется применение Китайской теоремы об остатках (КТО) или ее модификации. Прямое применение КТО приводит к выполнению трудной операции нахождения остатка по большому модулю, что значительно увеличивает время ее выполнения. В данной статье будет рассмотрена не только известная КТО, но и новая (НКТО), которая ускоряет процедуру обратного преобразования, а также будет проведен их сравнительный анализ [4].
Основы системы остаточных классов.
Система остаточных классов (СОК) — непозиционная система счисления, в которой числа представляются в базисе взаимно-простых чисел, называемых модулями ![]() ,
, ![]() , для
, для ![]() . Любое целое число
. Любое целое число 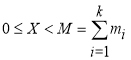 может быть единственным образом представлено в СОК в виде кортежа
может быть единственным образом представлено в СОК в виде кортежа ![]() , где
, где
![]() (1)
(1)
Операции сложения, вычитания и умножения в СОК определяются формулами
![]() ,(2)
,(2)
![]() .(3)
.(3)
Можно выделить два основных преимущества СОК [5]
- Большие числа кодируются в набор небольших остатков, что снижает сложность арифметических операций и упрощает вычислительную систему.
- СОК является непозиционной системой с независимыми арифметическими операциями, таким образом ошибка в одном канале не применяется к другим, а также процессы обнаружения ошибок и их коррекции значительно упрощаются [6].
Тем не менее, такие операции, как обнаружение знака, сравнения, обнаружение переполнения и некоторые другие являются вычислительно сложными в СОК [7].
Методы перевода из системы остаточных классов впозиционную систему счисления
Восстановление числа ![]() по остаткам
по остаткам ![]() основано на Китайской Теореме об Остатках (КТО) [8]
основано на Китайской Теореме об Остатках (КТО) [8]
Теорема 1 (Китайская теорема об остатках) [8]: Пусть ![]() – попарно взаимно простые числа, больше 1, пусть
– попарно взаимно простые числа, больше 1, пусть ![]() Тогда существует единственное неотрицательное решение по модулю P следующей системы сравнений:
Тогда существует единственное неотрицательное решение по модулю P следующей системы сравнений:
![]() (4)
(4)
Следовательно:
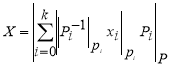 (5)
(5)
где ![]() . Элемент
. Элемент ![]() означает мультипликативный обратный для
означает мультипликативный обратный для ![]() , по модулю
, по модулю ![]() [9].
[9].
Сложность применения теоремы 1 для перевода числа из СОК в позиционную систему заключается в выполнении трудной операции нахождения остатка по большому модулю P.
На рисунке 1 показана схема перевода числа из СОК в ПСС с использованием КТО.
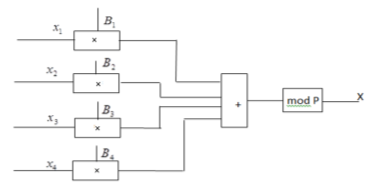
Рис. 1. Схема перевода числа из СОК в ПСС с применением КТО
Матрица
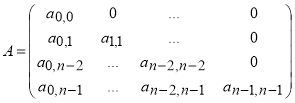 (6)
(6)
характеристическая матрица модулей ![]() , где
, где ![]() . Пусть дано число в СОК
. Пусть дано число в СОК ![]() .
.
Определим вектор:
![]() (7)
(7)
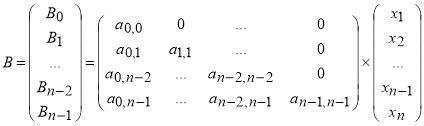 (8)
(8)
Теорема 2 (Новая Китайская теорема об остатках 1) [8]: Пусть дано число в СОК ![]() . Число в десятичной системе счисления может быть вычислено по следующей формуле:
. Число в десятичной системе счисления может быть вычислено по следующей формуле:
![]() (9)
(9)
где ![]() , при любом
, при любом ![]()
Разница между известной КТО и НКТО1 очевидна. Здесь мы используем характеристическую матрицу, состоящую из небольших чисел, вместо больших, как в не модифицированной КТО. Новая КТО представляется в смешанной системе счисления, где коэффициенты — это основания первого порядка. Таким образом, числа которые участвуют в сложении меньше в НКТО1.
На рисунке 2 представлена схема перевода числа из СОК в ПСС с использованием НКТО 1.
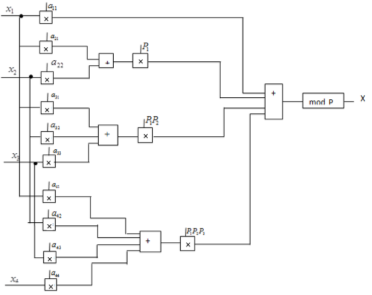
Рис. 2. Схема перевода числа из СОК в ПСС с применением НКТО1
Рассмотрим алгоритм перевода из СОК в позиционную систему счисления (![]() , X).
, X).
a) Если ![]() или
или ![]() :
:
-
Выполним
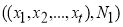 , если
, если 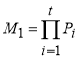 .
.
-
Выполним ((
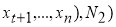 , если
, если 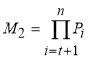 .
.
-
Найдем
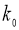 :
: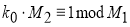
-
Получим:
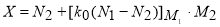 .
.
b) Если ![]() :
:
-
Определим
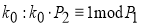 ,
,
-
Получим
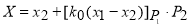 .
.
c) Если n=1:
Теорема 3 (Новая Китайская теорема об остатках 2) [8]: Рассмотренный алгоритм корректно восстанавливает число ![]() по остаткам
по остаткам ![]() .
.
Отличие НКТО2 от известной КТО очевидно, ведь здесь, как и в случае с НКТО1 отсутствует вычислительно сложная операция по большому модулю.
На рисунке 3 схематически представлен процесс перевода числа из СОК в ПСС с использованием НКТО 2.
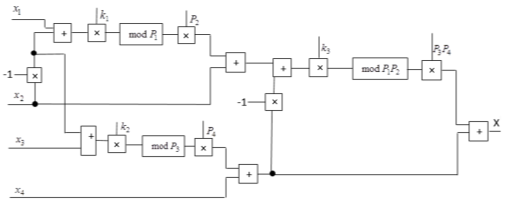
Рис. 3. Схема перевода числа из СОК в ПСС с применением НКТО 2
Пример. Осуществим процедуру перевода числа ![]() по модулям (2,3,5,7) из СОК в ПСС. С использованием известной КТО получим:
по модулям (2,3,5,7) из СОК в ПСС. С использованием известной КТО получим:
![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, 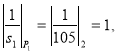
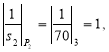
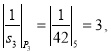
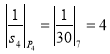
![]()
С использованием НКТО1 имеем:![]()
![]()
![]()
Составим характеристическую матрицу:
![]()
![]()
![]()
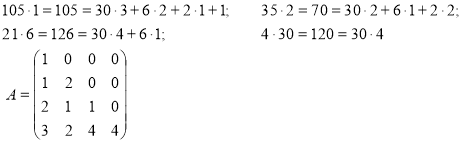
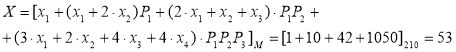
С использованием НКТО2:
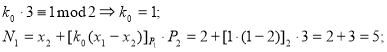
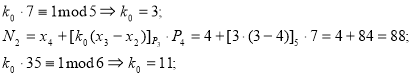
![]() .
.
Таблица 1
Сравнительный анализ методов перевода числа из СОК вПСС
|
Метод |
Используемые блоки |
Наибольший путь | ||||
|
Сложение |
Умножение |
Взятие по модулю |
Сложение |
Умножение |
Взятие по модулю | |
|
КТО |
1 |
4 |
1 |
1 |
1 |
1 |
|
НКТО1 |
4 |
13 |
1 |
2 |
2 |
1 |
|
НКТО2 |
6 |
8 |
3 |
4 |
6 |
2 |
Из таблицы 1 видно, что для перевода числа из СОК в ПСС, применяя известную КТО, понадобится 1 блок сложения, 4 блока умножения и 1 блок взятия числа по модулю, при этом наибольший путь равен 3 (по 1 блоку на каждую операцию). Если использовать НКТО1, то понадобится 4 блока сложения, 13 блоков умножения и 1 блок взятия числа по модулю, при этом наибольший путь равен 5 (по 2 блока сложения и умножения и 1 блок взятия по модулю). Если применять НКТО2 данная операция займет 6 блоков сложения, 8 блоков умножения и 3 блока взятия по модулю, и тогда наибольший путь будет равен 12 (4 блока сложения, 6 блоков умножения и 2 блока взятия по модулю). Из таблицы видно, что наименьшее количество блоков понадобится, если использовать ранее известную КТО.
Заключение.
Результаты исследования показали, что наиболее рациональным является применение известной КТО, так как ее реализация требует использования наименьшего количества блоков с операциями. КТО требует на 40 % меньше операций в наибольшем пути, по сравнению с НКТО1, и на 75 % меньше операций в наибольшем пути, по сравнению с НКТО2.
С другой стороны, для решения некоторых задач может оказаться удобнее использовать НКТО1 и НКТО2, так как они исключают громоздкие вычисления по большому модулю.
Литература:
- Червяков Н. И., Велигоша А. В., Калмыков И. А., Иванов П. Е. Цифровые фильтры в системе остаточных классов // Радиоэлектроника. — 1995. Т. 38, № 8. — С. 11–20.
- Червяков Н. И., Евдокимов А. А., Головко А. Н. Гибридная нейронная сеть для коррекции ошибок «на лету» в системе остаточных классов // Нейрокомпьютеры: разработка, применение. — 2009, № 10. — С. 13–20.
- Cardarilli G. C., A. Nannarelli A., Re M. «Residue number system for low-power DSP applications», Proc. 41st Asilomar Conf. Signals, Syst., Comput., 2007. pp. 1412–1416.
- Chervyakov N. I., Lyakhov P. A., M. G. Babenko M. G. Digital filtering of images in a residue number system using finite-field wavelets, Automatic Control and Computer Sciences 48 (3), 2014. pp. 180–189.
- Peemen M., Setio A. A. A., Mesman B and Corporaal H. Memorycentric accelerator design for convolutional neural networks, 31st International Conference on Computer Design (ICCD2013), 2013, pp. 13–19.
- Farabet C., Martini B., Akselrod P., Talay S., LeCun Y and Culurciello E. Hardware accelerated convolutional neural networks for synthetic vision systems, Int’l Symp. on Circuits and Systems (ISCAS2010), 2010, pp. 257–260.
- Chervyakov N. I., Molahosseini A. S., Lyakhov P. A., Babenko M. G., Deryabin M. A.: «Residue-to-Binary Conversion for General Moduli Sets Based on Approximate Chinese Remainder Theorem», International Journal of Computer Mathematics, 2016, pp. 1–17.
- Parhami B. Computer Arithmetic: Algorithms and Hardware Designs/ B. Parhami, Oxford University Press, Inc., 2000. – 492 p.
[1] Работа выполнена при поддержке гранта Президента Российской Федерации МК-5980.2016.9.

