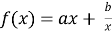В статье систематизированы сведения о функции
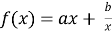
Ключевые слова : функция, экстремум функции, асимптота, физическая задача, неравенство Коши.
Для полного исследования и понимания свойств функции
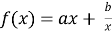
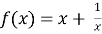
Функция f(x) определена при всех действительных х, кроме х=0, и является непрерывной на каждом из промежутков ( - ; 0) и (0; +).
Функция f(x) является нечетной, так как ее область определения симметрична относительно нуля и для каждого х из области определения выполняется равенство:
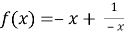
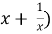
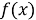
График функции не пересекает координатные оси Ох и Оу, так как уравнение
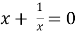
Видим, что
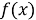
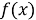
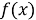
Видно также, что
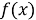
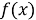
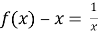
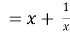



Функция
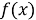
f (x)
= 1 -
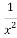
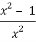
Критические точки функции находим из уравнения f (x) = 0. Уравнение
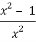
Точки -1, 0, 1 развивает числовую ось на четыре промежутка:
(-; -1), (-1; 0), (0, 1), (1; +).
Неравенство
f (x)
0, то есть
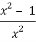
Следовательно, функция
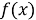
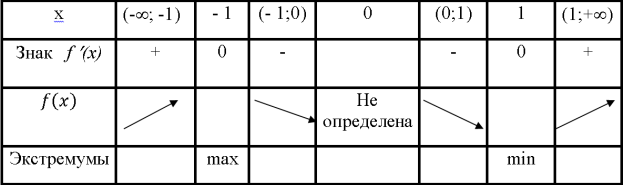
Пользуясь нечетностью функции, построим весь график (рис.1).
Рис.1
Рассмотрим теперь пример из математики, при анализе которого используются основные свойства функции
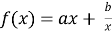
Пример 1. Найдите пары чисел (х; у),удовлетворяющие уравнению:
22 –
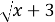
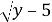
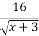
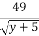
Анализ: Запишем исходное уравнение виде:
(
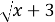
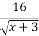
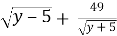
Воспользуемся доказанным ранее неравенством для
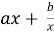
Тогда
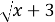
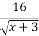
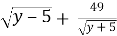
Следовательно: (
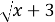
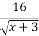
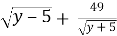
Поэтому уравнение (1) равносильно системе
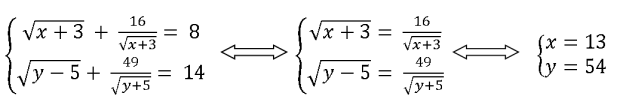
Рассмотрим пути применения функции
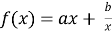
Пример 2. Поезд начинает двигаться с постоянным ускорением а вдоль прямолинейного участка пути. На расстоянии l от последнего вагона на перпендикуляре к направлению движения поезда находится пассажир. С какой минимальной скоростью может бежать пассажир, чтобы догнать поезд? В каком направлении он должен бежать в этом случае? Движение пассажира считать равномерным.
Анализ. Пусть встреча пассажира с последним вагоном произошла в точке В (рис.2). Треугольник АВС прямоугольный. Тогда, используя теорему Пифагора, можно записать
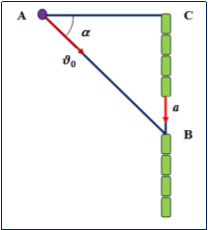
Рис.2
BC2 = AB2 – l2,
или,
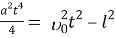
Отсюда выразим квадрат начальной скорости:
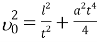
Для того чтобы скорость υ
0
была минимальной, необходимо, чтобы сумма
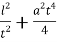
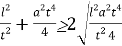
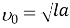
Обратим внимание на то, что минимальная скорость достигается при условии
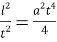
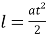
Значит, СВ=
l
, т.е. треугольник ACВ — равнобедренный, и =45. Получили, что пассажиру следует бежать под углом 45 к АС со скоростью
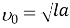
Литература:
-
Бардушкин В.В., Прокофьев А.А. Функция
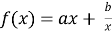
-
Мукушев Б.А. Функция