Использование среды GeoGebra при решении задач с параметрами



GeoGebra — это программная среда, объединившая в себе важные математические представления: табличное, алгебраическое и геометрическое. Она имеет динамическую структуру и позволяет создавать различные конструкции для решения задач, в том числе с параметром.

В данной статье рассмотрим решение задания с параметром графическим способом, используя программную среду GeoGebra.

Задача:

Найти все значения параметра a, при каждом из которых система:

не имеет решений.

Решение:

В первом неравенстве дано произведение двух выражений. Первое из них описывает окружность с центром в точке (3;3) и радиусом 1, а второе — точку (1;0). Т. к. само неравенство меньше нуля, то его решением будет объединение внутренней части окружности и точки. Уравнение в системе — это семейство прямых: . Для того, чтобы данная система не имела решений необходимо отсутствие пересечения прямой с окружностью, а также прохождения через точку.

Выполним построения в компьютерной среде GeoGebra и найдем значения параметра, при которых данная ситуация будет выполняться.

1. Запустим программу GeoGebra. Появится окно, похожее на графический редактор.

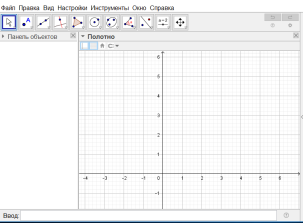
Рис. 1. Интерфейс программы GeoGebra

2. Строим объекты для неравенства. Для этого в строке ввода делаем запись: 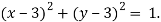Можно записать и неравенством, тогда будет выделена и внутренняя область окружности. Определим центр данной окружности. Для этого вводим команду: центр(“conic”), где вместо объекта прописываем букву, которой будет назван построенный объект в панели объектов. Точно также строим точку, для которой задано уравнение: .

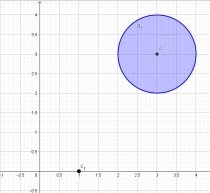
Рис. 2. Результат второго шага решения

3. Построим теперь график функции с параметром. Для этого находим в панели инструментов «ползунок» и создаем его на полотне. Название параметра оставим a, шаг для начала выберем 0,5. Далее вводим в строку ввода 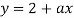. Чтобы было удобно передвигать ползунок при помощи клавиатуры, выделим его правой клавишей мыши и дальнейшее изменение параметра будет управляться стрелками.

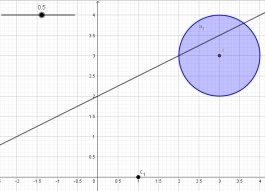
Рис. 3. Результат третьего шага решения

4. Первые точки, которые нам нужны — это точки касания прямой с окружностью. Т. к. мы пока не знаем устроит ли нас выбранный шаг для параметра, попробуем поискать получается ли точка пересечения с одной или с другой стороны окружности. Точка появится при параметре равном 0. Отметим полученную точку пересечения, используя инструмент «точка пересечения».

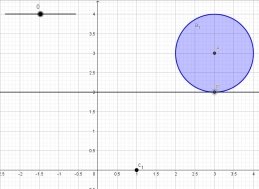
Рис. 4. Результат четвертого шага решения

5. Для поиска второй точки, создадим еще один ползунок, уменьшив шаг до 0,1. При этом прямая будет строиться заново, т. к. ползунок имеет уже другое имя. Т. е. повторим этап построения прямой, заменив в уравнении букву параметра. Чтобы не путаться с именами ползунков, можно в свойствах объекта поставить — показывать только значение. Определим вторую точку касания, она появится при значении — 0,75. Т. е., получаем, что значения между 0 и 0,75=3/4 необходимо исключить, т. к. в этом случае прямая пересекает окружность.

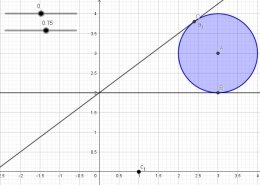
Рис. 5. Результат пятого шага решения

6. Осталось найти значение параметра, при котором прямая будет проходить через точку (1;0). Создадим еще один ползунок и снова построим прямую. Приблизим её к точке пересечения. Для того, чтобы увидеть попадает ли прямая в точку пересечения, выполним пересечение прямой с осью Ox чуть раньше и будем изменять значение параметра пока значение точки не станет (1;0).

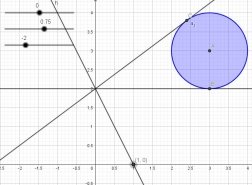
Рис. 6. Результат шестого шага решения

7. Для того, чтобы показать, что все значения параметра между найденными будут являться решением задачи — создадим еще один ползунок. Введём уравнение прямой и сделаем анимацию данного объекта. Для этого выберем в свойствах объекта «анимировать». Скорость движения можно изменять при необходимости.

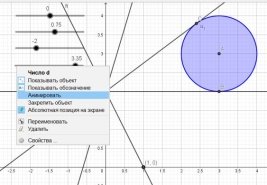
Рис. 7. Результат седьмого шага решения

8. Ответ: .

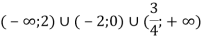Таким образом, компьютерная среда GeoGebra позволяет более наглядно

представить графический способ решения различных заданий с параметром и возможно упростить работу с задачами данного типа.

Литература:

1. Зиатдинов Р. А. О возможностях использования интерактивной геометрической среды GeoGebra 3.0 в учебном процессе // Материалы 10-й Международной конференции «Системы компьютерной математики и их приложения» (СКМП-2009), СмолГУ, г. Смоленск, 2009, C. 39–40.

2. http://teachersclub.ru/uncategorized/geogebra.html / Электронный ресурс. Клуб учителей. ЛОГОС. GEOGEBRA.

3. https://ege.sdamgia.ru/problem?id=516336 / Решу ЕГЭ. Образовательный портал для подготовки к экзаменам (Математика).