Введение. В математической физике дифференциальные уравнения используются для описания многих физических явлений. Решения этих уравнений часто не выражаются элементарными функциями, поэтому вводится класс функций, называемых специальными функциями. Специальные функции широко используются в различных областях математической физики, таких как квантовая механика, электродинамика, теплопроводность и гидродинамика. В этой статье мы больше сосредоточимся на их роли в квантовой механике и оптике, а также объясним на конкретных примерах.

Основные виды и применение специальных функций:

1. Гамма-функция (Γ (z)):

Определение: , где .

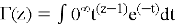
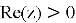
Свойства:

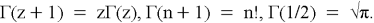
Применение: используется в теории вероятностей, статистике, комбинаторике и физике при вычислении различных интегралов. Гамма-функция часто встречается при нормировании амплитуд вероятности в квантовой теории.

Пример: в квантовой механике Гамма-функция используется для определения константы нормализации при описании гауссовского пакета (Gaussian wave packet). [4.с.39]

2. Функции ):

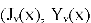
Определение: решения уравнения Бесселя:

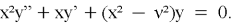
Свойства: рекуррентные отношения, асимптотические выражения, свойства ортогональности.

Использование:

Оптика: в описании дифракции света, проходящего через круглую щель (диск Эйри). Также используется при изучении распространения электромагнитных волн в оптических волокнах. Функции Бесселя играют важную роль в определении разрешающей способности оптических систем.

Пример: интенсивность света, проходящего через круглое отверстие диаметром a(Airy disk): , где - функция Бесселя первого порядка, — волновое число, — угол.

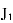
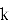
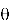
Квантовая механика: при описании движения частиц в сферически симметричном потенциале, особенно для частицы в потенциальной яме на трехмерной бесконечной глубине.

Путь решения: решая уравнение Шредингера дробно в сферических координатах, радиальная часть выражается функциями Бесселя. [1.с.125]

3. Полиномы Лежандра ):

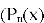
Определение: решения уравнения Лежандра::

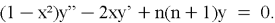
Свойства: свойства ортогональности, рекуррентные отношения, Формула Родригеса.

Использование: Квантовая механика: в описании угловой части при решении уравнения Шредингера атома водорода, а также в качестве собственных функций оператора углового момента. Используется в молекулярной физике для описания вращательного движения молекул.

Например: для состояния, в котором квантовое число углового момента , угловая часть (spherical harmonics) , где является Полином Лежандра первого порядка. [2.с.74]

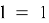
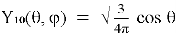
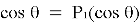
Путь решения: вы можете определить полиномы Лежандра, разобрав уравнение Шредингера и установив соответствующие граничные условия.

Электростатика: аппроксимирует потенциал точечного заряда за счет многоатомного расширения. Также используется при моделировании геопотенциала земли.

Пример: дипольный потенциал:

, где дипольный момент, угол, — расстояние.

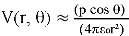
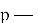
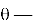
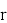
4. Полиномы Эрмита ):

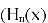
Определение: решения уравнения Эрмита: .

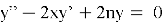
Свойства: свойства ортогональности, рекуррентные отношения, генерирующая функция.

Использование:

Квантовая механика: в описании квантовых состояний гармонического осциллятора, как решения уравнения Шредингера. Используется в квантовой теории поля при описании мод бозонов.

Например: волновая функция основного состояния гармонического осциллятора: ), где константа перед экспонентой связана с полином Эрмита. [6, с. 95]

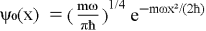
Путь решения: вы можете определить энергетические уровни и волновые функции, решив уравнение Шредингера с помощью полиномов Эрмита.

Оптика: в описании мод гауссовских лучей. Поперечное сечение постоянных лучей в лазерах характеризуется Эрмитово-Гауссовскими функциями.

Пример: интенсивность излучения Эрмита-Гаусса: , где — радиус луча, и - полиномы Эрмита.

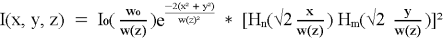
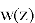
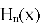
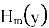
5. Полиномы Лагерра ):

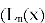
Определение: решения уравнения Лагерра:

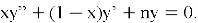
Свойства: свойства ортогональности, рекуррентные отношения, генерирующая функция.

Использование:

Квантовая механика: при описании радиальной части при решении уравнения Шредингера атома водорода.

Например: волновая функция атома водорода , где связан с полиномом Лагерра, — радиус бора.

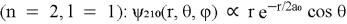
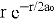
Путь решения: вы можете определить полиномы Лагерра, разобрав уравнение Шредингера и установив соответствующие граничные условия. [7, с. 87]

Оптика: в описании мод лучей Лагерра-Гаусса. Эти лучи используются в оптических устройствах для улавливания частиц (оптический пинцет) и передачи информации.

Вывод. Специальные функции являются неотъемлемой частью математической физики и играют важную роль в решении физических задач. Их использование в квантовой механике и оптике подчеркивает их практическое значение. Глубокое понимание их свойств и областей применения позволяет моделировать и анализировать физические явления. В данной статье рассмотрены основные виды специальных функций и примеры их применения в квантовой механике и оптике, а также показаны пути решения конкретных задач. Проведение более глубоких исследований по этой теме позволит полностью понять важность специальных функций в математической физике.

Литература:

1. Арфкен, Г. Б. Математические методы для физиков / Г. Б. Арфкен, Х. Вебер. — М.: Бином, 2001. — 1024 с. — Текст: непосредственный.
2. Снитко, В. А. Специальные функции и их применение в физике / В. А. Снитко. — М.: МГУ, 2007. — 248 с. — Текст: непосредственный.
3. Полянский, А. А. Специальные функции в физике / А. А. Полянский. — М.: Лань, 2019. — 320 с. — Текст: непосредственный.
4. Байкулов, К. А. методы математической физики / К. А. Байкулов, А. Ж. Нуртаев. — Алматы: КазНУ, 2010. — 356 с. — Текст: непосредственный.
5. Lebedev, N. N. Special Functions and Their Applications / N. N. Lebedev. —: Dover Publications, 1972. — Текст: непосредственный.
6. Olver, F W J NIST Handbook of Mathematical Functions / F W J Olver. — Cambridge: Cambridge University Press, 2010. — Текст: непосредственный.
7. Morse, P. M. Methods of Theoretical Physics, Vol. I & II / P. M. Morse, H. Feshbach. —: McGraw-Hill, 1953. — Текст: непосредственный.