Преобразование Фурье стало мощным инструментом, применяемым в различных научных областях. В некоторых случаях его можно использовать как средство решения сложных уравнений, описывающих динамические процессы, которые возникают под воздействием электрической, тепловой или световой энергии. В других случаях оно позволяет выделять регулярные составляющие в сложном колебательном сигнале, благодаря чему можно правильно интерпретировать экспериментальные наблюдения в астрономии, медицине и химии.
В данной статье решаем смешанную задачу для гиперболической системы с помощью преобразование Фурье. Гиперболические системы описывают колебательные процессы, распространение звуковых волн.
В области ![]() рассмотрим следующую задачу [3]:
рассмотрим следующую задачу [3]:
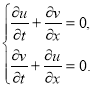
![]() (1)
(1)
![]() (2)
(2)
Для решения этой задачи используем преобразование Фурье.
Преобразование Фурье для функции двух переменных имеет следующий вид [1]:
![]() (3)
(3)
![]() (
(![]() )
)
Для нашей задачи верны следующие равенства:
![]() (4)
(4)
![]() (
(![]() )
)
Чтобы применить преобразование Фурье к задаче, уравнения системы (1) умножая на ![]() интегрируем по области R и получаем следующее:
интегрируем по области R и получаем следующее:
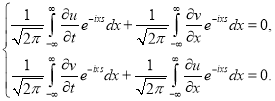
Для нашей задачи верны следующие вычисления:
![]()
![]()
![]()
![]()
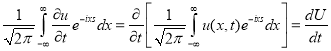
![]()
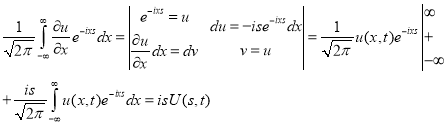
Точно так же
![]()
Тогда задача (1), (2) принимает следующий вид:
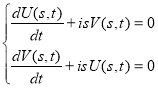 (5)
(5)
![]()
![]()
Из системы (5) получаем задачу Коши для функции ![]() :
:
![]() (6)
(6)
![]()
![]() (7)
(7)
здесь ![]() .
.
(6), (7) — задача Коши для дифференциального уравнение второго порядка, находим её решение:
![]() (8)
(8)
Теперь, чтобы найти решение заданной задачи, для функции (8) применяем (![]() );
);
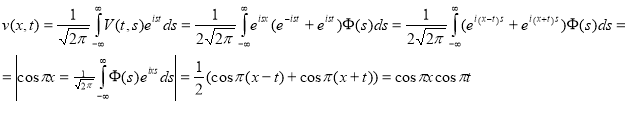
Значит, ![]()
Теперь, воспользовавшись равенством ![]() получаем:
получаем:
![]() (9)
(9)
Для функции (9) применяем (4), находим ![]() .
.
Тогда решение поставленной задачи имеет следующий вид:
![]()
Двойную спираль ДНК, циклы солнечной активности и сложные электронные сигналы математически можно представить в виде ряда волнообразных кривых. Эта идея лежит в основе мощного аналитического инструмента, название которого преобразование Фурье.
Преобразование Фурье вычисляется всякий раз, когда мы слышим звук. Ухо автоматически выполняет вычисление, проделать которое наш сознательный ум способен лишь после нескольких лет обучения математике. Мозг превращает эту информацию в воспринимаемый звук.
Аналогичные операции можно производить с помощью математических методов над звуковыми волнами или практически над любыми другими колебательными процессами — от световых волн и океанских приливов до циклов солнечной активности. Пользуясь этими математическими приёмами, можно раскладывать функции, представляя колебательные процессы в виде набора синусоидальных составляющих — волнообразных кривых, переходящих от максимума к минимуму, затем опять к максимуму, подобно океанской волне. Преобразование Фурье — это функция, описывающая амплитуду и фазу каждой синусоиды, соответствующей определённой частоте. (Амплитуда представляет высоту кривой, а фаза — начальную точку синусоиды.)
Точно также, как преобразования Фурье и гиперболические системы, имеют широкое применение в математике, в физике и в других сферах науки. Задачи, поставленные дифференциальным уравнениям высшего порядка с частными производными, приводятся к задачам, поставленным гиперболической системы первого порядка. Решение смешанных задач для гиперболических систем при помощи преобразование Фурье более удобный метод решение, потому что они приводятся к решению задач для обыкновенных дифференциальных уравнений.
Литература:
- М. Салоҳиддинов. Математик физика тенгламалари. Т. “Ўз-н” 2002, 445стр.
- Годунов С. К. Уравнения математической физики. М. «Наука» 1967.
- С. К. Годунов, Е. В. Золотарева. Сборник задач по уравнения математической физики. Н. 1987г, 96стр.

