Техника приближенных вычислений при решении инженерных и экономических задач



В статье рассмотрены вопросы формирования навыков приближенных вычислений в практике решения инженерных и экономических задач. На основе известных приемов устного счета сформулирован набор правил быстрого выполнения различных математических операций, включая вычисление тригонометрических функций и логарифмирование. Предложенная методика наиболее востребована в инженерной практике и экономике, где фактор времени принятия решения зачастую первичен по отношению к степени точности математического обоснования.

Ключевые слова : устный счет, четырехзначная арифметика, приближенные вычисления, погрешность, линейная интерполяция, тригонометрические функции, логарифмирование.

Вычислительная техника проникла практически во все области человеческой деятельности, коренным образом изменив характер труда специалистов. Логарифмические линейки и арифмометры канули в небытие, а вмести с ними уходят в прошлое и навыки ручных вычислений, которые ранее прочно формировались в школах и университетах. Так, например, 68 % работодателей при привлечении молодых специалистов в штат, считают наиболее важным способность понимать и работать с числами [3, с.96]. Одним из критериев приема на работу является вопрос, насколько хорошо будущий сотрудник умеет считать и умеет ли вообще? Примечательно, что британские исследователи [7, с.7] отмечают прямую связь вычислительных навыков молодых специалистов со способностью анализировать и принимать решения — это подтвердили 68 % опрошенных работодателей.

Несмотря на очевидную актуальность, публикаций по данной теме сравнительно мало. Большинство пособий, например, [1, 2], ориентированы на развитие приемов устного счета у детей школьного возраста. Другие пособия [4–6] ориентированы на более широкий круг читателей, разных по возрасту и профессиональной деятельности. Эти работы содержат объемный свод правил устного счета, написаны в докомпьютерный период и почти не затрагивают специфику приближенных вычислений. На практике этими навыками владеют либо преподаватели математики, либо отдельные любители устных вычислений.

Цель работы — создать набор правил, позволяющих устно, либо вручную, без калькулятора быстро производить приближенные вычисления различной сложности (арифметические, тригонометрические, логарифмирование). Именно такая техника приближенных вычислений наиболее востребована в практике инженерной деятельности, неразрывно связанной в условиях рыночных отношений с задачами экономического характера.

В основу положена гипотеза о том, что четырехзначная целочисленная арифметика и навыки линейной интерполяции могут служить основой широкого спектра приближенных вычислений с вещественными числами с точностью порядка одного процента.

Четырехзначная арифметика. В инженерной практике и экономических расчетах не требуется высокой точности вычислений. Обычно бывает достаточно двух-трех верных знаков. Однако, чтобы их получить, нужно хорошо владеть устными приемами целочисленного умножения и возведения в степень в 4-значном диапазоне. Вычисления производятся с помощью следующих формул сокращенного умножения:

а) для произведения одинаковых чисел (возведение в квадрат):

a ² = ( a + c ) ∙ ( a - c ) + c ²

б) для произведения разных чисел:

a∙b = (a+c)∙b — c∙b

a∙b = (a-c)∙b + c∙b

Число с выбирается таким образом, чтобы полученная сумма ( a + c ) или разность ( a - c ) было числом, удобным для выполнения устных операций.

Рассмотрим несколько примеров:

Возведение в квадрат 2-значных чисел. Выбираем удобное число, затем вычисляем результат по формуле сокращенного умножения:

19 ² = (19–1) ∙ (19 + 1) + 1 ² = 18 ∙ 20 + 1 = 360 + 1 = 361

89 ² = 100 ∙ (89–11) + 11 ² = 100 ∙ 89 + 121 = 8900 + 121 = 9021

Умножение 2-значного числа на 1-значный множитель. Перемножаем десятки, затем прибавляем (или отнимаем) произведение единиц:

21 ∙ 3 = (21–1) ∙ 3 + 1 ∙ 3 = 20 ∙ 3 + 1 ∙ 3 = 60 + 3 = 63

78 ∙ 7 = 80 ∙ 7–2 ∙ 7 = 560–14 = 546

Умножение 3-значного числа на 1-значный множитель.

788 ∙ 6 = 800 ∙ 6–12 ∙ 6 = 4800 + 72 = 4872

Произведение 2-значных чисел.

19 ∙ 76 = 20 ∙ 76–1 ∙ 76 = 1520–76 = 1444

32 ∙ 97 = 100 ∙ 32–3 ∙ 32 = 3200–96 = 3104

Реже возникает необходимость возведения в куб и в 4-ю степень.

Возведение в куб (через возведение в квадрат и перемножение):

21 ³ = 21 ∙ 441 = 20 ∙ 441 + 441 = 8820 + 441 = 9261

Возведение в 4-ю степень (через двойное возведение в квадрат):

7 ⁴ = 49 ² = 50 ∙ 48 + 1 ² = 2400 + 1 = 2401

Можно использовать и иные приемы целочисленной арифметики [5, 6], если уже сложились навыки их успешного применения.

Вещественные числа и погрешности. При выполнении арифметических операций с вещественными числами перед вычислителем стоит задача нормировки , то есть приведения сомножителей к форме натуральных чисел, дающих результат до четырех значащих цифр.

При нормировке сомножителей, следует определить и записать (запомнить) на сколько позиций вправо (+) или влево (-) необходимо перенести десятичную запятую в конечном результате:

76 ∙ 0,041 = 10 ^–3 ∙ (76∙41 = 40 ∙76 + 1∙76 = 3040+76 = 3116) = 10 ^–3 ∙ 3116 = 3,116

380 ² = 10 ⁺² ∙ (38 ² = 40 ∙ 36 + 4 = 1440 + 4 = 1444) = 10 ⁺² ∙ 1444 = 144400.

Исходные значения могут содержать три и более значащих цифры. В этом случае при проведении нормировки «лишние» значащие цифры следует отбросить, минимизируя , по возможности, погрешность вычислений.

Минимизация погрешности достигается за счет округления одного или двух сомножителей, причем два сомножителя лучше округлять вразные стороны . Дополнительно можно снизить погрешность учетом остатка за счет отброшенной части. Здесь и далее в конце строки после косой черты «/» будем показывать относительную погрешность результата в процентах.

Округление одного сомножителя :

0,00742∙1,8 ≈ 10 ^–5 ∙ (74∙18= 20 ∙74–2∙74=1480–148=1332) ≈ 0,01332 /-0,27 %

3,141593 ∙ 5,46 ≈ 10 ^–2 ∙ ( 3 ∙546 = 1638) ≈ 16,38 / -4,51 %

Округление двух сомножителей в разные стороны :

125 ² ≈ 10 ⁺² ∙ (12∙13 = 10 ∙13 + 2∙13 = 130 + 26 = 156) ≈ 15600 /-0,16 %

3,141593 ∙ 5,46 ≈ 10 ^–2 ∙(31∙55= 60 ∙31–5∙31=1860–155=1705) ≈ 17,05 /-0,60 %

Округление с добавлением остатка, т. е. с корректировкой итогового значения путем добавления произведения отброшенной части на второй сомножитель:

0,00742 ∙ 1,8 ≈ 10 ^–5 ∙ (74∙18= 20 ∙74–2∙74=1480–148=1332) ≈ 0,013 36 /+0,03 %

3,141593 ∙ 5,46 ≈ 10 ^–2 ∙ ( 3 ∙546 = 1638) ≈ 17, 18 /+0,16 %

Здесь приближенные результаты 0,01332 и 16,38 скорректированы соответственно на величины 0,0004 (0,00002∙1,8) и 0,8 (0,141593∙5,46).

В последнем примере вычисления длины окружности диаметром 5,46 (3,141593∙5,46) показано, как правильно выбранный способ округления снизил погрешность вычисления с 4,51 % до 0,16 %. Заметим, что и без вычислений видно, что отбрасывание остатка 0,141593∙5,46 повышает погрешность. В качестве приближенного ответа можно было бы сразу записать значение 17,2.

Задача 1 . Вычислить объем накопительного бункера цилиндрической формы диаметром 4,8 м с коническим днищем (см. рис. 1).

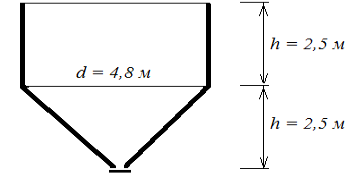
Рис. 1. Бункер для сыпучих материалов

Решение . Из курса геометрии известно, что при равной высоте h объем конуса в 3 раза меньше объема цилиндра:

V = V _ц + V _к = 4/3 ∙ π d ² h /4 = π/3 ∙ d ² h = 3,14/3 ∙ 4,8 ² ∙2,5 ≈ 1,05∙5,76∙2,5 ≈ 60 м ³ .

Интерполяция при обратных операциях. Ранее мы рассмотрели прямые операции умножения и возведения в степень. Приближенность таких вычислений заключалась лишь в отбрасывании «лишних» знаков с целью применения навыков целочисленных вычислений. Иное дело — обратные операции: деление и извлечение корня.

Для поиска результата от деления или извлечения корня сокращение числителя и знаменателя на общий множитель, равно как и вынос общего числа за знак радикала, как правило не сильно упрощает поиск ответа. Гораздо эффективнее оказывается поиск ближайших граничных значений с последующей интерполяцией между ними (см. рис. 2), формула которой вытекает из условия подобия треугольников.

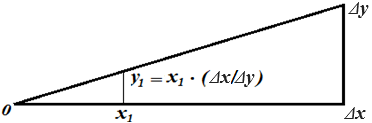
Рис. 2. Схема линейной интерполяции

Используя приемы устного умножения и возведения в степень, найдем интервал, внутри которого находится искомый результат. Следует стремиться к тому, чтобы целочисленные значения границ интервала отличались друг от друга на одну единицу. Это упростит вычисления по формуле интерполяции (см.рис.1 при Δ y =1). Затем проинтерполируем в пределах этого интервала и найдем приближенное значение результата деления или извлечения корня.

Взятый за основу принцип четырехзначной арифметики позволяет пренебречь влиянием нелинейности обратных функций и извлечения корней вследствие незначительности вносимой погрешности (см. рис.3).

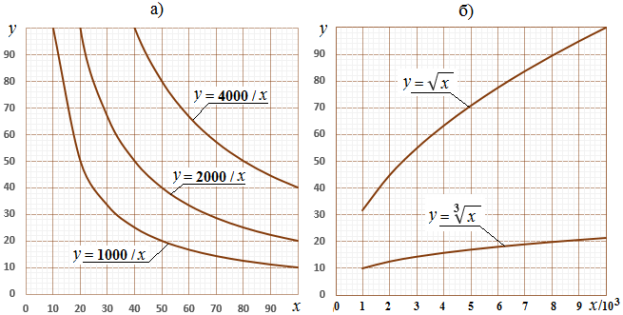
Рис. 3. Графики функций в 4-значном диапазоне: а) гипербола вида k / x ; б) извлечение корня

Рассмотрим несколько приемов деления и извлечения корней.

Деление четырехзначного числа на двухзначное . Например, 3749 / 76.

Последовательным устным перемножением находим такое граничное число 50 (соответствующее делимому 50 ∙76 = 3800), при изменении которого на одну единицу ( 49 ∙76 = 3800–76 = 3724) исходное делимое попадает в данный интервал (3800 > 3749 > 3724). Искомое частное 50–25∙1/76 ≈ 49,3 /-0,06 %

Обратно пропорциональная функция вида 1/х. Найти значение 1 / 76.

Выполняем нормировку: 1/76 = 10 ^–3 ∙ 1000/76. Первое граничное число 14 (14∙76=1064). Второе граничное число 13 (1064–76=988). Тогда искомое частное 1/76 ≈ 10 ^–3 ∙ 13+12/76 ≈ 0,0132 / +0,32 %

Вычисление квадратного корня. Например, корень из 4432:

Пусть первый граничный корень равен 65, тогда 65 ² = 4225. Наугад — второй граничный корень 67, тогда 67 ² = 4489. Диапазон подкоренных значений: 4225<4432<4489, => ≈ 67–57∙2/264 ≈ 66,5 / -0,11 %

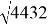
Вычисление кубического корня. Например, из 0,714:

Нормировка = 10 ^–1 ∙ . Первый граничный корень 8 (8 ³ = 512). Второй граничный корень 9 (9 ³ = 729). Диапазон 512<714<729.

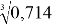
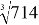
Искомое значение: ≈ 10 ^–1 ∙ (9–15/217) ≈ 0,893 /+0.09 %

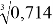
Логику рассуждений при выполнении операций деления и извлечения корней можно проследить в примерах вычислений, приведенных в табл.1.

Таблица 1

Приближенное деление и извлечение корней 2-й и 3-й степени

Опера ­ ция	Нормировка		Границы интервала		Диапазон аргумента		Интер ­ поляция	Итог	Погреш ­ ность
5000/87	1	5000/87	58	57	5046	4959	57,5	57,5	0,05 %
1/17	10 –3	1000/17	59	58	1003	986	58,8	0,0588	0,00 %
1/815	10 –4	1000/82	12	13	984	1066	12,2	0,00123	0,24 %
149,3/0,247	10 +1	1510/25	60	61	1500	1525	60,4	604	-0,08 %
2,6/0,745	10 –1	2620/75	35	34	2625	2550	34,9	3,49	0,00 %
√1000	1	√1000	32	31	1024	961	31,6	31,6	-0,07 %
√5531	1	√5531	75	74	5625	5476	74,4	74,4	0,04 %
√6	10 –1	√600	25	24	625	576	24,5	2,45	0,02 %
√0,00541	10 –3	√5410	74	73	5476	5329	73,5	0,0735	-0,07 %
√5564180	10 +2	√556	24	23	576	529	23,6	2360	0,05 %
3 √2000	1	3√2000	12	13	1728	2197	12,6	12,6	0,01 %
3 √1,715	10 –1	3√1715	12	11	1728	1331	11,97	1,197	0,00 %
3 √0,1487	10 –1	3√149	5	6	125	216	5,26	0,526	-0,72 %

Успех вычислений во многом зависит от навыков безошибочного определения порядка (степени) результата при нормировке, уверенного владения приемами четырехзначной арифметики и линейной интерполяции.

Задача 2. Автомобиль движется со скоростью 40 км/ч. Его обгоняет другой такой же автомобиль, двигаясь со скоростью 60 км/ч. Когда они поравнялись, впереди появилось неожиданное препятствие. Оба водителя начали экстренное торможение, при этом первый автомобиль остановился вплотную к препятствию. Найти скорость второго автомобиля в момент столкновения.

Решение. Из курса физики известно, что при торможении кинетическая энергия переходит в работу по преодолению сил трения mV ₁ ² /2 = А _ТР = μ mgS . Так как автомобили одинаковы, то на одинаковом участке тормозного пути, второй автомобиль потеряет такую же часть энергии, что и первый. Скорость второго автомобиля V в момент столкновения найдем по его остаточной кинетической энергии: mV ² /2 = mV ₂ ² /2 — mV ₁ ² /2 , т. е.

V ₂ = = т. е. V ₂ ∈ (45; 44), т. к. 45 ² =2025; 44 ² =1936, =>

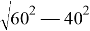
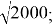
V ₂ ≈ 45–25/89 ≈ 44,7 км/ч.

Тригонометрические функции. Навыки приближенных вычислений тригонометрических функций наиболее востребованы в инженерной области: в задачах пространственного конструирования, при измерении свойств материальных объектов, передаче энергии и информации на основе использования волновых процессов и т. д.

При работе с тригонометрическими функциями особое значение имеет константа π , лежащая в основе множества пространственных преобразований и равная отношению длины окружности к ее диаметру. Значение числа π , приблизительно равное 3,14 1593 легко запомнить, используя сочетание 3,14 и 1593 г. — год опубликования французским математиком Франсуа Виетом широко известной формулы Виета [4] для вычисления числа π :

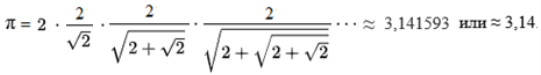
Наиболее простой способ приближенного нахождения значений тригонометрических функций — графический, на основе применения тригонометрического круга. Обычно бывает достаточно положительных значений, описываемых первой четвертью круга (см. рис. 4). Масштабная сетка вполне позволяет получить два верных знака при любых углах.

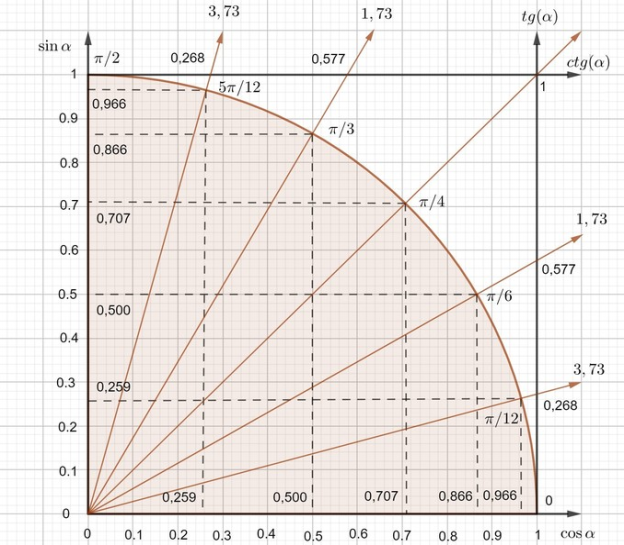
Рис. 4. Фрагмент тригонометрического круга в интервале от 0 до π /2

Тригонометрический круг легко запоминается. Мысленно представляя перед собой его графическое изображение, можно с достаточной точностью находить значения тригонометрических функций на основе освоенных ранее приемов линейной интерполяции. Для этого полезно знать на память значения синуса и тангенса характерных углов, приведенные в табл. 2, а также базовые соотношения между градусной и радианной мерой:

1 радиан = 180 ⁰ /π ≈ 57,3 ⁰ ; 1 ⁰ = π/180 ⁰ /π ≈ 0,01745 радиана.

С помощью линейной интерполяции значение синуса можно вычислить с точностью около одного процента. Косинус следует находить через синус дополнительного угла. Погрешность приближенного нахождения синуса и косинуса интерполяцией будет всегда отрицательной, т. к. при этом дуга окружности фактически заменяется ломаной линией.

Таблица 2

Точные и приближенные значения синуса и тангенса характерных углов

Угол		Синус		Тангенс
Радианы	Градусы	Точно	Прибл.	Точно	Прибл.
π/12	15	(√6 – √2) / 4	0,259	2 – √3	0,268
π/6	30	1 / 2	0,500	√3 / 3	0,577
π/4	45	√2 / 2	0,707	1	1,00
π/3	60	√3 / 2	0,866	√3	1,73
5π/12	75	(√6 +√2) / 4	0,966	2 + √3	3,73

Эту особенность выгодно использовать при приближенном вычислении тангенса в виде отношения синуса к косинусу. Затраты на двойную интерполяцию вполне окупаются значительным повышением точности. Аналогично вычисляется значение котангенса. Прямая интерполяция по значениям тангенса, указанным в таблице 4, возможна при углах не более 45 %. При этом погрешность может достигать нескольких процентов. Полезными для вычислений могут оказаться также следующие формулы:

ctg a = ; arctg a = arcctg .

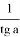
Существенно облегчает вычисления свойство малых углов (менее 0,16 радиана ≈ π/20 ≈ 10 ⁰ ), которое гласит, что «синус малого угла примерно равен его тангенсу и самому углу π в радианах» — погрешность не превышает 1 %. Для углов, близких к 0 или к π /2, зачастую требуется более высокая точность, которую можно достичь, применяя формулы:

cos a = ; sin a = .

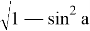
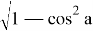
Разберем ряд приемов нахождения тригонометрических функций.

Графический, с помощью тригонометрического круга:

sin 50 ⁰ ≈ 0,82, (примерно 1/3 интервала от 45 ⁰ до 60 ⁰ ); /+0,10 %

tg (1/2)≈ 0,55 , (примерно на 1,5 градуса менее 30 ^0– 57,1 ⁰ /2); /+0,68 %

сtg 36 ⁰ ≈ 1,37 (обратная величина от tg 36 ⁰ ≈ 0,73). / -0,46 %

Графический прием следует применять осторожно, так как уже второй знак результата может оказаться неверным из-за погрешности измерений.

Применение линейной интерполяции:

cos 50 ⁰ ≈ 0,707–5/15*0,207 ≈ 0,638 / -0,04 %

sin 84 ⁰ ≈ 1,0–6/15*0,034 ≈ 0,987 / -0,76 %

tg 50 ⁰ ≈ 1,0 + 5/15*0,73 ≈ 1,243 /+4,30 %

Применение двойной интерполяции:

tg 50 ⁰ = sin 50 ⁰ /cos 50 ⁰ ≈ (0,707+5/15*0,159)/0,638 ≈ 76/64 ≈ 1,20 /+0,69 %

ctg 84 ⁰ ≈ cos 84 ⁰ /sin 84 ⁰ ≈(0,0+6/15*0,259) /0,98 ≈ 104/987 ≈ 0,105 / –0,10 %

Применение двойной интерполяции при нахождении тангенса и котангенса ощутимо снижает погрешность за счет взаимной компенсации погрешностей вычисления синуса и косинуса, в последнем случае с 4 до 0,1 %.

Использование свойства малых углов:

sin (1/5) ≈ 0,2 (почти малый угол); /+0,67 %

cos(1/10) = ≈ ≈ ≈ 0,995 / 0,00 %

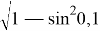
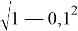
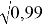
cos 84 ⁰ = sin (90 ⁰ – 84 ⁰ ) = sin (π/30)≈ 3,142/30 ≈ 0,1047; /+0,16 %

sin 84 ⁰ =

≈ ≈ ≈ 0,995 /+0,05 %

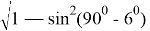
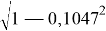
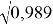
tg 10 ⁰ = tg (π / 18) ≈ 3,142/18 ≈ 0,175. / -0,75 %

arctg 10 = arсctg (1/10) = (π/2–0,1) ≈ (90 ^0– 5,71 ⁰ ) ≈ 84,3 ⁰ /+0,10 %

В конструкторских работах, особенно в вариантном проектировании не требуется столь высокая точность. Однако владение указанными приемами позволяет быстро и эффективно принимать конструктивные решения.

Задача 3. Рассчитать угол подъема на спутник (угол места ϰ , см. рис. 5) для антенны спутниковой связи, монтируемой в г. Усмань, Липецкой области.

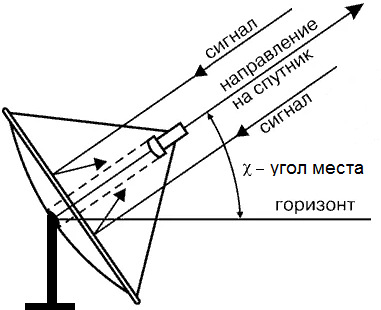
Рис. 5. Установка спутниковой антенны

Решение . Ось приема сигнала должна совпадать с направлением на спутник (см. рис. 5). Если пренебречь разностью долготы спутника и точки приема сигнала, то угол места ϰ можно вычислить по приближенной формуле:

ϰ = arctg ,

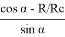
где α — широта точки приема: г. Усмань, координаты: 52 ⁰ СШ, 40 ⁰ ВД;

R/R _c — отношение радиус Земли (≈ 6400 км) к радиусу геоцентрической орбиты спутника (≈42000 км), т. е. R/ R _c ≈ 6400/42000 ≈ 0,152.

cos 52 ⁰ = sin 38 ⁰ ≈ 0,5 + 8∙(0,707–0.5)/15 ≈ 0,5 + 0,11 ≈ 0,61

sin 52 ⁰ ≈ 0,707 + 7∙(0,866–0,707)/15 ≈ 0,707 + 7∙0.159/15 ≈ 0,78

ϰ ≈ arctg ≈ arctg ≈ arctg 0,59, т. е. ϰ ∈ (30 ⁰ ; 45 ⁰ ),

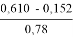
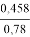
=> ϰ ≈ 30 ⁰ + (0,59–0,577) ∙15 ⁰ /(1–0,577) ≈ 30 ⁰ + 0,013∙15 ⁰ /0,423 ≈ 30,5 ⁰ .

Точная настройка выполняется уже по качеству принимаемого изображения.

Логарифмирование. В естественных науках (особенно в информатике и экономике) логарифмы востребованы почти на уровне тригонометрических функций. Характерной особенностью протекания природных процессов во времени является принцип пропорциональности прироста измеряемой величины самой этой величине. Эта специфика изменений во времени делает логарифмическую функцию удобной, например, в информатике — для описания информационной энтропии (формула Шеннона), в экономике (проценты по вкладам, кредитование), в статистической термодинамике (формула Планкадля энтропии вещества) и т. д. Освоение методов приближенного вычисления логарифмов облегчает решение подобных задач.

Логарифмирование — это операция отыскания показателя степени x , в которую надо возвести основание a , чтобы получить значение аргумента b . Иными словами, это решение уравнения вида a ^x = b . Традиционно записывается в форме x = log _a b , предложенной Джоном Непером в 1614 году. Из сказанного следует, что по сути логарифмирование есть операция, обратная возведению в степень. По аналогии с извлечением корней, операцию логарифмирования можно было бы назвать извлечением степени x из числа b по основанию a , в чем, собственно, и заключается смысл логарифмирования.

Прежде чем приступить к освоению практических приемов приближенного вычисления логарифмов вспомним некоторые свойства показательных функций, а именно:

— Любое число в степени ноль равно единице: a ⁰ = 1 ;

— Произведение a ^b ∙ a ^c = a ^{b + c} ;

— Частное a ^b / a ^c = a ^b-c ;

и вытекающих из них формул для логарифмов:

— Логарифм по любому основанию от единицы равен нулю: log _a 1 = 0 ;

— Логарифм произведения log _a (b∙с) = log _a b + log _a с ;

— Логарифм частного log _a (b/с) = log _a b — log _a с .

Поскольку нас интересует вопрос приближенного нахождения численных значений логарифмов, как операций, обратных возведению в степень, исключительно в целях сокращения промежуточных записей заменим традиционную форму обозначения x = log _a b на упрощенную запись _а b = x , ассоциирующуюся с привычной операцией возведения в степень b = a ^x , то есть будем считать, что следующие обозначения тождественны:

log _a b ≡ _a b

Нам представляется, что допущенная вольность облегчит устные операции за счет сокращения записи. Итак, при вычислении численного значения логарифма перед нами стоит задача определить, на сколько порядков (степеней) число, стоящее за признаком логарифма, больше (или меньше) основания. Рассмотрим ряд практических приемов.

Применение линейной интерполяции .

Логарифм по основанию 5 из 1500, т. е. log ₅ (1500) .

— Пусть 1-я граничная степень равна 4, т. е. 5 ⁴ = 625.

— Пусть 2-я граничная степень равна 5, т. е. 5 ⁵ = 3125.

— Искомая степень ≈ 4 + 875/2500 ≈ 4,35. Или сокращенно:

₅ 1500 ∈ (4; 5), т. к. 5 ⁴ = 625; 5 ⁵ =3125, => ₅ 1500 ≈ 4+1∙875/2500 ≈ 4,35 /-4,3 %

Логарифм по основанию 5 из 1,5, т. е. log ₅ (1,5), или сокращенно:

₅ 1,5 ∈ (0; 1), т. к. 5 ⁰ = 1; 5 ¹ = 5, => ₅ 1,5 ≈ 0+1∙0,5/4 ≈ 0,125 /-50 %

Высокая погрешность в последнем примере объясняется сильной кривизной логарифмической функции на интервале от 0 до ±1. Точность можно повысить уменьшением границ интервала, например, до

≈ 1,71:

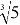
₅ 1,5 ∈ (0; 1/3), т. к. 5 ⁰ =1; 5 ^1/3 ≈ 1,71, => ₅ 1,5 ≈ 0+(1/3)∙0,5/0,71 ≈ 0,235 /-6,7 %

Применение формул логарифма произведения (частного) .

Рассмотрим снова логарифм по основанию 5 из 1500 .

— Представим число 1500 в виде произведения 1500 ≈ 625∙2,4.

— Тогда ₅ 1500 ≈ ₅ 625 + ₅ 2,4 ≈ 4 + ₅ 2,4.

— ₅ 2,4 ∈ (1/2; 1), т. к. 5 ^1/2 ≈ 2,24; 5 ¹ = 5, => ₅ 2,4 ≈ 0,5+0,16∙0,5/2,76 ≈ 0,53.

— Искомая степень ≈ 4 + 0,53 ≈ 4,53 /-0,31 %

Особенности вычисления десятичных логарифмов.

Десятичный логарифм ( log ₁₀ или lg ) отличается высокой кривизной функции, поэтому для приближенных вычислений с удовлетворительной точностью на интервале (0; ±2) желательно иметь ряд дополнительных граничных точек ( ¹⁰ ≈ 1,26 ; ⁴

≈ 1,78 ; ≈ 2,15 ; ≈ 3,16 ; 10 ≈ 31,6 ).

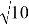
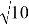
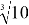
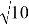
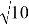
Десятичный логарифм от 1500, т. е. log ₁₀ 1500 = lg 1500, сокращенно:

₁₀ 1500 = ₁₀ (1000∙1,5) = 3 + ₁₀ 1,5; ₁₀ 1,5 ∈ (0,1; 0,25), т. к. 10 ^1/10 ≈1,26; 10 ^1/4 ≈1,78,

=> ₁₀ 1500 = 3 + ₁₀ 1,5 ≈ 3 + (0,1 + 0,24∙0,15/0,54) ≈ 3,17 /-0,19 %

Десятичный логарифм от 2,72, т. е. log ₁₀ 2,72 = lg 2,72, сокращенно:

₁₀ 2,72 ∈ (1/2; 1/3), т. к. 10 ^1/2 ≈ 3,16; 10 ^1/3 ≈ 2,15,

=> ₁₀ 2,72 ≈ 0,5–0,34 ∙ 0,167/1,01 ≈ 0,444 /-2,2 %

Десятичный логарифм от 0,318, т. е. log ₁₀ 0,318 = lg 0,318, сокращенно:

₁₀ 0,318 = ₁₀ (1/3,14)= 0 _{– 10} 3,14; ₁₀ 3,14 = ∈ (1/3; 1/2), т. к. 10 ^1/3 ≈2,15; 10 ^1/2 ≈3,16,

=> ₁₀ 0,318 = 0 _{– 10} 3,14 ≈ 0 — (0,5–0,02∙0,17/2,01) ≈ — 0,498 /-0,22 %

При интерполяции участок логарифмической кривой заменяется отрезком прямой линии, что всегда приводит к отрицательной погрешности, которую при соответствующих навыках можно корректировать вручную.

Особенности вычисления бинарных (двоичных) логарифмов.

Основное применение бинарных логарифмов — в информатике и комбинаторике, где их значения обычно лежат за пределами интервала (0; ±1). Для их вычисления достаточно уметь возводить 2 в целую степень.

Бинарный логарифм от 1500, т. е. log ₂ 1500 = lb 1500, или сокращенно:

₂ 1500 ∈ (10; 11), т. к. 2 ¹⁰ =1024; 2 ¹¹ =2048,=> ₂ 1500 ≈ 10+500/1024≈10,5 /-1,1 %

Значения бинарных логарифмов в интервале (0; ±2) требуются значительно реже. Для их нахождения можно воспользоваться следующими граничными точками: ¹⁰ ≈ 1,07 ; ⁴ ≈ 1,19 ; ³ ≈1 ,26 ;

≈ 1,414 .

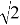
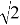
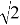
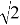
Бинарный логарифм от 2,72, т. е. log ₂ 2,72 = lb 2,72, сокращенно:

₂ 2,72 = ₂ (2∙1,36)= 1 + ₂ 1,36; ₂ 1,36 = ∈ (1/3; 1/2), т. к. 2 ^1/3 ≈1,26; 2 ^1/2 ≈1,41,

=> ₂ 2,72 = 1 + ₂ 1,36 ≈ 1 + (0,33 + 0,1∙0,17/0,15) ≈ 1,44 /-0,25 %

Бинарный логарифм от 0,318, т. е. log ₂ 0,318 = lb 0,318, сокращенно:

₂ 0,318 = ₂ (1/3,14) = ₂ (0,5/1,57) = ₂ (1/2) — ₂ 1,57 = 0–1 — ₂ 1,57;

₂ 1,57 = ∈ (1/2; 1), т. к. 2 ^1/2 ≈ 1,41; 2 ¹ =2, => ₂ 1,57 ≈ 0,5 + 0,16∙0,5/0,59 ≈ 0,64,

=> ₂ 0,318 = 0–1 — ₂ 1,57 ≈ -1–0,64 ≈ -1,64 /-0,78 %

Особенности вычисления натуральных логарифмов.

Основанием натурального логарифма ( log _e или l n ) служит такое число e , при котором производная от натурального логарифма в любой точке равна обратной функции (ln x)’ =1/x . Это оказалось удобным для математических преобразований, благодаря чему натуральный логарифм и нашел широкое применение в различных областях. Запомнить константу e ≈ 2,7 18281828 не трудно 2,7 + 1828 + 1828 (например: 2,7 метра — оптимальная высота жилья человека и 1828 — год рождения Л. Н. Толстого). Кстати, комфортным для спальни считается объем, примерно равный e ³ , т. е. 20 кубических метров. Численное значение константы е можно вычислить с помощью ряда:

е = 1 + 1/1! + 1/2! + 1/3! +... ≈ 2,7 1828182846 или ≈ 2,72 .

Нахождение экспоненты e ^x вручную достаточно трудоемко, поэтому для приближенного вычисления лучше воспользоваться уже освоенной техникой вычисления бинарных и десятичных логарифмов, а затем перейти к натуральному через соответствующие переходные модули:

ln (x) = lg (x) / lg (e) ≈ lg (x) / 0,434 ≈ 2,3 ∙ lg (x),

ln (x) = lb (x) / lb (e) ≈ lb (x) / 1,44 ≈ 0,7 ∙ lb (x).

Примеры приближенного вычисления натуральных логарифмов:

Натуральный логарифм от 10 т. е. log _e 10 = ln 10, методом интерполяции:

_е 10 ∈ (2; 3), т. к. е ² ≈ 7,4; е ³ ≈ 20, => _е 10 ≈ 2 + 2,6∙1/12,6 ≈ 2,21 /-4,0 %

log _e 10 = ln 10 через переходный модуль десятичного логарифма:

_е 10 ≈ 2,3 ∙ ₁₀ 10 ≈ 2,3∙1 = 2,3 /0,00 %

log _e 1500 = ln 1500 через переходные модули:

_е 1500 = 2,3 ∙ ₁₀ 1500 ≈ 2,3∙3,17 (см. ранее) ≈ 7,30 /-0,18 %

_е 1500 = 0,7 ∙ ₂ 1500 ≈ 0,7∙10,5 (см. ранее) ≈ 7,35 /+0,50 %

Задача 4. Предприятие состоит из головного офиса, где работают 80 сотрудников и двух филиалов по 20 работников. Для объединения компьютеров в единую ЛВС выделена ip-сеть 192.168.1.0/24 (24-короткая маска). Требуется разбить ее на подсети для головного офиса и филиалов.

Решение. Полное адресное пространство сети 192.168.1.0/24–256 адресов.

Половину адресного пространства выделяем под головной офис. Вычисляем короткую маску: 24 + lb (256/128) = 24+1 = 25 и записываем ip-адрес подсети 192.168.1.0/25. Два адреса резервируются под маршрутизатор и широковещательные запросы, 80 — по 1 на сотрудника и 46 — в резерв.

Выделяем по 32 адреса под каждый филиал. Вычисляем короткую маску: 24 + lb (256/32) = 24+3 = 27 и записываем ip-адреса подсетей филиалов: 192.168.1.128/27 и 192.168.1.160/27. Итого в каждом филиале будет доступно по 20 адресов для устройств сотрудников и по 10 адресов в резерве. Еще 64 адреса останется на развитие филиальной сети.

Задача 5. Сколько времени потребуется частному инвестору, месячный доход которого от торговли на бирже составляет 10 %, чтобы заработать на квартиру стоимостью 7 млн рублей при начальном капитале 1 млн руб.?

Решение . Чтобы добиться цели, инвестору нужно примерно 8 млн. руб., тогда после уплаты 13 % налога у него останется нужная сумма 8 — (8–1) ∙ 0,13 ≈ 7,1 млн. руб. Составим уравнение сложного процента: 1 ∙ 1,1 ^x = 8. Возьмем логарифм с обеих частей уравнения. Обычно берут десятичный логарифм, но поскольку в правой части стоит удобное число 8 = 2 ³ , мы возьмем бинарный:

x ∙ lb 1,1 = lb 8, => x = lb 8 / lb 1,1 = 3 / lb 1,1.

₂ 1,1 ∈ (0,1; 0,25) => ₂ 1,1 ≈ 0,1 + 0,03 ∙ 0,15/0,12 ≈ 0,135; x ≈ 3 / 0,135 ≈ 22.

Итак, при начальном капитале в 1 миллион рублей и ежемесячной доходности в 10 % инвестору потребуется около 2 лет (≈22 месяца).

Заключение. Проведенное исследование дает основание утверждать, что владение навыками линейной интерполяции и четырехзначной арифметики позволяет быстро и без калькулятора выполнять различные математические операции, включая тригонометрические и логарифмирование. В работе сформулирован набор приемов, упрощающих устные, либо ручные вычисления различной сложности с точностью до двух-трех верных знаков. Продемонстрирована эффективность применения предложенной техники приближенных расчетов на примерах решения различных задач из инженерной и экономической практики.

Изложенные приемы могут быть полезны инженерно-техническим работникам и студентам вузов технических и экономических специальностей.

Литература:

1. Арутюнян Е., Левитас Г. Занимательная математика. — М.: АСТ-ПРЕСС, 1999. — 368 с.
2. Гарднер М. Математические чудеса и тайны. — М.: Наука, 1978. — 128 с.
3. Дудина М. М., Глотова Е. Е. Изучение требований работодателей к выпускникам вузов: российский и зарубежный опыт // Гуманитарные исследования, 2015. — № 1 (5). — стр. 95–98. — URL: https://cyberleninka.ru
4. История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. Том.1 — М.: Наука, 1970. — стр. 314–315.
5. Камаев П. М. Устный счет, 2007. — стр. 4–29.
6. Trachtenberg, Yakow, The Trachtenberg’s Speed System of Basic Mathematics, 2004. — 207 p.
7. Will Archer, Jess Davison. Graduate Employability: What Do Employers Think and Want? /Council for Industry and Higher Education. London — 2008. — 20 p.