Логарифмические уравнения и неравенства в итоговой аттестации выпускников

В современных реалиях изучения математики такое понятие, как «логарифм», вызывает у учащихся сложности в понимании еще на начальных этапах. Ввиду этих трудностей, у учащихся возникают проблемы с изучением последующих тем с логарифмами, в частности уравнений и неравенств с логарифмами. Данную тему нельзя оставить без должного внимания.

Ключевые слова: логарифмическое уравнение, логарифмическое неравенство, итоговая аттестация, внеурочная деятельность.

Тема «Логарифмические уравнения и неравенства» занимает важное место в курсе математики старшей школы, являясь при этом неотъемлемой частью итоговой аттестации выпускников. Овладение этой темой необходимо не только для рационального освоения курса алгебры и начал математического анализа, но и для подготовки к успешной сдаче Единого Государственного Экзамена (ЕГЭ) и иных форм контроля.

Овладение методикой решения логарифмических уравнений способствует повышению умственных и творческих способностей учащихся, обогащению математической культуры учащихся и более глубокому и осознанному усвоению учебного материала.

При изучении логарифмических уравнений необходимо рассмотреть методы решения:

— по определению логарифма (метод подойдет для решения уравнений вида , то есть, для решения простейших логарифмических уравнений);

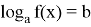
— по свойствам логарифма (используется для уравнений, содержащих сумму или разность логарифмов, или же степени в аргументе или основании логарифма);

— с помощью операции потенцирования (избавление от логарифма; метод применим, если имеем равенство двух логарифмов по одинаковому основанию);

— метод введения новой переменной (метод, применяемый при решении уравнений, содержащих несколько одинаковых логарифмов или же логарифмов в некоторой степени);

— функционально-графический метод (рассматриваются уравнения на функциональном уровне, рассматриваются свойства функции, построение графика).

Важно отметить, что чаще всего уравнения, как и неравенства, решаются сразу несколькими методами, которые дополняют друг друга.

Обратимся к теме «Логарифмические неравенства». В дополнение к основному материалу данной темы необходимо дать учащимся определение понятий «следствие» и «равносильность», поскольку при решении неравенств очень важно соблюдать равносильность преобразований; в противном случае, это может привести к потере решений. И еще одним важным пунктом при решении логарифмических неравенств считается нахождение области допустимых значений логарифмов, при этом рекомендуется начинать решение с нахождения ОДЗ.

Методы решения логарифмических неравенств перекликаются с методами решения логарифмических уравнений (по определению логарифма, по свойствам логарифма, с помощью операции потенцирования, метод введения новой переменной, с помощью операции логарифмирования функционально-графический метод), но при этом дополняются:

— методом интервалов (основан на разбиении числовой прямой на промежутки (интервалы), на каждом из которых выражение имеет свой знак; чаще всего применяется при решении дробно-рациональных неравенств);

— методом рационализации (переход от сложных неравенств к более простым рациональным выражениям);

— методом мажорант (метод оценок), который применим при решении нестандартных неравенств, которые не получается решить классическими базовыми методами.

Между методами решения логарифмических уравнений и логарифмических неравенств есть существенные отличия: при решении неравенств необходимо учитывать монотонность соответствующей логарифмической функции в зависимости от величины ее основания.

Логарифмические уравнения и неравенства обязательны к изучению каждого выпускника, поскольку задания по этой теме встречаются в итоговой аттестации как на базовом, так и на профильном уровнях. На рис. 1. представлены типы таких заданий. Ввиду того, что задания с неравенствами, как правило, вызывают больше трудностей, нежели остальные вышеперечисленные задания, мы проанализируем более подробно задание № 15 ЕГЭ по математике (профильный уровень).

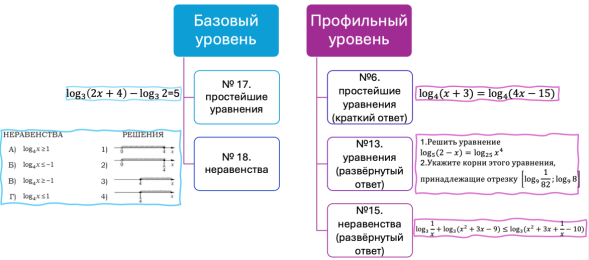
Рис. 1. Типы заданий в итоговой аттестации

Согласно нормативным документам об итогах единого государственного экзамена на территории Ростовской области за 2018, 2019, 2020, 2023 годы, нами был проведён анализ статистики выполнения логарифмического неравенства (8,8 %; 16,9 %; 14,9 %; 18 % соответственно). Как можно заметить, за последние шесть лет логарифмы в неравенствах встречаются довольно часто, что свидетельствует о том, что этому типу неравенств следует уделять большое внимание при подготовке к итоговой аттестации. При этом процент выполнения данного задания колеблется, что говорит о нестабильном усвоении учащимися темы «Логарифмические уравнения и неравенства».

По результатам анализа современных учебников по алгебре и началам математического анализа за 10–11 классы, входящих в федеральный перечень учебников (ФПУ) [5], можно сделать вывод, что в них достаточно материала для старшеклассника для качественного изучения данных тем. Однако ни в одном из них нет полной классификации методов решения уравнений и неравенств. Мы ознакомились со следующими учебными пособиями: Мерзляк А. Г. 10–11 классы (углублённый уровень) [3], [4] и Алимов Ш. А. 10–11 классы [1]. В учебнике Мерзляка А. Г. данная тема освещается в 11 классе, поэтому, в качестве проведения сравнительного анализа, нами также был проанализирован учебник 11 класса базового уровня [2]. В ходе анализа были выявлены отличия в сложности и объёме практических заданий: учебник углублённого уровня содержит все задания из учебника базового уровня с добавлением 40–60 % заданий повышенной сложности.

По результатам проверки работ выпускников за последние годы итоговой аттестации, можно отметить следующие часто допускаемые ошибки: неравносильность преобразований, ошибка в применении свойств, упущение или некорректность ОДЗ, некорректное введение замены переменной. Во избежание этих и других ошибок можно провести с учащимися модуль курса внеурочной деятельности в рамках подготовки к итоговой аттестации выпускников.

Программа модуля курса внеурочной деятельности «Уравнения и неравенства с логарифмами» может быть следующей:

Данный модуль курса способствует качественной и эффективной подготовке к итоговой аттестации, разработан для учащихся 11 класса в качестве дополнительного изучения материала, поскольку подготовка к экзамену требует долгой, упорной и плодотворной работы, помимо изучения в рамках школьной программы. Программа курса также включает материалы и для самостоятельного закрепления материала. Например, разработанные карточки для запоминания свойств (рис. 2) и электронный Google-тест (рис. 3).

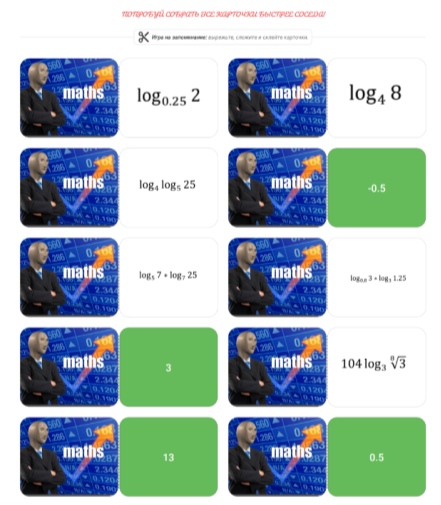
Рис. 2. Карточки для запоминания свойств

Рис. 3. Google-тест

Таким образом, тема «Логарифмические уравнения и неравенства» обязательна к изучению учащимися 10–11 классов, поскольку задания по этой теме встречается на всех уровнях ЕГЭ. В учебных пособиях, используемых школьниками, имеется весь необходимый материал и достаточное количество тренировочных заданий. Модуль курса внеурочной деятельности может быть использован в качестве дополнения к подготовке учащихся к итоговой аттестации педагогами образовательных школ и дополнительного образования.

Литература:

1. Алимов Ш. А., Колягин Ю. М., Ткачева М. В. и другие. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10–11кл. — М.: Просвещение, 2016.
2. Мерзляк А. Г., Номировский Д. А., Поляков В. М., под редакцией Подольского B. E. Математика. Алгебра и начала математического анализа. 11 класс. Базовый уровень. — М.: Вентана-граф, 2019.
3. Мерзляк А. Г., Номировский Д. А., Поляков В. М., под редакцией Подольского B. E. Математика. Алгебра и начала математического анализа. 10 класс. Углублённый уровень. — М.: Вентана-граф, 2019.
4. Мерзляк А. Г., Номировский Д. А., Поляков В. М., под редакцией Подольского B. E. Математика. Алгебра и начала математического анализа. 11 класс. Углублённый уровень. — М.: Вентана-граф, 2019.
5. Федеральный перечень учебников // Группа компаний «Просвещение» URL: https://events.prosv.ru/uploads/2022/11/additions/JGMFoiav44UWjhw77aeys0iW84dQ3RkREL8pLmLr.pdf (дата обращения: 06.05.2024).