Введение в алгебраические уравнения объясняет, что алгебраическое уравнение — это уравнение, в котором используются алгебраические выражения, содержащие переменные и операции сложения, вычитания, умножения и возведения в степень. Различные типы алгебраических уравнений включают линейные, квадратные, кубические и т. д., в зависимости от степени переменной. Алгебраические уравнения имеют большое значение как в математике, так и в реальной жизни, например, для решения физических задач или моделирования экономических процессов.
Методы решения линейных уравнений представляют собой основные принципы, которые позволяют найти значения переменных, удовлетворяющие уравнению. Примеры линейных уравнений и их решений помогают понять применение этих методов, а графическое представление линейных уравнений позволяет визуализировать их геометрическое значение.
Методы решения квадратных уравнений основаны на формуле дискриминанта, которая позволяет определить количество и тип корней уравнения. Примеры квадратных уравнений и их решений помогают разобраться в использовании этой формулы, а графическое представление квадратных уравнений позволяет увидеть геометрическую интерпретацию корней.
Методы решения кубических уравнений представляют собой общий подход к решению уравнений третьей степени. Примеры кубических уравнений и их решений помогают понять этот подход, а использование специальных формул позволяет решить некоторые кубические уравнения более эффективно.
Метод матриц и определителей является одним из методов решения систем линейных уравнений. Он основан на использовании матриц и их определителей для нахождения решения системы.
Для начала систему линейных уравнений можно записать в матричной форме, где коэффициенты перед неизвестными образуют матрицу, а значения правой части уравнений образуют столбец. Например, система уравнений:
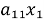
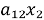
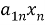
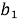
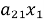
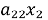
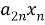
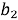
...
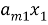
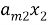
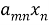
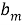
может быть записана в виде:
AX = B
где A — матрица коэффициентов, X — столбец неизвестных, B — столбец значений правой части. Для решения системы с помощью метода матриц и определителей, необходимо вычислить определитель матрицы коэффициентов A. Если определитель не равен нулю, то система имеет единственное решение, которое может быть найдено с помощью формулы Крамера:
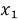
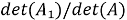
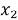
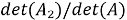
...
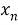
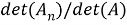
где
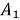
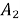
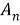
Пример:
Рассмотрим систему уравнений:
2x + 3y = 8
4x — 2y = 2
Записывая ее в матричной форме, получаем:
[2 3] [x] [8]
[4 -2] [y] = [2]
Вычисляем определитель матрицы коэффициентов:
det([2 3]) = 2*(-2) — 3*4 = -14
Так как определитель не равен нулю, система имеет единственное решение. Вычисляем значения неизвестных с помощью формулы Крамера:
x = det([8 3])/det([2 3]) = (8*(-2) — 3*2)/(-14) = -1
y = det([2 8])/det([2 3]) = (2*2–8*(-4))/(-14) = 2
Таким образом, решение системы уравнений равно x = -1, y = 2.
Эти методы решения различных типов уравнений помогают математикам, физикам, инженерам и другим специалистам в различных областях науки и техники решать сложные задачи и моделировать реальные процессы. Они являются важным инструментом для анализа и понимания различных явлений и являются основой для более сложных методов и теорий.
Примеры с решением:
1. Линейное уравнение: 2x + 3 = 7
Решение:
2x + 3 = 7
2x = 7–3
2x = 4
x = 4/2
x = 2
2. Квадратное уравнение: x^2–5x + 6 = 0
Решение:
Используем формулу дискриминанта:
D = b^2–4ac
D = (-5)^2–4(1)(6)
D = 25–24
D = 1
Находим корни уравнения:
x = (-b ± √D) / (2a)
x = (-(-5) ± √1) / (2*1)
x = (5 ± 1) / 2
Таким образом, получаем два корня:
x1 = (5 + 1) / 2 = 6/2 = 3
x2 = (5–1) / 2 = 4/2 = 2
3. Кубическое уравнение: x^3 + 2x^2–5x — 6 = 0
Решение:
Рассмотрим специальную формулу для решения кубических уравнений:
x = ∛(-q/2 + √(q^2/4 + p^3/27)) + ∛(-q/2 — √(q^2/4 + p^3/27))
Где p = -5, q = -6
Подставляем значения:
x = ∛(-(-6)/2 + √((-6)^2/4 + (-5)^3/27)) + ∛(-(-6)/2 — √((-6)^2/4 + (-5)^3/27))
Упрощаем и находим корень:
x = ∛(3 + √(9 + 125/27)) + ∛(3 — √(9 + 125/27))
Таким образом, получаем значение корня кубического уравнения.
Литература:
- Бабенко, К. И. Основы численного анализа / К. И. Бабенко. — М.: Главная редакция физико-математической литературы издательства «Наука», 1986. — 744 c.
- Бакушинский, А. Элементы высшей математики и численных методов / А. Бакушинский, В. Власов. — М.: Просвещение, 2014. — 336 c.
- Босс, В. Лекции по математике. Том 1. Анализ. Учебное пособие / В. Босс. — М.: Либроком, 2016. — 216 c.
- Воробьев, Н. Н. Теория рядов / Н. Н. Воробьев. — М.: Главная редакция физико-математической литературы издательства «Наука», 1986. — 408 c.

