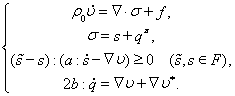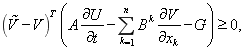Введение
В связи с возросшим интересом к новым материалам с перспективными свойствами, как с экономической, так и с механической точек зрения, большое значение имеет моделирование поведения различных сред под воздействием внешних сил. Металлические пены – представители целого семейства пористых материалов. Их отличительными свойствами являются низкая плотность и высокие прочностные характеристики [1, 2]. Причины, по которым пористые металлы еще не стали очень популярны, заключаются в несовершенстве технологии их производства (сложно получить однородное распределение пор) и высокой стоимостью этой технологии. В результате исследований последних лет наметились значительные изменения, как в совершенствовании методов получения металлических пен, так и в снижении стоимости их производства.
Технология
Получить пористые металлы можно несколькими способами [3]:
введением газа в жидкий сплав с образованием пузырьков нужного размера и их дальнейшей стабилизацией охлаждением;
формированием смеси из порошков металла и вспенивающего материала (например, ![]() ) последующим нагреванием смеси с высвобождением газа
) последующим нагреванием смеси с высвобождением газа ![]() и образованием пузырьков;
и образованием пузырьков;
спеканием полых металлических сфер;
растворением газа в жидком металле под давлением, с контролируемым высвобождением в процессе затвердевания;
заполнением песком полимерного пористого материала с открытыми ячейками с дальнейшим выжиганием полимера и заполнением получившейся формы металлическим сплавом;
покрытием полимерного пористого материала с открытыми ячейками частицами металлического сплава методом электрического осаждения с последующим выжиганием полимера;
задержкой инертного газа в металлическом порошке под высоким давлением и дальнейшим нагреванием с расширением газа;
созданием смеси металла и растворяемого материала, с последующим выщелачиванием.
Все методы производства пористых металлов связаны с высокими температурами и необходимостью точно контролировать изменения температуры и давления на различных стадиях технологических процессов.
Модель
Для описания модели используется реологический метод. На рис. 1 приведена реологическая схема пористой среды [4]. Согласно этой схеме поведение пористого металла до момента схлопывания пор соответствует пружине с модулем упругой податливости ![]() а повышение жесткости после схлопывания пор соответствует второй пружине с модулем
а повышение жесткости после схлопывания пор соответствует второй пружине с модулем ![]() Жесткий контакт соответствует пористости материала и имитирует уплотнение среды. Также эта схема учитывает пластические свойства пористого металла.
Жесткий контакт соответствует пористости материала и имитирует уплотнение среды. Также эта схема учитывает пластические свойства пористого металла.
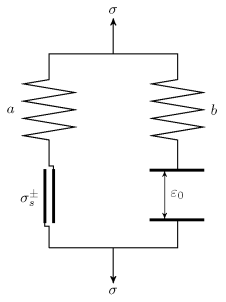
Рис. 1. Реологическая схема
Диаграмма связи между напряжением и деформацией пористой среды при одноосном сжатии изображена на рис. 2.
Процесс упругой деформации материала описывается уравнением ![]() а упругопластической (после схлопывания пор) –
а упругопластической (после схлопывания пор) – ![]() Точка
Точка ![]() соответствует моменту схлопывания пор. Приведенная диаграмма не противоречит результатам практических экспериментов по сжатию пористых металлов [1, 3, 5].
соответствует моменту схлопывания пор. Приведенная диаграмма не противоречит результатам практических экспериментов по сжатию пористых металлов [1, 3, 5].
Используя приведенную выше реологическую схему можно составить следующие определяющие соотношения:
|
|
(1) |
Здесь ![]() – плотность пористого материала;
– плотность пористого материала; ![]() – пористость;
– пористость; ![]() – вектор скорости;
– вектор скорости; ![]() – вектор объемных сил;
– вектор объемных сил; ![]() – оператор Гамильтона;
– оператор Гамильтона; ![]() – сопряженный тензор. Используются механические характеристики пористого материала: модули упругой податливости
– сопряженный тензор. Используются механические характеристики пористого материала: модули упругой податливости ![]()
![]() и определяющие их модули сдвига
и определяющие их модули сдвига ![]()
![]() ; модули объемного сжатия
; модули объемного сжатия ![]()
![]() ; предел текучести среды
; предел текучести среды ![]() ; начальная пористость
; начальная пористость ![]() , вычисленные для материала с малой пористостью в работе [6]. Искомыми функциями являются вектор скорости
, вычисленные для материала с малой пористостью в работе [6]. Искомыми функциями являются вектор скорости ![]() и тензоры
и тензоры ![]() и
и ![]()
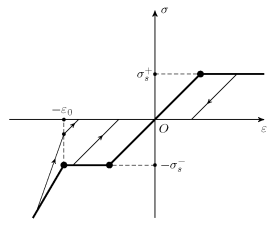
Рис. 2. Диаграмма связи между напряжением и деформацией
Полагая ![]() после скалярного умножения обеих частей уравнения движения на вектор скорости двойной свертки дифференциального уравнения для
после скалярного умножения обеих частей уравнения движения на вектор скорости двойной свертки дифференциального уравнения для ![]() с тензором
с тензором ![]() и суммирования результатов, получим неравенство внутренней диссипации энергии:
и суммирования результатов, получим неравенство внутренней диссипации энергии:
![]()
Левая часть неравенства представляет собой скорость изменения кинетической и потенциальной энергий, а правая – мощность внутренних поверхностных и активных объемных сил. Разность между правой и левой частями равна скорости пластической диссипации энергии, которая в соответствии с принципами необратимой термодинамики не может быть отрицательной величиной. При выводе данного неравенства существенно использовалось тождество [4]:
![]()
которое справедливо для проекции на произвольный выпуклый конус.
Вычислительный алгоритм
Чтобы построить алгоритм численной реализации описанной модели, представим соотношения (1) в виде вариационного неравенства в матричной форме:
|
|
(2) |
Здесь ![]() – символ транспонирования;
– символ транспонирования; ![]() – размерность модели;
– размерность модели; ![]() – вектор массовых сил;
– вектор массовых сил; ![]() и
и ![]() – вектор-функции, содержащие компоненты вектора скорости и тензоров напряжений. Для трехмерного случая:
– вектор-функции, содержащие компоненты вектора скорости и тензоров напряжений. Для трехмерного случая:
![]()
![]()
Матрицы-коэффициенты из вариационного неравенства (2) представимы следующим образом:
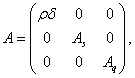
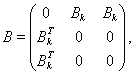
где ![]() – единичная матрица
– единичная матрица ![]()

![]() аналогично состоит из компонентов тензора упругой податливости
аналогично состоит из компонентов тензора упругой податливости ![]()
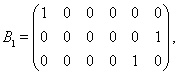


При ![]() вариационное неравенство (2) соответствует модели уплотненного состояния пористого металла.
вариационное неравенство (2) соответствует модели уплотненного состояния пористого металла.
Для решения задачи деформирования пористой среды использован явный по времени алгоритм численной реализации метода сквозного счета с использованием метода расщепления по физическим процессам. На каждом шаге по времени решается задача деформирования упругой пористой среды:
|
|
(3) |
используя метод двуциклического расщепления по пространственным переменным [7]. Для трехмерного случая на интервале ![]() метод расщепления состоит из следующих этапов:
метод расщепления состоит из следующих этапов:
решение одномерной задачи в направлении ![]() на интервале
на интервале ![]()
решение одномерной задачи в направлении ![]() на интервале
на интервале ![]()
решение одномерной задачи в направлении ![]() на интервале
на интервале ![]()
повторный пересчет в направлении ![]() на интервале
на интервале ![]()
повторный пересчет в направлении ![]() на интервале
на интервале ![]()
повторный пересчет в направлении ![]() на интервале
на интервале ![]()
Расщепление системы уравнений (3) дает несколько одномерных систем:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Искомое ![]() равно
равно ![]() Описанный метод обеспечивает устойчивость численного решения при выполнении на всех этапах одномерных условий устойчивости и является методом второго порядка точности (при условии использования на его этапах схем второго порядка). Одномерные системы уравнений на этапах расщепления решаются при помощи явной монотонной схемы "предиктор-корректор".
Описанный метод обеспечивает устойчивость численного решения при выполнении на всех этапах одномерных условий устойчивости и является методом второго порядка точности (при условии использования на его этапах схем второго порядка). Одномерные системы уравнений на этапах расщепления решаются при помощи явной монотонной схемы "предиктор-корректор".
Чтобы учесть пластические свойства металла, вариационное неравенство (2) заменой производной по времени конечной разностью на интервале ![]() приводится к виду:
приводится к виду:
![]()
![]()
где ![]() – решение упругой задачи (3) в момент времени
– решение упругой задачи (3) в момент времени ![]() Для модели пористого металла это неравенство решается достаточно просто [8].
Для модели пористого металла это неравенство решается достаточно просто [8].
Параллельная реализация алгоритма
Расчеты проводятся на многопроцессорной вычислительной системе. Программирование выполнено по технологии SPMD (Single Program – Multiple Data) на языке Fortran-90 с использованием библиотеки MPI (Message Passing Interface). Программа выполняет подобные вычисления, сведенные к согласованной поэтапной реализации метода расщепления по пространственным переменным. Программная реализация алгоритма осложняется необходимостью склейки решений на границах разделения области между вычислительными узлами.
Вычисления выполняются для моделирования деформации блока пористого алюминия с различными значениями пористости ![]() (5 %, 10 %, 25 %).
(5 %, 10 %, 25 %).
Литература:
1. Banhart J., Baumeister J. Deformation Characteristics of Metal Foams // Journal of Materials Science. – 1998. – Vol. 33, Iss. 6. – P. 1431–1440.
2. Gibson L.J., Ashby M.F. Cellular Solids: Structure and Properties, Second Edition // (ISBN: 978-0-521-49911-9). CambridgeUniversity Press, 1997.
3. Gibson L.J. Mechanical Behavior of Metallic Foams // Annual Review of Materials Research. – 2000. – Vol. 30. – P. 191–227.
4. Садовская О.В., Садовский В.М. Математическоемоделированиевзадачахмеханикисыпучихсред. – М.: Физматлит, 2008.
5. Ashby M.F. Plastic Deformation of Cellular Materials. Encyclopedia of Materials: Science and Technology (ISBN: 978-0-08-043152-9). PergamonPress. – 2001. – P. 7068–7071.
6. Золотухин А.В. Численное моделирование свойств пористых металлов // Материалы Всероссийской научно-практической конференции «Актуальные проблемы авиации и космонавтики». – Красноярск: СибГАУ. – 2011. – Т. 1. – С. 138–139.
7. Марчук Г.И. Методы расщепления. – М.: Наука, 1988.
8. Sadovskii V.M., Sadovskaya O.V. Mathematical Modeling of a Metal Foam as an Elastic-Plastic Continuum with Changing Resistance // AIP Conf. Proc. – 2015. – Vol. 1648. – P. 63005-1–63005-4 (DOI: 10.1063/1.4912863).