Математическая модель процесса гибки с растяжением



Комплекс практических задач современного авиастроения, появление новых материалов, конструкций, повышение требований к уровню организации производства и к качеству выпускаемой продукции, ее конкурентоспособности на внешнем и внутреннем рынке определили насущную потребность в современных инновационных технологиях и оборудовании, характеризуемых возможно полной и высокоэффективной автоматизацией производства. К ним обоснованно можно отнести использование автоматизированных профилегибочных машин, в частности для гибки с растяжением длинномерных сложнопрофильных изделий.

Технология авиастроения, обработка авиационных сплавов давлением отличаются повышенной изменчивостью размерно-механических параметров заготовок, мелкосерийностью и многономенклатурностью, значительной сложностью кинематических схем и сложностью проектирования управляющих программ, высоким уровнем (априорной) неопределенности, из-за чего существующие САПР оказываются неэффективными из-за отсутствия времени на своевременную подготовку управляющих программ в условиях быстрой смены номенклатуры деталей и инструментальной оснастки. Последнее обусловило необходимость разработки таких технологий, при которых формообразующее замыкание координат и сил являлось слабозависящим от воздействия влияющих факторов и параметров различной природы за счет подготовки управляющей программы в реальном времени в режиме «Обучение» по первой детали.

Рис. 1. Конструкторско-технологическое членение самолета

В авиастроении процессы гибки с растяжением используются в условиях многономенклатурного мелкосерийного производства. На рис. 1 представлено конструкторско-технологическое членение спортивного самолета, где выделены детали, изготавливаемые гибкой с растяжением. При изготовлении летательного аппарата число деталей из пpофилей может достигать десятков тысяч, общая их длина — до 30 км, pазмеpы деталей от 25 до 1000 мм, их масса может меняться от 0,01 до 25 кг. Характер производства предполагает частую замену (несколько раз за рабочую смену) пуансонов различных типоразмеров и конфигурации, используемых для изготовления деталей. Количество деталей в партии колеблется от 2–3 до 30–40 штук. Вместе с тем существующие системы автоматизированного проектирования и расчета технологических паpаметpов процесса гибки с растяжением требуют значительных временных затрат (до нескольких часов) на подготовку программы формообразования партии конкретных деталей, что в условиях современного производства неприемлемо. Указанные особенности делают актуальными задачи оперативного программирования в режиме «обучение» для поступившей в производство партии деталей по силам растяжения и последующей своевременной коррекции управляющей программы, воспроизводимой в автоматическом режиме по координатному замыканию.

Рассматривается ориентированная на САПР математическая модель процесса гибки с растяжением, позволяющая повысить эффективность управления формообразованием сложнопрофильных деталей на автоматизированных профилегибочных машинах за счет анализа влияния непрямолинейности свободного участка профиля, который начинается от зоны пластического шарнира и до точки фиксации в зажимном патроне.

Приведены результаты теоретических исследований, в ходе которых проведены модернизация аналитического решения и моделирование гибки с растяжением на основе нового представления о выборе расчетной схемы нагружения, связанной с линией между точкой схода заготовки с пуансона и концом заготовки. При этом растягивающий гидроцилиндр задает величину суммарной силы, приложенной к концу заготовки, а гибочный — направление действия этой силы. За счет использования модели нерастяжимой нити показана принципиальная возможность качественного анализа новых пространственных задач гибки с растяжением в естественных уравнениях равновесия нити на поверхности, в частности, для задачи изготовления сопрягающих профилей между крылом и фюзеляжем самолета.

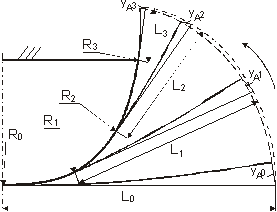
Рис. 2. Сравнение способов формообразования опорной траектории при «старом» и «новом» методах моделирования процесса гибки с растяжением

Предложена новая модель процесса гибки с растяжением, более полно отражающая особенности данной технологической операции (рис. 2). Процесс гибки с растяжением представляется в виде волны деформирования, которая перемещается по длине заготовки вместе с точкой схода с пуансона. После прохождения волны деформированное состояние остается законсервированным. В каждый конкретный момент времени заготовка может быть условно разделена на два участка: первый — уже изогнутый и зафиксированный, и второй, представляющий собой консольную балку, к концу которой приложены силовые воздействия, осуществляющие растяжение и изгиб. Форму первого участка определяет шаблон, для определения формы второго участка используется решение задачи о гибке с растяжением консольной балки с защемленным концом.

Величина y_A — координата точки А — характеризует отклонение траектории перемещения конца реальной заготовки от траектории перемещения нерастяжимой нити той же длины. Выражая y_A через радиус шаблона R_ш в точке схода с него заготовки, учитывая 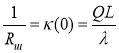, получают:

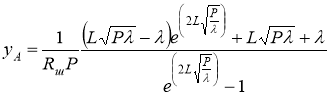,(1)

гдеL — часть длины заготовки, которая еще не коснулась шаблона; — кривизна слоя, проходящего через ось поворота сечения заготовки при изгибе; P и Q — силы растяжения и изгиба, действующие на заготовку;  — параметр, характеризующий свойства материала заготовки и геометрические параметры ее поперечного сечения.

Проведен вычислительный эксперимент по моделированию процесса гибки с (рис.3, 4). Отработана методика использования программного комплекса при расчете напряженно-деформированного состояния формообразуемого профиля.

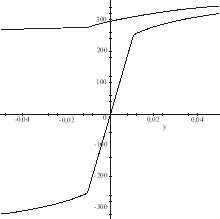
Рис. 3. Распределение напряжений по высоте сечения образца

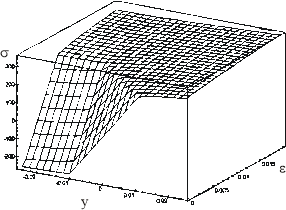
Рис. 4. Распределение напряжений вдоль вертикального сечения образца в зависимости от дополнительного растяжения

Уточненная на основе (1) математическая модель позволила повысить эффективность управления формообразованием сложнопрофильных деталей на автоматизированных профилегибочных машинах.

С учетом проведенных теоретических исследований по уточнению математической модели приведен способ формообразования сложнопрофильных деталей с использованием оперативной коррекции управляющих программ. Проведена модернизация способа формирования координатной сетки контурного управления в режиме «Обучение» по силе растяжения на первой детали. При этом проводится дополнительный учет различных влияющих факторов вида: деформация контура обтяжного пуансона, перераспределение его положения из-за несимметричных нагрузок и др.

Разработан способ формирования координатной сетки автоматизированной профилегибочной машины, заключающийся в том, что первую деталь изготавливают при расчетном изменении гибочного угла по перемещениям, а растяжение заготовки производят по силам с запоминанием приращений перемещений в опорных точках, отличающийся тем, что после исполнения расчетных перемещений гибочного крыла, дополнительно проводят его перемещение до контактирования профиля с концом обтяжного пуансона с одновременным калибровочным растяжным перемещением профиля (рис. 5).

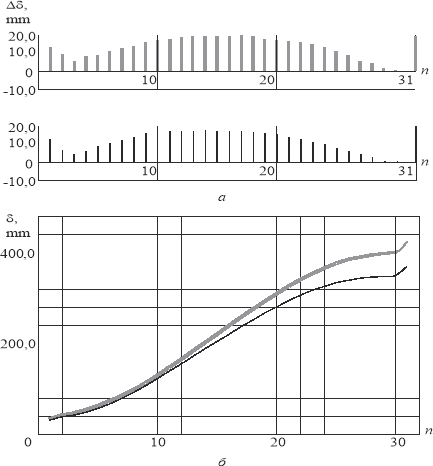
Рис. 5. Сформированные в режиме обучения значения приращений () и перемещений () в реперных точках (n) обобщенной системы координат (угол наклона касательной к контуру пуансона и приращения перемещений) автоматизированной профилегибочной машины

Исследовано влияние на остаточные деформации деталей изменения механических свойств свежезакаленных деталей с течением времени, особенно для случая неудовлетворительной технологической пластичности.

Отработан метод коррекции управляющей программы по критерию точности соответствия контура детали и контура шаблона способом управления по обратной связи (знаковая подналадка), иллюстрирующий повышение точности процесса формообразования на автоматизированных профилегибочных машинах (уменьшение отклонений контура деталей от шаблона до двух-четырех раз, рис. 6).

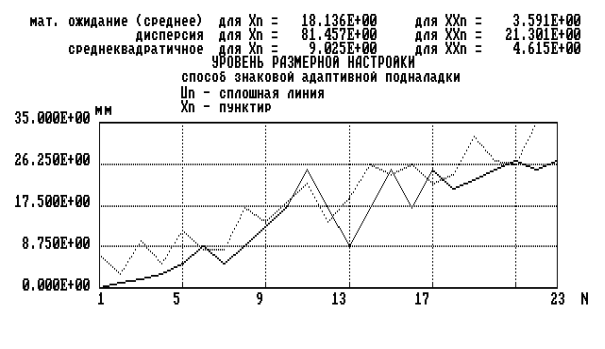
Рис. 6.Знаковая адаптивная подналадка

Отработаны методы определения параметров первоначальной настройки автоматизированной профилегибочной машины с учетом положений фиксации каретки на гибочном крыле, длины заготовки, формы пуансона, диапазона перемещения штока растяжного гидроцилиндра.

Проведено аналитическое и экспериментальное исследование условий закрепления концов профиля в зажимных патронах. Исследовалось влияние ряда возмущений на точность и надежность фиксации заготовки в зажимном патроне. Определены виды нарушений нормального процесса, разработаны рекомендации по их предупреждению. Исследованы аналитически и экспериментально особенности системы «гибочный гидроцилиндр — крыло», определены условия возникновения скоростного замыкания для этой системы, влияющие на качество гибки.

Основные выводы

1. На основе выполненных исследований обосновано управление формообразованием сложнопрофильных деталей на автоматизированных профилегибочных машинах, впервые позволяющее компенсировать влияние криволинейности свободного участка профиля и деформаций обтяжного пуансона при автоматической подготовке и последующей коррекции управляющей программы.
2. С учетом установленной криволинейности свободного участка профиля проведены модернизация аналитического решения и моделирование гибки с растяжением на основе нового представления о выборе расчетной схемы нагружения, связанной с линией между точкой схода заготовки с пуансона и концом заготовки.
3. Разработаны методика и программный комплекс расчета напряженно-деформированного состояния формообразуемого профиля для САПР, позволяющие давать обоснованные рекомендации о выборе технологических схем формообразования на автоматизированных профилегибочных машинах.
4. Проведен вычислительный эксперимент процесса гибки с растяжением. Отработана методика использования программного комплекса при расчете напряженно-деформированного состояния формообразуемого профиля.

Литература:

1. Аналитическое решение задачи гибки с растяжением / А. В. Кочетков, И. Б. Челпанов, В. Б. Гнитько, В. И. Ермолаев // Вестник машиностроения. — 2000, № 7. — С. 46–49.
2. Кочетков А. В., Ермолаев В. И. Классификационные признаки для технологических роботов гибки с растяжением // Исследования станков и инструментов для обработки сложных и точных поверхностей: Межвуз. науч. сб. — Саратов: СГТУ, 2000. -
3. С. 142–144.
4. Бржозовский Б. М., Ермолаев В. И., Карпов А. Н. Совершенствование технологий изготовления трехметровых дорожных реек за счет силового формообразования // Материалы Всерос. науч.-практ. конф. по диагностике автомобильных дорог. — Саратов: ФГУП СНПЦ «Росдортех», 2003. — С. 93–95.
5. Кочетков А. В., Ермолаев В. И., Челпанов И. Б. Проектирование силоизмерительных датчиков, реализуемых на базе штатных деталей машин // Прогрессивные направления развития технологии машиностроения: Межвуз. науч. сб.- Саратов: СГТУ, 2003.- С. 72–76.
6. Малогабаритный пресс для силовых операций с микропроцессорным управлением / Б. М. Бржозовский, С. В. Никаноров, В. И. Ермолаев, А. И. Стекольщиков // Автоматизация и управление в машино- и приборостроении: Межвуз. науч. сб.- Саратов: СГТУ, 2004.- С. 106–108.
7. Ермолаев В. И. Модернизация способа формирования координатной сетки для контурного управления автоматизированной профилегибочной машины в режиме «Обучение» // Автоматизация и управление в машино- и приборостроении: Межвуз. науч. сб.- Саратов: СГТУ, 2004.- С. 53–54.