Учебная компьютерная модель дифракции

Различные способы визуализации количественной информации целесообразно применять тогда, когда невозможно добиться требуемой эффективности обучения при помощи обычного числового представления данных [1; 2; 4; 5]. Идея визуализации данных при обучении не является новой. Однако, несмотря на то, что методы визуализации учебной информации известны достаточно давно, использование научной визуализации в учебном процессе пока только набирает силу. В этом случае, как правило, применяются различного рода манипуляции с получаемыми данными для достижения наибольшей наглядности их представления.

Визуализация направлена на совершенствование техники анализа, но не должна ограничиваться только этим. В некоторых случаях она может вообще замещать сам анализ. Визуализация помогает использовать уникальную способность нашего мозга работать со зрительными образами. Наиболее сложные способы визуализации данных используются для решения естественнонаучных задач [5]. Довольно часто при визуализации информацию сжимают, что позволяет получать различные визуальные представления одной и той же информации. Давно подмечено, что при помощи визуализации можно ознакомиться с информацией, «просто бросив на нее взгляд».

Как уже было сказано, ранее визуализация рассматривалась как вспомогательное средство при анализе данных, сейчас же можно говорить о ее самостоятельной роли в процессе обучения. В своей практике мы используем визуализирующие возможности компьютерной техники для обеспечения необходимой наглядности при изучении полей физических величин (распределений физических величин в пространстве). Итак, при компьютерном моделировании таких распределений с целью их последующей визуализации могут решаться следующие задачи:

-       представление информацию в наглядном виде;

-       компактное описание закономерностей, характерных для исходного набора данных;

-       снижение размерности или сжатие информации.

Применение метода компьютерной визуализации распределений физических величин в пространстве может являться определяющим фактором при формировании понятия поля физической величины [1; 2; 3; 5; 7]. Это позволяет сформировать у учащихся наглядные образы полей физических величин. В связи с этим не обеспечивающие достаточную наглядность традиционные технические средства обучения целесообразно заменить персональным компьютером [3; 5; 6]. Использование вычислительной техники в этом случае вполне естественно, так как решается задача наглядного представления и анализа большого массива числовой информации, полученного в результате измерений или с помощью компьютерного моделирования [3; 6].

Нами разработана серия компьютерных программ, математически моделирующих распределения различных физических величин в пространстве и визуализирующих их [3]. Характер этих распределений позволяет продемонстрировать обучающимся существование тех или иных физических явлений (например, волновых: интерференции и дифракции).

Рассмотрим одну из таких программ, которая демонстрирует обучающимся распределение интенсивности волны, нормально падающей на бесконечно длинную вертикальную щель. Главное окно этого компьютерного приложения показано на рис. 1. Оно содержит схему виртуального опыта и два вида распределений интенсивности волны в пространстве: двумерное (распределение на плоскости, расположенной за щелью) и одномерное (распределение вдоль прямой, расположенной перпендикулярно щели). Первое распределение позволяет дать качественную оценку явлению, второе предоставляет возможность говорить о его количественных характеристиках.

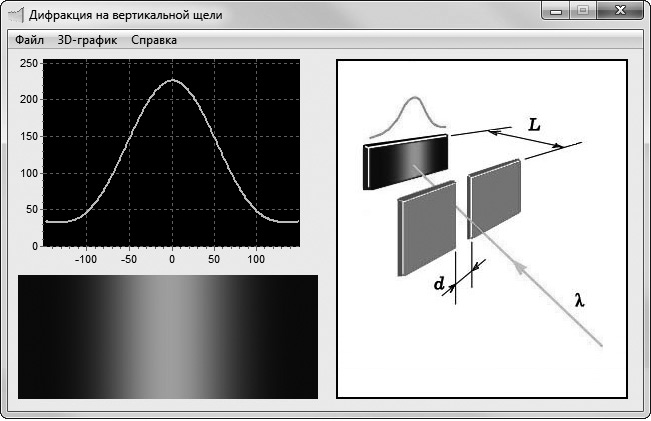
Рис. 1. Окно приложения, моделирующего дифракцию

Программа позволяет продемонстрировать зависимость дифракционной картины от длины волны λ, ширины щели d и расстояния L от щели до дифракционной картины (см. рис. 1). Дидактическая ценность данной программы заключается в том, что она позволяет продемонстрировать различие между приближенными аналитически полученными распределениями и результатами компьютерного моделирования (тоже приближенными, но более точными). Это различие объясняют обучающимся, указывая на то, что аналитически полученные распределения, приводимые в учебниках, соответствуют ситуации, когда расстояние от экрана до дифракционной картины является «очень большим». Программа предоставляет преподавателю возможность продемонстрировать то, что при увеличении этого расстояния картина компьютерного распределения становится все более похожей на картину, полученную аналитически. Предлагаемая нами методика изучения волновых явлений с помощью метода научной визуализации, реализованного посредством компьютерного моделирования, может быть использована при обучении физике в школе и вузе [5].

Литература:

1.   Данилов О. Е. Дидактическая модель формирования понятия поля физической величины с помощью компьютерной визуализации / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 6 (72). — С. 19–28.

2.   Данилов О. Е. Дидактическая модель формирования понятия поля физической величины с помощью компьютерной визуализации на основе таксономии Герлаха-Салливана / О. Е. Данилов // Научно-методический электронный журнал «Концепт». — 2013. — № 3. — URL: http://ekoncept.ru/2013/13053.htm.

3.   Данилов О. Е. Изучение интерференции с помощью компьютерного моделирования / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 9 (75). — С. 50–58.

4.   Данилов О. Е. Компьютерная визуализация распределений физических величин в пространстве / О. Е. Данилов // Молодой ученый. — 2013. — № 11 (58). — Ч. 4. — С. 582–587.

5.   Данилов О. Е. Концепция метода компьютерной визуализации полей физических величин / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 4 (70). — С. 88–97.

6.   Данилов О. Е. Методика изучения интерференции волн от двух точечных источников с помощью компьютерного моделирования / О. Е. Данилов // Молодой ученый. — 2013. — № 2 (49). — Т. 2. — С. 351–358.

7.   Данилов О. Е. Формирование умения проводить теоретическое исследование при изучении распределения физической величины в пространстве с помощью компьютерной модели / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 7 (73). — С. 84–94. /