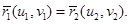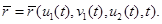Построение линии пересечения двух цилиндров в параметрическом виде

Для производства методом намотки из композиционных материалов элементов трансформируемых конструкций типа тройник, имеющего геометрическую форму двух пересекающихся цилиндров (рис. 1), необходимо иметь математическую модель такого объекта. Важным элементом такой модели является уравнение линии пересечения цилиндров.

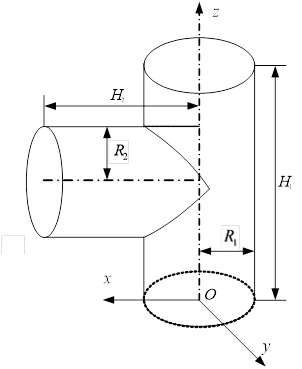
Рис. 1. Линия пересечения двух цилиндров

 

Параметрическое уравнение первого цилиндра (рис. 1) имеет вид:

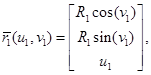                                                                                                 (1)

где 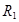 — радиус первого цилиндра.

Параметрическое уравнение второго цилиндра (рис. 1) имеет вид:

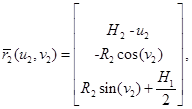
где 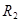 — радиус второго цилиндра,

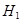 — высота первого цилиндра,

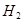 — высота второго цилиндра.

Для заданной конфигурации цилиндров зададим дополнительное условие, ограничивающее радиус второго цилиндра:.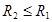

Условие пересечения цилиндров выглядит следующим образом:

В развернутом виде:

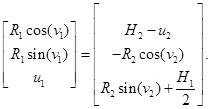                                                                                  (2)

Последняя система уравнений содержит три уравнения и четыре неизвестных величины: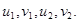

Введем для линии пересечения параметр 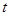, то есть  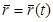— линия пересечения двух цилиндров.

Тогда:

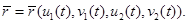                                                                                        (3)

Примем, что 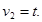 Тогда (3) запишется следующим образом:

Теперь, так как параметр 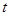 является задаваемой величиной, система (2) зависит от трех переменных:  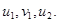C учетом этого перепишем систему (2) следующим образом:

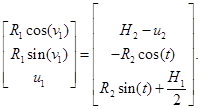                                                                                     (4)

Из третьего уравнения системы (4) имеем:

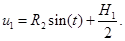                                                                                                        (5)

Из второго уравнения системы (4) имеем:

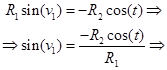
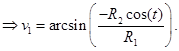                                                                                          (6)

Подставив (5) и (6) в систему (1), получим систему уравнений для линии пересечения цилиндров:

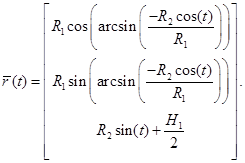                                                                          (7)

Линия пересечения при значении радиусов цилиндров 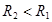 представлена на рисунке 2.

Рис. 2. Линия пересечения цилиндров разного радиуса

 

Первое уравнение системы (7) дает положительные значения координаты X, что позволяем нам задать уравнения линии пересечения в положительном направлении оси X. Для получения уравнения линии пересечения в отрицательном направлении оси X необходимо получить отрицательные значения первого уравнения системы (7).

Воспользуемся тригонометрическими формулами приведения:

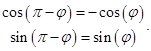
Параметр 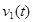 принимает следующий вид:

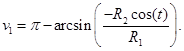
Уравнение для второй линий пересечения принимает вид:

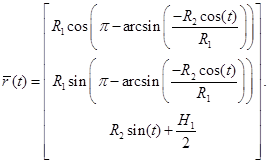
Изображение второй линии пересечения представлено на рисунке 3.

Рис. 3. Вторая линия пересечения

 

Рассмотрим частный случай, в котором значения радиусов цилиндров равны 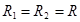. Из второго уравнения системы (4), на основании известных тригонометрических формул приведения, получим:

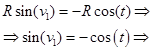
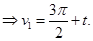                                                                                                                (8)

Из третьего уравнения системы (4) имеем:

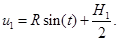                                                                                                         (9)

Подставив (8) и (9) в систему (1), получим уравнение линии пересечения цилиндров (уравнение первого эллипса) равного радиуса:

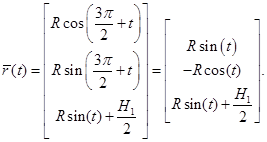                                                                    (10)

Выражение для :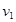

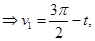                                                                                                               (11)

также является верным, так как с его помощью можно выразить уравнение второго эллипса, по которому пересекаются цилиндры, подставив (9) и (11) в систему (1). Уравнение второй линии пересечения имеет вид:

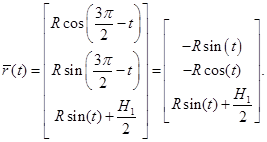                                                                    (12)

Системы уравнений (10) и (12) определяют эллипсы пересечения цилиндров. Для удобства рассмотрения выделим линии пересечения в положительном и отрицательном направлении оси Х через переопределение 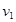 на интервалах  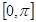и :

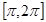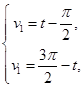
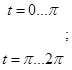                                                                                                                     (13)

Используя для определения 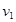 систему (13), можно получить линию пересечения цилиндров равного радиуса в положительном направлении оси Х, а используя систему (14) — в отрицательном.

Линия пересечения цилиндров равного радиуса в положительном направлении оси Х представлена на рисунке 4.

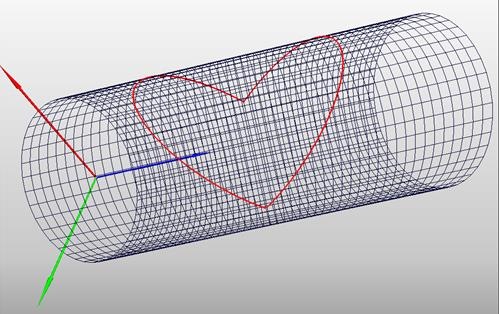
Рис. 4. Линия пересечения цилиндров равного радиуса