Математическая модель волновых явлений в упругом теле при наличии дефектов



В данной работе мы будем считать, что рассматриваемая деталь находится в условиях плоской деформации. Для простоты будем идеализировать изделие в виде прямоугольника. На верхнем участке расположен излучатель. Дефекты представляют собой прямоугольники и . Область на плоскости и , занятую прямыми (т. е. прямоугольник, за вычетом областей и ) обозначим через . Рассматриваемое изделие представляет собой упругое тело с дефектами, которые мы также будем считать упругими телами с характеристиками, отличными от характеристик основного тела. В дальнейшем все величины, относящиеся к горизонтальному включению, будем обозначать индексом «1», а к вертикальному — индексом «2».

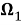
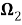
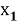
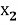
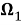
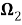
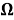
Введём в рассмотрение вектор перемещения упругого тела с компонентами , где

:

(х1, х2, t) = . (1)

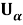
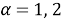
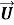
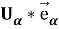
Здесь — орты выбранной системы координат. По повторяющимся индексам подразумевается суммирование.

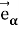
Вектор перемещения удовлетворяет системе уравнений динамической теории упругости с переменными коэффициентами Ляме и :

(2)

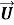
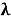
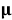
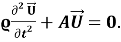
Здесь матричный дифференциальный оператор:

(3)

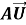
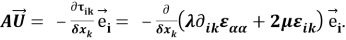
Если и постоянны, то превращаются в обычный оператор теории упругости:

(4)

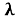
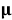
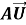
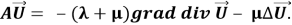
Будем полагать, что коэффициенты упругости рассматриваемого тела являются кусочно-постоянными и могут принимать три значения, для коэффициентов упругости изделия сохраним старые обозначения включений будем обозначать через и . Тогда производные от разрывных функций, фигурирующие в (3), должны быть правильно интерпретированы. Их можно рассматривать в смысле теории обобщённых функций.

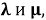
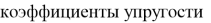
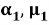
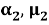
Таким образом, вектор перемещения в областях и удовлетворяет уравнениям:

, (

. (5)

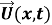
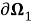
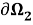
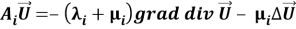
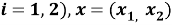
На линиях сопряжения, совпадающие с выполняются условия сопряжения. Они состоят из кинематических условий, означающих непрерывность поля перемещения:

; (6)

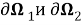
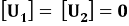
Динамических условий на вертикальных участках :

(7)

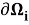
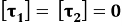
Динамических условий на горизонтальных участках :

(8)

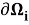
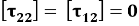
Здесь символом обозначен скачок соответствующей функции при пересечении границы . Напряжение выражается через перемещения следующим образом:

; ; ; (9)

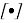
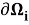
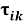
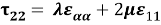
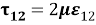
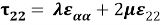
где

.

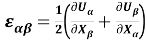
Перейдём к граничным условиям на границе прямоугольника .

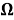
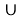
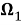
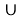
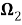
Будем полагать, что при , выполнены условия:

(10)

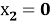
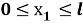
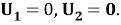
На боковых участках прямоугольника отсутствует напряжение . Это приводит к равенствам:

(11)

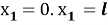
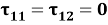
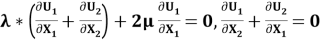
На верхней кромке прямоугольника за исключением участка излучателя, выполняются аналогичные условия:

(12)

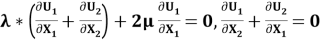
Излучатель развивает некоторое давление. Это приводит к условиям:

(13)

.

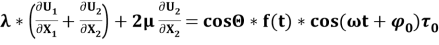
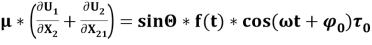
Здесь — некоторый заданный угол: — несущая частота и начальная фаза воздействия, - некоторое характерное давление. Функция огибающую ультразвукового воздействия.

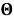
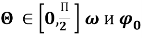
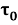
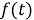
Для завершения формулировки краевой задачи нужно задать начальные условия. Примем их однородными:

(14)

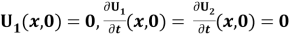
Таким образом, для изучения волнового поля в области нужно решить краевую задачу (5)-(14) Заданными в ней являются величины характеризующие геометрию областей, свойства материала, величины , и функция , описывающие воздействие излучателя. В этом и состоит математическая модель рассматриваемого явления.

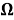
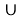
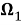
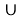
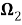
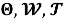
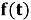
Литература:

1. Викторов И. А. Физические основы применения ультразвуковых волн в технике. — М.; Наука,1966г.
2. Ляв А. Математическая теория упругости. — М.; Наука,1975г.
3. Механика деформируемых твёрдых тел: Направления развития. Сборник статей: Перевод с английского В. В. Шлакова / Под редакцией Г. С. Шапиро. — М.: Мир, 1983г.