Для того, чтобы решить олимпиадную математическую задачу, как и любую другую, нужно, прежде всего, проанализировать текст задачи [1]. Но в случае олимпиадной задачи это может быть затруднительно, поскольку в таких задачах нередко описываются объекты, с которыми невозможно работать. Чтобы разобраться в такой задаче, нужно составить вспомогательную более простую задачу. При этом нужно заменить объект, описанный в задаче, на аналогичный объект, с которым можно экспериментировать. Рассмотрим это на следующем примере.
Задача. Можно ли расставить в клетках прямоугольника 1999×8991 различные натуральные числа так, чтобы каждое число было либо меньше всех чисел, стоящих в соседних по стороне клетках, или больше всех этих чисел?
Для того, чтобы учащиеся включились в решение задачи, они должны начать действовать. Но таблица 1999×8991 настолько велика, что с ней невозможно выполнять реальные действия. В этой ситуации целесообразно составить вспомогательную задачу, решая которую можно провести практическую работу по заполнению таблицы. Можно предложить учащимся следующую вспомогательную задачу: нарисовать таблицу 3×5 и попробовать расставить в ее клетках числа так, чтобы выполнялись условия задачи. Учащиеся, которым это удалось, могут выйти к доске и продемонстрировать свой пример заполнения таблицы. Если же заполнить таблицу не получается, нужно попробовать доказать, что это невозможно сделать.
Выполнение практической работы запускает мыслительный процесс. В результате учащиеся могут найти следующий способ решения задачи: раскрасим клетки таблицы в шахматном порядке. Допустим, получилось 7 белых клеток и 8 черных (рис. 1). Белые клетки заполним числами от 1 до 7 в произвольном порядке, черные — числами от 8 до 15. Таким образом, если число стоит в белой клетке, оно меньше всех чисел, находящихся в соседних по стороне клетках, а если в черной, то больше.
Далее учащиеся должны осознать, что этим способом можно решить задачу с любой таблицей. Если им сложно представить, что клетки таблицы 1999×8991 также можно раскрасить в шахматном порядке и применить к этой таблице тот же метод решения, можно предложить им выполнить еще одну практическую работу, например, с таблицей 4×6. В результате учащиеся осознают, что найденный способ решения можно перенести на задачу с таблицей любого размера, в том числе и 1999×8991.
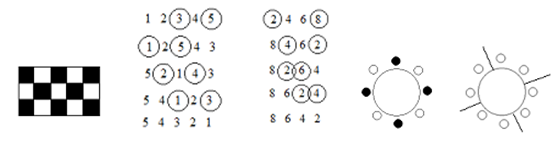
Рис. 1 Рис. 2 Рис. 3 Рис. 4 Рис. 5
Учащиеся смогут овладеть решением олимпиадных математических задач, только если научатся самостоятельно составлять вспомогательные задачи, что требует систематического обучения. Для этого после предъявления основной задачи учитель может предложить учащимся составить вспомогательную задачу, т. е. задачу того же типа, что и основная, но при этом более легкую. Рассмотрим это на следующем примере.
Задача. 100 фишек поставлены в ряд. Разрешается менять местами любые две фишки, стоящие через одну. Можно ли таким способом переставить фишки в обратном порядке? А если фишек 101?
Учащиеся могут составить следующие вспомогательные задачи. В первой задаче могут быть не 100, а всего 3 фишки. Их не сложно переставить в обратном порядке, поменяв местами первую и третью фишки.
В следующей вспомогательной задаче можно рассмотреть 4 фишки. Учащиеся предпринимают попытки переставить их в обратном порядке и убеждаются в том, что это невозможно. В результате они приходят к следующему решению: фишки с четными номерами в результате перестановки могут оказаться только на четных местах, с нечетными номерами — только на нечетных. Поэтому, например, последнюю фишку нельзя поставить на первое место.
В следующей вспомогательной задаче можно рассмотреть 5 фишек. В результате выполнения практической работы учащиеся могут найти, например, такой способ переставить фишки в обратном порядке: поставим сначала пятую фишку на первое место. Это можно сделать за два хода: первым ходом поменяем местами фишки 3 и 5, вторым ходом поменяем местами фишки 1 и 5 (рис. 2). На рисунке в каждой строчке мы обводим кружочками фишки, которые собираемся поменять местами, а ниже пишем строчку после этих изменений. Потом поставим четвертую фишку на второе место и т. д. (последовательность действий видна из рисунка).
В результате учащиеся осознают, что ответ в задаче зависит от того, четное или нечетное количество фишек имеется. В случае четного количества ответ — нет, в случае нечетного — да.
В ходе обучения учащиеся должны осознать, что олимпиадные математические задачи можно разделить на два вида. Первый вид: задача, при изменении числовых данных в которой может получиться только аналогичная задача. Второй вид: задача, при изменении числовых данных в которой может получиться задача другого типа. Рассмотрим пример задачи первого вида.
Задача. На доске написано 100 чисел: 2, 4, 6, …, 200. За один ход можно поменять местами два числа, если одно из них делится на другое. Можно ли с помощью таких действий переставить эти числа в обратном порядке: 200, 198, 196, …, 2?
Практическую работу можно провести с помощью вспомогательной задачи, в которой на доске написано не 100, а всего четыре числа: 2, 4, 6, 8. Переставить эти числа в обратном порядке возможно. Проводя различные пробные попытки, учащиеся могут разработать алгоритм, представленный на рисунке 3.
Выполняя эту практическую работу, учащиеся могут найти общий способ решения таких задач. Для этого нужно заметить, что в этом ряду существует число, которое можно поменять местами с любым числом. Это число 2. Благодаря этому любое число можно поставить на любое место в этом ряду. Поставить число b на место числа а можно в два хода. Первый ход: а меняем местами с 2, второй ход: b меняем местами с 2. Таким образом, переставить числа в обратном порядке можно поставив последнее число на первое место, потом предпоследнее — на второе и т. д.
Если же после выполнения вспомогательной задачи учащиеся не пришли к общему способу решения, учитель может предложить им продолжить выполнять практические работы, теперь с числами: 2, 4, 6, 8, 10.
Таким образом, если мы заменим в основной задаче число 200 на любое другое четное число, мы получим аналогичную задачу, к которой применим найденный общий способ решения. Поэтому это задача первого вида. Рассмотрим теперь пример задачи второго вида.
Задача. Буратино расставляет по кругу целые числа от 1 до 100, а папа Карло дает Буратино по 1 золотому за каждое число, которое больше каждого из своих соседей. Какое наибольшее количество золотых может получить Буратино?
Для проведения практической работы можно рассмотреть вспомогательную задачу, в которой фигурируют числа не от 1 до 100, а например, от 1 до 8. Можно попытаться расставить по кругу числа от 1 до 8 так, чтобы получить как можно больше золотых. В результате пробных попыток учащиеся могут прийти к следующему способу решения: поставим по кругу числа 1, 2, 3, 4 (их обозначают белые кружочки на рисунке 4). Потом в промежутках между ними поставим числа 5, 6, 7, 8 (их обозначают черные кружочки на том же рисунке). За каждое число, обозначенное черным кружочком, Буратино получит по золотому. Значит, он получит 4 золотых.
Докажем, что большего количества золотых Буратино получить не сможет. Разобьем числа, стоящие по кругу, на пары рядом стоящих чисел (рис. 5). Получилось 4 пары. В каждой паре найдется не более одного числа, за которое можно получить золотой, поскольку одно из чисел больше другого. Поэтому больше четырех золотых получить не удастся. Ответ: 4 золотых.
Далее учащиеся должны осознать, что основную задачу можно решить аналогичным образом. В ответе будет: 50 золотых.
В данной задаче в качестве вспомогательных необходимо рассматривать задачи, в которых по кругу нужно расставлять четное число целых чисел. Если взять нечетное число целых чисел, то получится задача уже другого типа. Такую задачу тоже может быть интересно решить, но она сложнее исходной. Поэтому решать ее не обязательно.
Метод вспомогательных задач применим во многих случаях. По мнению психологов, если у человека возникли сложности в решении абстрактной задачи с помощью словесно-логического мышления, целесообразно задействовать наглядно-образное, а в некоторых случаях и наглядно-действенное мышление. Это особый вид мышления, процесс которого сводится к реальным, практическим действиям человека с материальными предметами в наглядно воспринимаемой ситуации [2]. Средством обучения этому могут быть олимпиадные математические задачи.
Литература:
- Подходова, Н. С. Реализация ФГОС ОО: новые решения в обучении математике / Н. С. Подходова, О. А. Кожокарь, Е. Ф. Фефилова. — Архангельск: Изд-во «Кира», 2014. — 255 с.
- Рубинштейн, С. Л. Основы общей психологии / С. Л. Рубинштейн. — М.: Учпедгиз, 1946. — 704 с.

