Рассмотрим решение уравнения

, , (1.1.1)

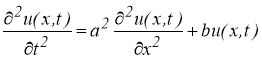
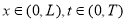
непрерывной в , и удовлетворяющее условиям

, (1.1.2)

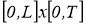
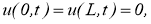
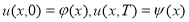
где и непрерывные на [0,L] заданные функции.

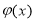
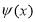
Решим задачу (1.1.1) — (1.1.2) формально, методом разделения переменных (методом Фурье), получим решение в виде ряда:

(1.1.3)

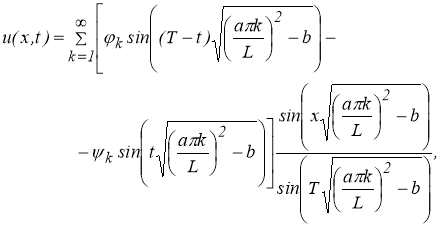
где

,

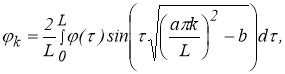
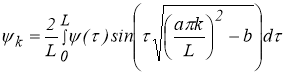
—коэффициенты Фурье функций , соответственно.

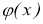
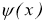
Из выражения для решения (3) следует, что если — рациональное число, то решение в виде ряда либо не существует, либо неединственное, так как существует такое, что . Если — иррациональное число, тогда решение вида (1.1.3) существует, но неустойчиво по отношению к исходными данными, так как при k может быть сколь угодно близким нулю.

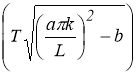
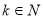
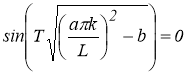
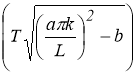
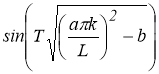
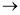
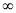
С другой стороне (см. [1,2]), задача суммирования рядов Фурье не обладает свойством устойчивости к малым изменениям в метрике коэффициентов Фурье, если уклонение суммы оценивать в метрике С(0,L) . Следовательно, суммирования ряда (1.1.3), для любого фиксированного не является устойчивым к малым изменениям исходным данным в С(0,L) ( ). Поэтому задачи (1.1.1) — (1.1.2) является некорректно поставленной задачей.

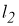
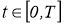
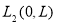
Мы ограничимся рассмотрением задачи (1.1.1) — (1.1.2) при случае, когда — иррациональное число, и, что для точных краевых условий решение в виде ряда (1.1.3) существует.

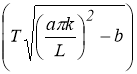
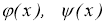
Пусть в (1.1.2) вместо и заданы их приближения и из такие, что

(1.1.4)

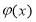
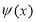
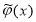
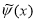
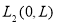
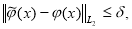
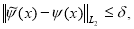
В этих случаях, следуя [2, 3], построим класс устойчивых решений задачи (1.1.1) — (1.1.2). В качестве приближенного решения задачи (1.1.1) — (1.1.2) с приближенными исходными данными будем брать значения однопараметрического семейство операторов вида

(1.1.5)

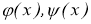
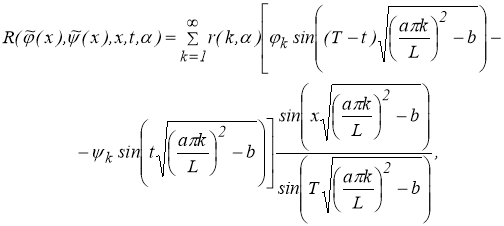
где — коэффициенты Фурье функций по системе на отрезке [0,L] , а r(k, ) стабилизирующие множители, определенные для всех и любых .

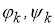
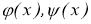
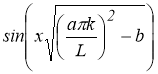
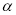
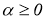
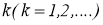
Согласно методу регуляризации [1] и определения 1 и 2 работе [2] надо доказать, что оператор вида (1.1.5) будет регуляризирующим для задачи (1.1.1) — (1.1.2) при подчиняющихся соответствующим условиям стабилизирующих множителях .

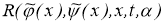
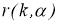
Пусть последовательность удовлетворяет следующим условиям:

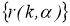
1) для любых значений и k;

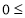
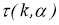
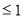
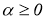
2) ;

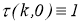
3) для любого последовательность принадлежат пространства ;

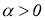
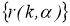
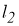
4) для каждого и эта сходимость равномерная относительно где — любое фиксированное положительное число;

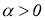
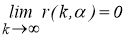
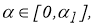
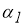
5) для всех k , не убивая;

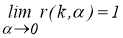
6) для каждого k множитель монотонно убывающая по функция и .

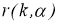
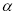
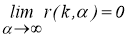
Оценим модуль разности

.

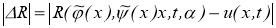
Заметим, что

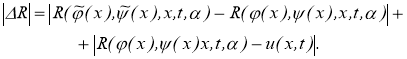
Пусть

,

.

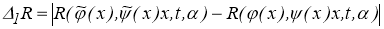
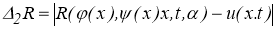
Тогда, из (1.1.5) следует, что

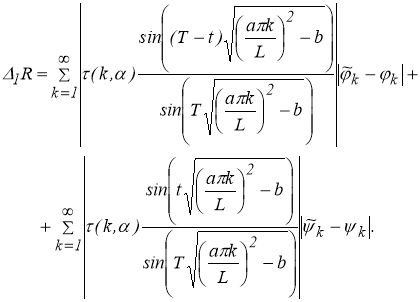
Применяя неравенство Коши — Буняковского [4, 5], получим

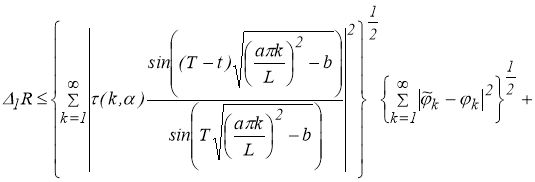
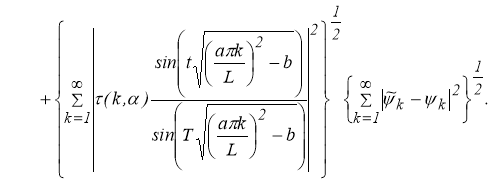
Так как

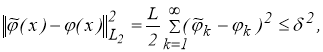
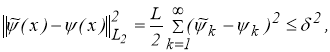
то

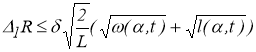
где

,

.

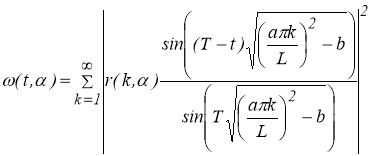
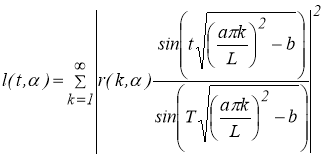
Из (1.1.3) и (1.1.5) следует, что

.

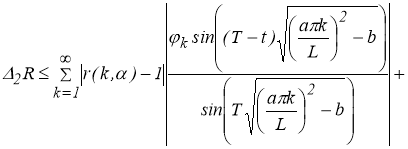
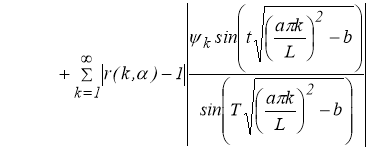
Или

.

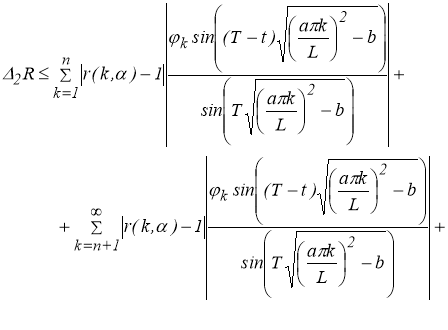
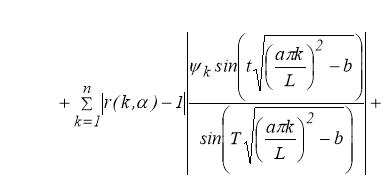
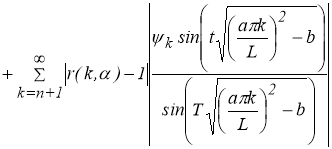
Используя свойство 2, то есть получим

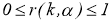
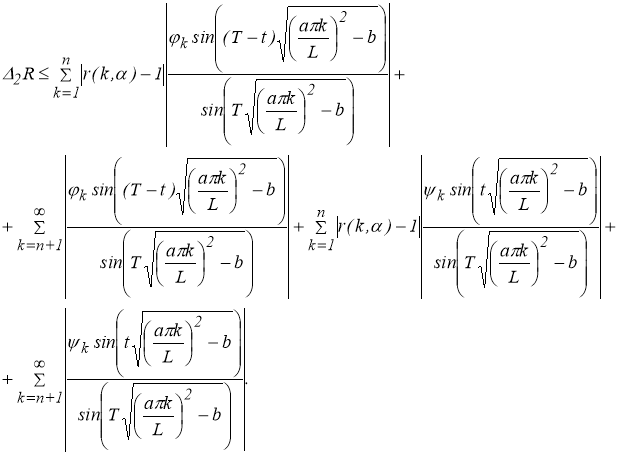
Поскольку для любого фиксированного

и

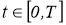
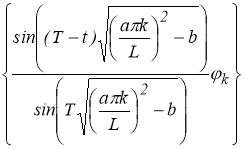
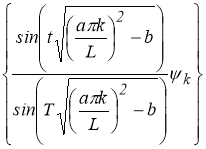
принадлежат (это следует из существования решения в виде ряда (1.1.3)), то для всякого найдется такое , что будет выполняться неравенство

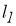
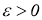
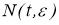
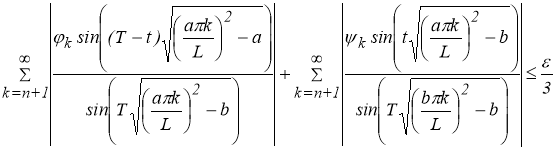
для любых .

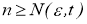
По свойству 6 последовательности найдется такое , что для каждого будет выполняться неравенство

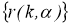
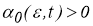
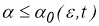
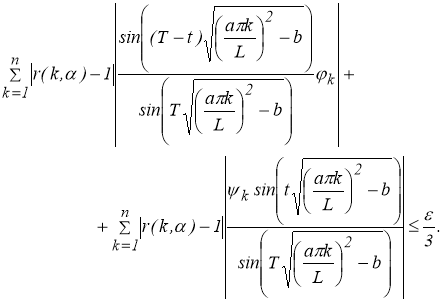
при любом .

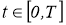
Следовательно,

.

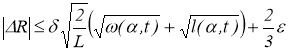
По свойству 6), 7) последовательности для каждого фиксированного ряды и являются убывающими функциями от сходящимися к нулю при .

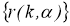
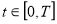
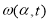
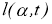
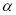
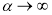
Если

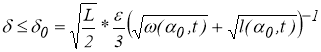
то для всех

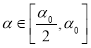
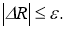
Итак, доказано следующей теоремы.

Теорема 1.1. Если последовательности удовлетворяют условиям 1)-6), то определенный с их помощью оператор вида (1.1.5) является регуляризирующим алгоритмом для задача (1.1.1) — (1.1.2).

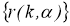
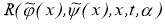
Для наглядной интерпретации полученных результатов используя выраженные (1.1.3) и (1.1.5) проведем численный расчёт зависимости решения задачи (1.1.1) — (1.1.2) от возмущения краевых данных. Результаты расчёта зависимости решения от возмущения краевых данных приведены на рисунке 1. В качестве примера для проведения численных расчётов выбираем алюминиевый сплав AI-Si ( , λ=163,9 Вт/(м2.К ); c _p =0,871 Дж/(кг.К) ; p=2660 (кг/м ³ ) ; ; α=0,0118c; ; L=1; T=0.5; ).

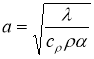
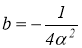
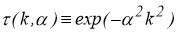
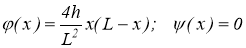
Находим коэффициенты ряда, определяющего решение уравнения (1.1.1): .

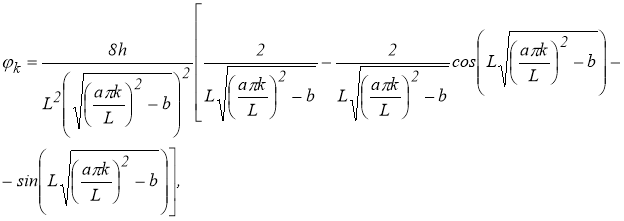
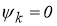
Поэтому решение вида (1.1.3) окончательно принимает вид:

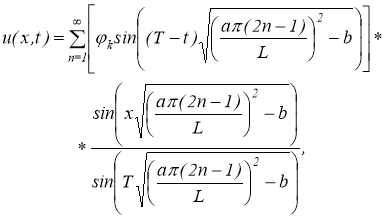
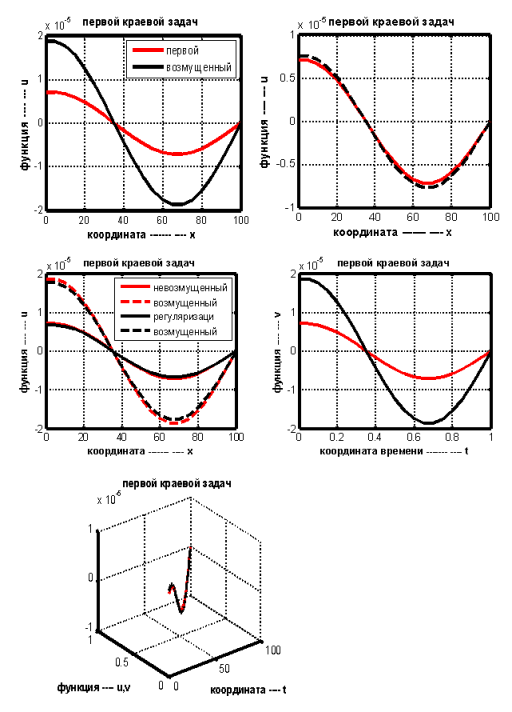
Рис.1. Зависимости решения от исходных краевых данных

Литература:

1. Dzhuraev Kh.Sh. Regularization of Boundary-Value Problems for Hyperbolic Equations / Kh.Sh. Dzhuraev // Mathematical Notes. -2013. –Vol. 93. –No 2. –pp 244–249.
2. Тихонов А. Н., Арсенин В. Я. Методы решения некорректных зачад. -3-е изд. –М.:Наука, 1986. -288с.
3. Джураев Х. Ш., Мелиев Н. Н. Исследование математическое моделей первой краевой задачи для волнового уравнения теплопроводности. / Х. Ш. Джураев, Н. Н. Мелиев // Вестник педагогического университета (Естественных наук). ТГПУ им. С.Айни. 2019.-№ 1–2. –С.115–118.
4. Макаров И. П. Дополнительные главы математического анализа / И. П. Макаров // –М.: Просвещение. -1968. -308с.
5. Колмогоров А. Н. Элементы теории функций и функционального анализа /А. Н. Колмогоров, С. В. Фомин // -М.: Наука. -1981. -544 с.