В настоящее время в обучения физических дисциплин применяются новые педагогические технологии. Например, проблемное обучение, умственное нападение и модельная технология. Какие бы технологии не применялись следует правильно составить математические формулировки физических задач.
При выполнений самостоятельных работ студенты за утрудняются практически строить математический модель рассматриваемой задачи. Для преодоления этих трудностей мы предлагаем простой способ применения математических моделей, для определения сущности физических явлений. Рассмотрим простой пример, пуст тонкая гибкая нить длины l натянута вдоль оси х постоянной силой F. Пусть на нить действует перпендикулярно оси Х сила, распределенная с плотностью f(x). На малой участок нити между точками х и х+dx действует сила f(x)dx, а на всю нить действует сила 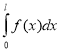 . Найдём форму y=h(x), которую при этом приметь нить.
. Найдём форму y=h(x), которую при этом приметь нить.
Допустим, что приложенная нагрузка имеет специальный вид, а именно, представляет собой единичную сосредоточенную нагрузку, приложенную в некоторой точке воздействия ξ оси х, и обозначим через y=G(x,ξ) соответствующий прогиб в любой точке наблюдения х. Эта функция y=G(x,ξ) называется функцией влияния или функцией Грина рассматриваемой задачи. Можно показать, что если она известно, то легко найти прогиб и от воздействия произвольной нагрузки с плотностью f(x).
Теперь, рассмотрим нагрузку, приходящуюся на участок оси от точки ξ до точки ξ +dξ. Эта нагрузка равен f(ξ)dξ; по этому прогиб от нее в точках равен G(x,ξ)f(ξ)dξ, так как из закона линейности вытекает, что если внешнею нагрузку умножить на постоянный множитель, то и прогиб умножиться на тот же множитель.
Складывая такие бесконечно малые прогибы от всех элементов нагрузки от ξ=0 до ξ=l, получаем суммарный прогиб
![]() (1)
(1)
схемы нагрузок изображены на рис.1.
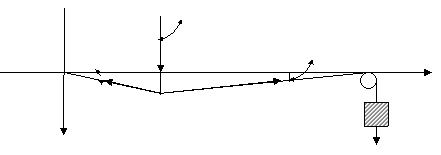
Рис. 1.
В рассматриваемом примере нетрудно выписать функцию G(x,ξ) в явном виде. В самом деле, найдём составляющие сил натяжения нити вдоль оси у слева отточки ξ она равно
![]()
где z-отклонение точки ξ, нам заранее незаданное; отметим, что при этом выводе мы воспользуемся малостью отклонений и поэтому при подсчёте синуса заменили гипотенузу треугольника на его большой катет. Аналогично получаем составляющую силы натяжения с права от ξ
![]()
Если под действием заданной силы нить находится в равновесии, то это означает, что сумма всех сил, действующих на нить, то ее сумма сил натяжения и заданной силы, равна нулю. Поэтому равно нулю и сумма составляющих этих сил по оси у. Так как в нашем случае заданная сила равна 1 и действует вдоль оси у, то на основании предыдущего получаем
![]()
откуда находим
![]()
Если z известно, то отклонение любой точкинити найти легко, пользуясьтем, что нить имеет форму ломанной.
Получим
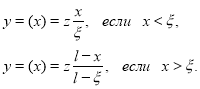
Подставляя сюда найденное значение z и вспоминая, что форма отклонения при единичной сосредоточенной нагрузке даёт функцию Грина, получаем в данной задаче
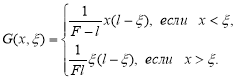
Найденное выражение для функции Грина можно подставить в формулу (1) для прогиба от произвольной нагрузки. Так как ![]() при
при ![]() и при
и при![]() записывается с помощью различных формул, то интеграл разбиваем на два:
записывается с помощью различных формул, то интеграл разбиваем на два:
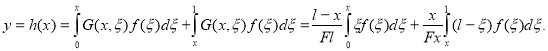 (2)
(2)
Обозначим оператор перехода от функции внешнего воздействия f(x) к функции — «отклику» F(x) через L, так что F=Lf. Мы предположим, имеет место принцип суперпозиции: при сложении внешних воздействия их результаты также складываются, этот закон часто применяется, когда внешние воздействуя не слишком велики.
Теперь, в общем случае мы обозначим через ![]() результат внешнего воздействия, описываемого дельта — функцией с особенностью в некоторой фиксированной точке ξ, тое-с функцией
результат внешнего воздействия, описываемого дельта — функцией с особенностью в некоторой фиксированной точке ξ, тое-с функцией ![]() . Таким образом,
. Таким образом,
![]() (3)
(3)
Как же с помощью этой функции Грина ![]() выразить результат преобразования любой заданной функции f(x)? Для этого представим функцию f в виде суммы «столбчатых» функций, каждая из которых имеет особенность лишь в одной точке ξ, а вне бесконечно малой окрестности этой точки она равна нулю. По этому такая столбчатая функция пропорционально дельта — функции
выразить результат преобразования любой заданной функции f(x)? Для этого представим функцию f в виде суммы «столбчатых» функций, каждая из которых имеет особенность лишь в одной точке ξ, а вне бесконечно малой окрестности этой точки она равна нулю. По этому такая столбчатая функция пропорционально дельта — функции ![]() , а так как интеграл от столбчатой функции равен f(ξ)dξ, то она просто равна
, а так как интеграл от столбчатой функции равен f(ξ)dξ, то она просто равна ![]() . Таким образом, мы получаем представление
. Таким образом, мы получаем представление
![]()
графики столбчатых функции приведены на рис.2
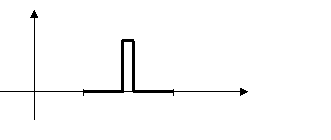
Рис. 2.
Каждую столбчатую функцию можно преобразовать в
![]()
Поэтому сумма таких функций можно преобразовать в
![]()
При бесконечно малых dξ эта сумма является интегралом, т. е. окончательно
![]() (4)
(4)
Функцию влияния можно подсчитать теоретически, как и выше, а более сложных задачах определить экспериментально, произведя необходимые замеры, например, измеряя деформацию системы под действием сосредоточенной силы, могут следовать из общетеоретических принципов. После того как функция Грина найдена и линейность системы установлена, решение задачи пишется по формуле (4) для любого внешнего воздействия f.
Теперь, пользуемся некоторыми представлениями о дельта — функции Дирака δ(х) (Поль Дирак английский физик-теоретик). Возьмем функцию у=ф(х) имеющую максимум при х=0, быстро убывающую в обе стороны от х=0, и притом такую, что
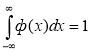
Например,
![]()
Графики этих функций приведены на рисунке 3.
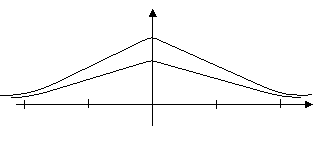
Рис. 3.
Проверим условие дельта — функций
![]() .
.
При помощи δ — функции легко записываются некоторые другие функции, имеющие большое значение. Например, единичная функция
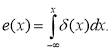 (6)
(6)
Ясно, что при x<0 получаем е(х)=0, а при x>0 получаем е(х)=1. Таким образом, е(х) — это разрывная функция, испытывающая скачок при х=0. Ее график «ступенька» изображен на рис. 4.
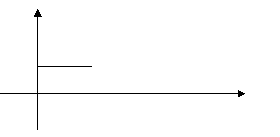
Рис. 4.
Она получается при внезапном подключении какого-либо постоянного воздействия, например, напряжения в электрическую цепь.
Равенство (6) можно получить также с помошью приближённых представлений дельта — функции. Мы видели уже, что одним из таких представлений служит функция ![]() при большом m.Однако
при большом m.Однако
![]()
График этого интеграла при различных m показан на рис. 5.
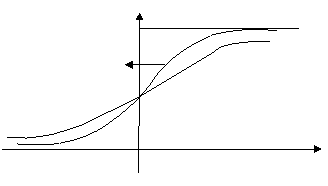
Рис. 5.
Равенство (6) можно продемонстрировать на следующем физическом примере. Рассмотрим прямолинейное движение материальной точки массы m,под действием переменной силы F(t), направленной вдоль этой же прямой. Записав выражение второго закона ньютона и проведя интегрирование, получим равенство
![]()
(принимая, что начальная скорость при ![]() равна нулю). Пусть сила имеет характер удара, т. е.
равна нулю). Пусть сила имеет характер удара, т. е. ![]() . Интегрируя, получим
. Интегрируя, получим
![]()
Это значит, что скорость v равна нулю до удара и равна ![]() после удара.
после удара.
Дельта — функцию можно не только интегрировать, но и дифференцировать; её производная ![]() имеет ещё более «острую» особенность, чем δ(х). Так, если исходить из приближенного представления функции
имеет ещё более «острую» особенность, чем δ(х). Так, если исходить из приближенного представления функции ![]() таком виде при большом m, то мы получаем приближенное представление δ(х) в виде функции
таком виде при большом m, то мы получаем приближенное представление δ(х) в виде функции
![]()
график которой показан на рис. 6.
Рис. 6.
Эта функция принимает экстремальные значения при ![]() равные по абсолютной величине
равные по абсолютной величине ![]() .
.
Эти значения пропорциональны уже m2, а не m, как при представление функцие ![]() .
.
Если ![]() - функция описывает плотность единечного заряда, расположенного в начале координат, то
- функция описывает плотность единечного заряда, расположенного в начале координат, то ![]() описқвает плотность «диполя», расположенного там же. Такой диполь получается если разместить заряды — q и q соответственно в точках х=0 и
описқвает плотность «диполя», расположенного там же. Такой диполь получается если разместить заряды — q и q соответственно в точках х=0 и ![]() , а затем, оставляя
, а затем, оставляя ![]() (момент диполя) без изменения, устремить l к нулю, а q — к бесконечности,так что в пределе получается два равных бесконечно больших заряда противно подложного знака на бесконечно близком расстоянии.
(момент диполя) без изменения, устремить l к нулю, а q — к бесконечности,так что в пределе получается два равных бесконечно больших заряда противно подложного знака на бесконечно близком расстоянии.
До перехода к пределу плотность заряда имеет вид
![]()
Поэтому после перехода пределу при ![]() плотность заряда равно —
плотность заряда равно — ![]() .
.
Литература:
- Фихтенгольц Г. М. Курс дифференциальных и интегральных исчислений. — М., «Наука», 1967.
- Гунтер Р. С., Янпольский А. Дифференциальные уравнения. — М., «Высшая школа», 1980.
- Зельдович Я. Б. Высшая математика для начинающих и ее приложения к физике изд. физмат литературы. — М., 1963.
- Зорич В. А. Математический анализ. Часть 1. — М., «Наука», 1981.
- Самойленко А. М., Кривошея С. А., Перестук Н. А. Дифференциальные уравнения примеры и задачи. — М., «Высшая школа», 1989.

