Для формирования профессиональных компетенций учащихся СПО необходимо владеть рядом учебных дисциплин, имеющих общепрофессиональное значение. Очень важная роль в этом принадлежит математике как универсальному междисциплинарному языку для изучения объектов и процессов. Наряду с формированием предметных знаний и умений у учащихся должны формироваться умения и навыки использования полученных знаний в разнообразных ситуациях, близких к реальным. Одним из основных средств, применение которых создает хорошие условия для достижения данной цели, является решение задач прикладной направленности.
Рассмотрим некоторые примеры решения прикладных задач с применением методов математического анализа.
Задача 1. Города A и B находятся на расстоянии a км и соединены прямой железной дорогой. Для перевозки грузов из города A в город C, отстоящий от железной дороги на b км, необходимо построить автомобильную дорогу, примыкающую к железной дороге (рисунок 1). К какой точке D следует провести шоссе, чтобы транспортировка грузов была наиболее экономичной, если стоимость перевозки 1 тонны груза на 1 км по железной дороге составляет v руб., а по автомобильной дороге — w руб..
Решение. Обозначим через x расстояние от города A до автомобильного съезда D.
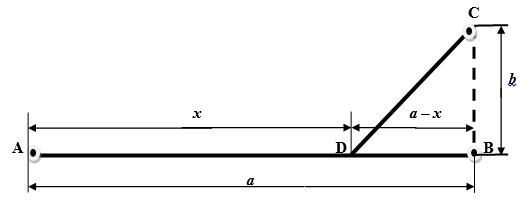
Рис. 1
Отметим, что ![]() . Тогда длина участка ВD = a — x, а длина автомобильного участка СD пути определится по теореме Пифагора и будет равна
. Тогда длина участка ВD = a — x, а длина автомобильного участка СD пути определится по теореме Пифагора и будет равна
![]() . (1)
. (1)
Стоимость перевозки 1 тонны груза по железнодорожному участку AD будет равна ![]() руб., а стоимость перевозки по автомобильному участку СD —
руб., а стоимость перевозки по автомобильному участку СD — ![]() руб.. Следовательно, полная стоимость S транспортировки 1 тонны груза из пункта A в пункт C запишется в виде
руб.. Следовательно, полная стоимость S транспортировки 1 тонны груза из пункта A в пункт C запишется в виде
![]() . (2)
. (2)
Так как полученное выражение для полной стоимости ![]() является функцией расстояния х, то с целью исследования на экстремум найдём её производную
является функцией расстояния х, то с целью исследования на экстремум найдём её производную
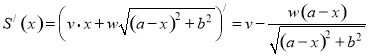 .
.
Из условия равенства нулю производной найдём значение х, в которой функция ![]() достигает экстремума
достигает экстремума
![]()
![]()
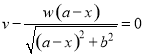
![]()
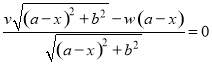
![]()
![]()
![]()
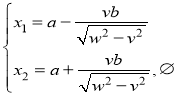 . (3)
. (3)
Очевидно, что значение ![]() не является точкой экстремума, так как не удовлетворяет условию
не является точкой экстремума, так как не удовлетворяет условию ![]() . Следовательно, функция
. Следовательно, функция ![]() достигает экстремума только в точке
достигает экстремума только в точке ![]() . Исследование производной
. Исследование производной ![]() при переходе через точку
при переходе через точку ![]() показало, что в левой окрестности точки
показало, что в левой окрестности точки ![]() производная отрицательна, а в правой окрестности — положительна. Следовательно, в точке
производная отрицательна, а в правой окрестности — положительна. Следовательно, в точке ![]() функция
функция ![]() принимает минимальное значение.
принимает минимальное значение.
Анализ полученных результатов показывает, что полученное решение справедливо лишь при выполнении условия ![]() , то есть если удельные расходы по перевозке грузов по автомобильной дороге (участок CD) будут превышать удельные расходы при транспортировке железнодорожным путём (участок АD). Рассмотрим диапазон возможных значений, в котором может изменяться отношение
, то есть если удельные расходы по перевозке грузов по автомобильной дороге (участок CD) будут превышать удельные расходы при транспортировке железнодорожным путём (участок АD). Рассмотрим диапазон возможных значений, в котором может изменяться отношение ![]() . С этой целью исследуем два предельных случая: 1) х = 0; 2) х = а.
. С этой целью исследуем два предельных случая: 1) х = 0; 2) х = а.
В первом случае, когда х = 0, преобразовав полученное в (3) выражение для ![]() , и приравняв нулю, получим
, и приравняв нулю, получим
![]()
![]()
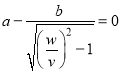
![]()
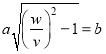
![]()
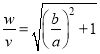 . (4)
. (4)
Это отношение (4) удельных расходов ![]() является минимально возможным, при этом автомобильную дорогу надо строить по прямой АС.
является минимально возможным, при этом автомобильную дорогу надо строить по прямой АС.
Во втором случае, когда х = а, для отношения ![]() будем иметь:
будем иметь:
![]()
![]()
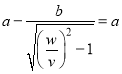
![]()
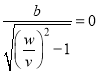
![]()
![]() . (5)
. (5)
Очевидно, что на практике полученное отношение ![]() не может стремиться к бесконечности, а должно иметь конечное значение. Следовательно, оптимальная точка D автомобильного съезда, будет находиться в промежутке
не может стремиться к бесконечности, а должно иметь конечное значение. Следовательно, оптимальная точка D автомобильного съезда, будет находиться в промежутке ![]() .
.
Поставив полученное значение ![]() в (2), найдём минимальное значение полной стоимости транспортировки 1 тонны груза из пункта A в пункт C
в (2), найдём минимальное значение полной стоимости транспортировки 1 тонны груза из пункта A в пункт C
Smin = ![]() . (6)
. (6)
Задача 2. Капля с начальной массой ![]() падает под действием силы тяжести и равномерно испаряется, теряя в единицу времени массу
падает под действием силы тяжести и равномерно испаряется, теряя в единицу времени массу ![]() . Какую работу совершает сила тяжести капли за время падения до полного её испарения?
. Какую работу совершает сила тяжести капли за время падения до полного её испарения?
Решение. Пусть в начальный момент времени (![]() ) масса капли равна
) масса капли равна ![]() , а скорость её испарения равна
, а скорость её испарения равна ![]() . Тогда закон изменения массы
. Тогда закон изменения массы ![]() капли во время движения можно записать в виде
капли во время движения можно записать в виде ![]() . Из условия, что к концу движения капля испаряется полностью, то есть масса
. Из условия, что к концу движения капля испаряется полностью, то есть масса ![]() , найдём время падения
, найдём время падения ![]() до её полного испарения:
до её полного испарения:
![]()
![]()
![]()
![]()
![]() . (7)
. (7)
Во всё время движения ![]() капля совершает свободное падение под действием переменной силы тяжести
капля совершает свободное падение под действием переменной силы тяжести
![]() (8)
(8)
Известно, что если материальная точка движется вдоль оси Ох под действием переменной силы, то работа А силы по перемещению точки из положения ![]() в положение
в положение ![]() равна:
равна:
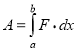 . (9)
. (9)
Так как движение совершается без начальной скорости, то в произвольный момент времени скорость капли определится по формуле ![]() . Тогда за время
. Тогда за время ![]() капля пройдёт расстояние
капля пройдёт расстояние ![]() . Подставив равенство (8) и полученное выражение для
. Подставив равенство (8) и полученное выражение для ![]() в (9), и учтя, что в рассматриваемом случае
в (9), и учтя, что в рассматриваемом случае ![]() и
и ![]() , получим
, получим
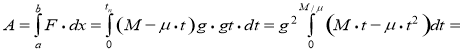
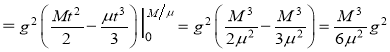 (Дж).
(Дж).
Приведённые примеры показывают важность математической компетенции учащегося, способствующей адекватному применению математики для решения профессиональных задач.
Литература:
- Богомолов Н. В., Самойленко П. И. Математика: учебник для ссузов. — 7 изд., стереотип. — М., 2010. — с. 395.
- Математика. Тренировочные тематические задания повышенной сложности для подготовки к ЕГЭ и к другим формам выпускного и вступительного экзаменов / сост.Г. И. Ковалёва, Т. И. Бузулина, О. Л. Безрукова, Ю. А. Розака — Волгоград: Учитель, 2007. — 494 с.

