Матрицы составляют основной аналитический аппарат для изучения линейных операций в ![]() –мерном пространстве [1]. В свою очередь изучение этих операций дает возможность разбить все матрицы на классы и выявить важные свойства, присущие всем матрицам одного и того же класса.
–мерном пространстве [1]. В свою очередь изучение этих операций дает возможность разбить все матрицы на классы и выявить важные свойства, присущие всем матрицам одного и того же класса.
Известно, что при изучении спектральных свойств блочно-операторных матриц ![]() важную роль играют свойства собственных значений числовых матриц
важную роль играют свойства собственных значений числовых матриц ![]() . Например, при оценке нижней границы блочно-операторных матриц с помощью соответствующей квадратичной числовой образа [2]. С этой целью в настоящей работе изложим некоторые важные свойств таких матриц.
. Например, при оценке нижней границы блочно-операторных матриц с помощью соответствующей квадратичной числовой образа [2]. С этой целью в настоящей работе изложим некоторые важные свойств таких матриц.
Для ![]() рассмотрим матрицу
рассмотрим матрицу
![]() . (1)
. (1)
При исследовании структуры матрицы ![]() большую роль играют векторы
большую роль играют векторы ![]() , для которых
, для которых ![]() . Такие векторы называются собственными векторами, а соответствующие им числа
. Такие векторы называются собственными векторами, а соответствующие им числа ![]() –собственными или характеристическими числами матрицы
–собственными или характеристическими числами матрицы ![]() . Очевидно, что матрица
. Очевидно, что матрица ![]() имеет два собственных чисел с учетом кратности. Собственные векторы, соответствующие различным собственным числам, всегда линейно независимы.
имеет два собственных чисел с учетом кратности. Собственные векторы, соответствующие различным собственным числам, всегда линейно независимы.
Сформулируем основной результат настоящей работы.
Теорема 1.Для собственных чисел ![]() ,
,![]() матрицы
матрицы ![]() имеют места следующие:
имеют места следующие:
(а) Если ![]() и
и ![]() , то
, то
(1.1)![]() ;
;
(1.2)![]() ;
;
(1.3)![]()
(б) Пусть ![]() и
и ![]() . Тогда
. Тогда
(2.1)![]()
(2.2) если ![]() , то
, то ![]() , если при этом
, если при этом
![]() , то
, то ![]() ;
;
(2.3) если ![]() и
и ![]() , то
, то
![]() ,
, 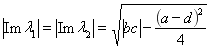 .
.
(в) Если ![]() и
и ![]() , то
, то
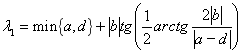 ,
,
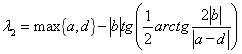 .
.
Доказательство. (а) Пусть ![]() и
и ![]() . Предположим, что
. Предположим, что ![]() (в противном случае рассмотрим
(в противном случае рассмотрим ![]() ) и
) и
![]() (2)
(2)
(в противном случае вместо ![]() берем
берем ![]() ). Из условие (2) вытекает, что
). Из условие (2) вытекает, что
![]() .(3)
.(3)
Собственные значения ![]() удовлетворяет уравнению
удовлетворяет уравнению
![]() .
.
Мы рассмотрим ![]() как функция от
как функция от ![]() и напишем
и напишем
![]() . (4)
. (4)
Разложим вещественные и мнимые части
![]() ;
; ![]() .
.
Возводя на квадрат обе части равенства (4) и приравняв вещественные и мнимые части получим, что ![]() и
и ![]() удовлетворяют соотношение
удовлетворяют соотношение
![]() ;(5)
;(5)
![]() .(6)
.(6)
Последняя уравнение показывает, что собственные значения ![]() лежат в гиперболе с центром
лежат в гиперболе с центром ![]() и асимптотой
и асимптотой ![]() и
и ![]() параллельно к вещественным и мнимым осям. Из тождества (5) следует, что при
параллельно к вещественным и мнимым осям. Из тождества (5) следует, что при ![]() собственные значения
собственные значения ![]() заполняет правый ветвь из
заполняет правый ветвь из ![]() до
до ![]() , а собственные значения
, а собственные значения ![]() заполняет левый ветвь из
заполняет левый ветвь из ![]() до
до ![]() . Отсюда следует утверждение (1.1) и (1.2). Чтобы доказать утверждение (1.3) достаточно показать, что производное гиперболы в точках
. Отсюда следует утверждение (1.1) и (1.2). Чтобы доказать утверждение (1.3) достаточно показать, что производное гиперболы в точках ![]() и
и ![]() по модулю меньше чем
по модулю меньше чем ![]() . Например, для производное в точке
. Например, для производное в точке ![]() из (6) следует, что
из (6) следует, что
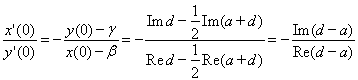 ,
,
которое, в силу (3), по модулю меньше чем ![]() .
.
(б) Доказывается аналогично.
(в) Пусть![]() и
и ![]() . Построим характеристическое уравнение для
. Построим характеристическое уравнение для ![]() .
.
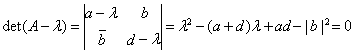
Ясно, что нули этой уравнение, т. е. числа
![]() ;
; ![]() ,
,
являются собственными значениями матрицы ![]() .
.
Используя соотношение ![]() перепишем
перепишем ![]() виде
виде ![]() . Теперь простые вычисления показывают, что
. Теперь простые вычисления показывают, что
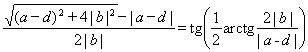 . Таким образом
. Таким образом
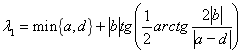 .
.
Совершенно аналогично показывается, что
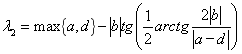 .
.
Теорема 1 доказана.
Литература:
- Ф. Р. Ганхмахер. Теория матриц. — 4-е изд. –М.: Наука, 1988.
- C. Tretter.Spectral theory of block operator matrices and applications. — London:Imperial College Press, 2008.

