О трех различных асимптотах графика одной функции



Из курсов математического анализа и дифференциальной геометрии нам известно, что графики или кривые функций могут иметь три типа асимптот: вертикальные, горизонтальные и наклонные ([1], [2]). Приведен пример функции, зависящей от нескольких параметров, которая также имеет три типа асимптот, и даны условия существования асимптот по параметрам.

Прежде всего, давайте посмотрим на определения асимптот:

Определение 1. Следование заданной функции если хотя бы один из односторонних пределов

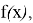
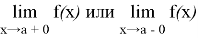
равен +∞ или -∞, то говорят, что график функции имеет вертикальную асимптоту .

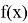
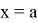
Определение 2. Если

, то прямая называется горизонтальной асимптотой функции.

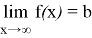
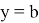
Асимптоты, данные приведенными выше определениями, также называются асимптотами, параллельными осям координат . [3]

Определение 3. Если для заданной функции есть пределы

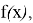
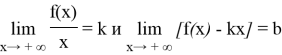
то график имеет асимптоту вида при .

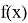
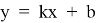
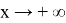
Пример 1. Найдите условия, при которых следующая функция имеет вертикальную и горизонтальную асимптоты.

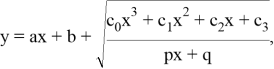
Здесь и не все равны нулю одновременно.

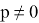
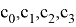
Решение.

1) На основании вышеприведенного определения находим вертикальную асимптоту функции:

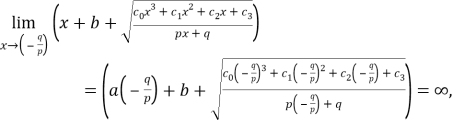
Вот как

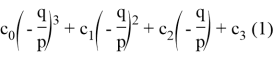
правый или левый пределы выражения равны ∞ или не существуют, в зависимости от знака.

Если (1) значение выражения:

а) если отрицательно, правого предела нет, а левый предел равен ∞;

б) если положительно, то правый предел равен ∞, а левый — нет.

В обоих случаях является вертикальной асимптотой.

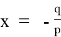
2) Теперь по определению даем горизонтальную асимптоту:

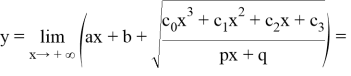
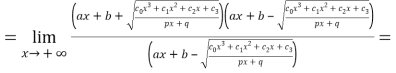
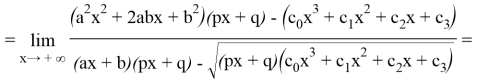
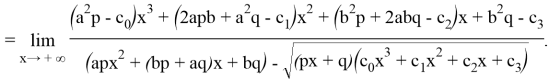
Чтобы эта функция имела горизонтальную асимптоту, . Кроме того, если мы введем условия , это

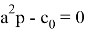
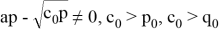
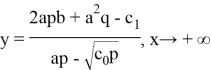
имеем горизонтальную асимптоту.

3) Чтобы найти наклоннию асимптоту функции, найдите предельные значения и , указанные в определение 3:

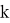
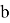
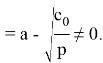
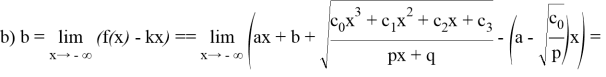
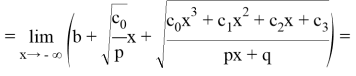
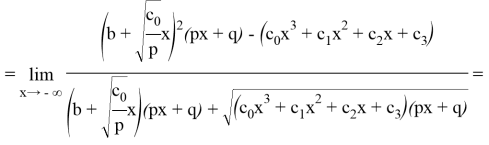
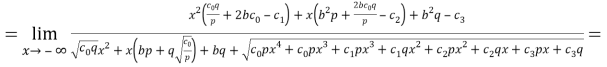
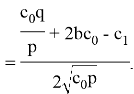
Это означает, что функция имеет наклонную асимптоту

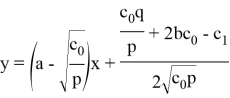
в

условие должно быть выполнено.

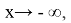
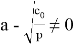
Итак, если объединить вышеуказанные условия, то для того чтобы функция имела все три асимптоты, коэффициенты функции должны удовлетворять следующей системе:

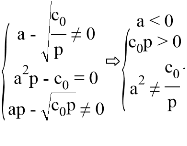
Литература:

1. Sh. Alimov, R. Ashurov — Matematik tahlil. 2-qism. Toshkent: MUMTOZ SO’Z, 2018.

2. Демидович Б. П. Сборник задач и упражнений по математическому анализу Издательство Московского университета Издательство ЧеРо, 1997.

3. Ya. Narmanov, A. S. Sharipov, J. O. Aslonov. Differensial geometriya va topologiya kursidan masalalar to’plami. Toshkent, “Universitet” nashriyoti, 2014.

4. T. Azlarov, H. Mansurov. Matematik analiz: Universitet va pedagogika institutlari uchun darslik: 2 qismli. 1-q.- qayta ishlangan to’ldirilgan 2-nashri. — O’qituvchi, 1994.