В работе изучается задача продолжения решения линейных систем эллиптического типа первого порядка с постоянными коэффициентами в области 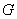 по ее известным значениям
по ее известным значениям 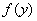 на гладкой части
на гладкой части 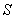 границы
границы 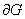 т.е. задача Коши для решения линейных систем эллиптического типа первого порядка с постоянными коэффициентами.
т.е. задача Коши для решения линейных систем эллиптического типа первого порядка с постоянными коэффициентами.
В работе строится семейство вектор функций 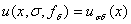 зависящих от параметра
зависящих от параметра 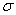 , и доказывается, что при некоторых условиях и специальном выборе параметра
, и доказывается, что при некоторых условиях и специальном выборе параметра 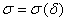 семейство
семейство 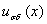 сходится в обычном смысле к решению
сходится в обычном смысле к решению 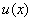 в точке
в точке 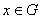 при
при 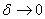 . Семейство
. Семейство 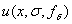 называется регуляризованным решением задачи Коши по М.М. Лаврентьеву.
называется регуляризованным решением задачи Коши по М.М. Лаврентьеву.
Решение задачи Коши для эллиптической системы уравнений Коши-Римана впервые получил Т. Карлеман. Карлеманом была предложена идея введения в интегральную формулу Коши дополнительную функцию, зависящей от положительного числового параметра и позволяющей путем предельного перехода погасить влияние интегралов по части границы, где значения продолжаемой функции не заданы. Идею Карлемана развили Г.М. Голузин и В.И. Крылов, которые нашли общий способ получения формул Карлемана для одномерной системы уравнений Коши-Римана. А.Н. Тихонов показал, что если решение какой–либо некорректной задачи существует и принадлежит компактному подмножеству соответствующего функционального пространства, то из единственности следует устойчивость решения. Вопросы единственности и устойчивости решения задачи Коши для эллиптических уравнений были исследованы Т. Карлеманом, А. Дуглисом , М.М.Лаврентьевым, Е.М. Ландисом, Ш. Ярмухамедовым , Н.Н. Тархановым, А.А. Шлапуновым и др.
Основываясь на результатах Карлемана и Голузина–Крылова, М.М.Лаврентьев ввел важное понятие функции Карлемана для одномерной системы уравнений Коши–Римана и уравнения Лапласа. Функция Карлемана задачи Коши для уравнения Лапласа – это фундаментальное решение, зависящее от положительного числового параметра, стремящегося к нулю вместе со своей производной по нормали на части границы области вне носителя данных Коши, когда параметр стремится к нулю. М.М.Лаврентьев указал способ построения регуляризации некорректной задачи Коши для уравнения Лапласа, если известна функция Карлемана. Функция Карлемана для уравнения Лапласа в явном виде была построена в работе Ш. Ярмухамедова.
Пусть, 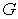 ограниченная область в
ограниченная область в 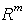 ,граница которой состоит из части плоскости
,граница которой состоит из части плоскости 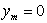 и некоторой гладкой поверхности
и некоторой гладкой поверхности 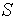 , лежащей в полупространстве
, лежащей в полупространстве 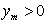 .
.
Пусть, 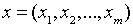 и
и 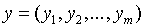 точки т- мерного Евклидового пространства
точки т- мерного Евклидового пространства 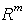 ,
, 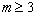 и
и 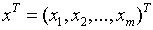 транспонированный вектор х.
транспонированный вектор х.
Введем следующее обозначения:
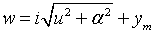 ,
,
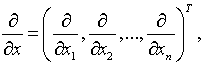
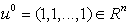 .
.
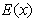 – диагональная матрица,
– диагональная матрица, 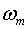 – площадь поверхности единичной сферы
– площадь поверхности единичной сферы 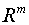 .
.
Через 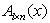 обозначим класс матриц
обозначим класс матриц 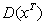 , сэлементами состоящими из линейных форм с постоянными коэффициентами из
, сэлементами состоящими из линейных форм с постоянными коэффициентами из  С которые удовлетворяет условию:
С которые удовлетворяет условию:


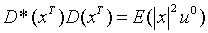
где 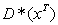 – сопряженная матрица к
– сопряженная матрица к 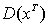 .
.
В области 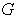 рассмотрим систему дифференциальных уравнений вида:
рассмотрим систему дифференциальных уравнений вида:
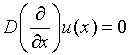 (1)
(1)
где 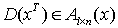
Если 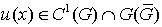 и является решением системы (1), тогда верно следующее интегральное представление:
и является решением системы (1), тогда верно следующее интегральное представление:
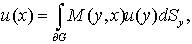
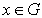 , (2)
, (2)
где
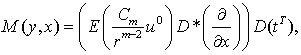
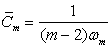
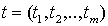 – единичная внешняя нормаль, проведенная в точке
– единичная внешняя нормаль, проведенная в точке 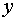 на поверхности
на поверхности 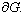
Интегральная формула (2) доказано в работе [1]. Формула (2) также верна, если вместе 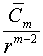 подставим функцию вида:
подставим функцию вида:
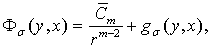 (3)
(3)
где 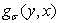 гармоническая функция при
гармоническая функция при 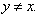
Функция 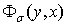 определяется по следующим формулам:
определяется по следующим формулам:
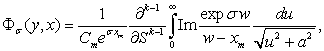
 ,если
,если 
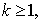 (4)
(4)
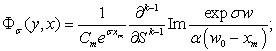
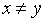 , если
, если 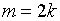
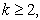 (5)
(5)
где 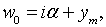
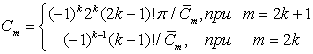
Обозначим
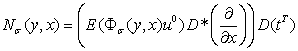 .
.
Тогда интегральная формула имеет вид:
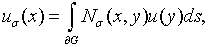
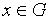 (6)
(6)
Постановка задача. Пусть 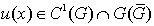 удовлетворяет системе (1) в области
удовлетворяет системе (1) в области 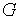 и
и
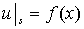 (7)
(7)
Требуется восстановить вектор – функцию в 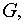 используя данные Коши.
используя данные Коши.
Рассматривается нами задача относятся к некорректно – постановлением задачам, т.е. решение задача неустойчиво. Используя методику проведенную в работе [3], докажем следующее:
Теорема 1.Пусть вектор – функция 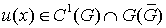 удовлетворяет системе (1), а также граничному условию
удовлетворяет системе (1), а также граничному условию 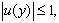 на
на 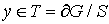 . Если
. Если
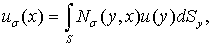
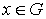 ,
,
то верна следующая оценка:
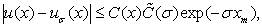
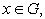 (8)
(8)
где 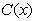 – некоторая функция от
– некоторая функция от  ,
,
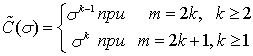
Доказательство. Формулу (6) представим в виде
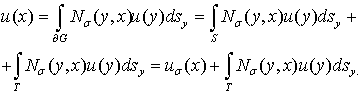
Тогда
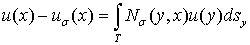
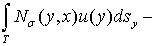 состоит из комбинаций интегралов типа:
состоит из комбинаций интегралов типа:
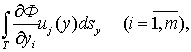
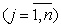 .
.
Следуют оценки интегралов этих типов. Доказательство теоремы сначала приводим в случаи когда 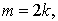
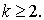
При этом функцию 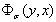 запишем в виде
запишем в виде
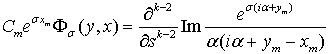
Отделяя мнимую часть функции 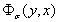 получим:
получим:
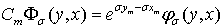 , (9)
, (9)
где
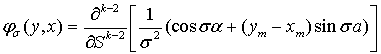 . (10)
. (10)
Используем формулу Лейбница в (10) получим:
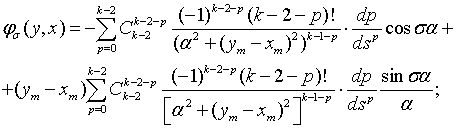 (11)
(11)
где 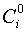 – коэффициенты бинома.
– коэффициенты бинома.
В дальнейшем используем неравенствами при 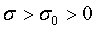 ,
, 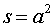
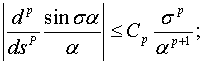 при
при 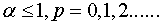
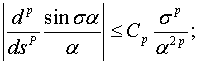 при
при 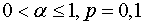
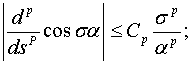 при
при 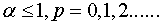 (12)
(12)
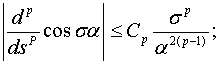 при
при 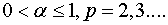
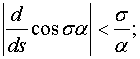
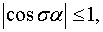 при
при 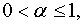
В каждом неравенстве (12) 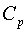 – постоянные различные. В этих неравенствах условие
– постоянные различные. В этих неравенствах условие 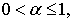 можно заменить условием
можно заменить условием 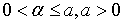 .
.
Оценивая (11) при 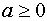 пользуясь неравенствами (12) получим:
пользуясь неравенствами (12) получим:
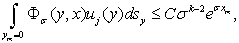
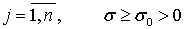
Оценим интегралы типа 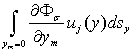 .
.
Для этого находим производную от (11) по 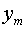 :
:
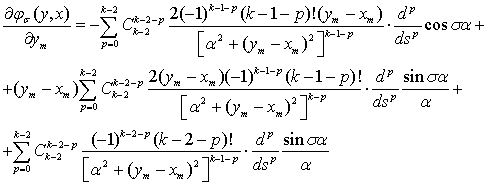 (13)
(13)
Учитывая неравенства (12), из (13) получим следующие оценки:
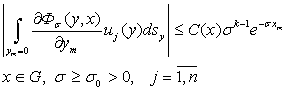 ,
,
Используем следующие формулы:
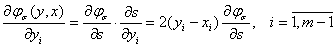 (14)
(14)
Оценим 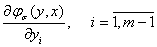 . При этом
. При этом
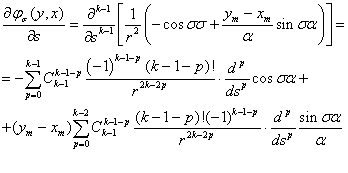 (15)
(15)
Учитывая неравенства (12) и оценивая (15), получим следующее неравенство:
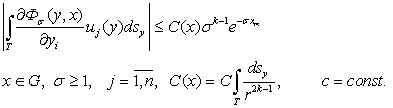
При 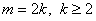 теорема доказано. Теперь теорему докажем при условиях
теорема доказано. Теперь теорему докажем при условиях 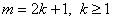 .
.
При этом функции 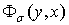 определим из (4), где
определим из (4), где
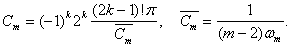
Отделяя мнимую часть функции 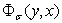 получим:
получим:
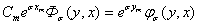 ,
,
где 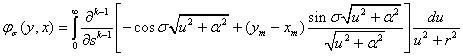 .
.
Теперь функция 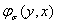 определим следующим образом:
определим следующим образом:
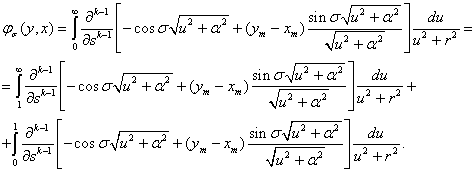 (16)
(16)
Используем неравенства (12) и рассуждая аналогично как в случае четно- мерного пространства, получим из (16) доказательство теоремы.
Следствие 1. Предельное равенство
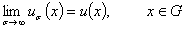
выполняется равномерно в любом компакте из 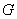 .
.
Пусть 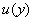 вектор- функция, удовлетворяющая в области
вектор- функция, удовлетворяющая в области 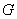 системе (1), и непрерывна в области
системе (1), и непрерывна в области 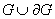 , а также
, а также 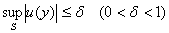 , тогда верно следующее неравенство
, тогда верно следующее неравенство
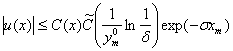
где, 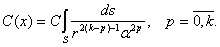
Верна следующая теорема:
Теорема. 2. Пусть вектор функция 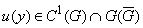 удовлетворяет системе (1),
удовлетворяет системе (1), 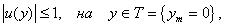
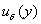 непрерывные приближения
непрерывные приближения 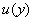 на
на 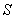 , т.е.
, т.е. 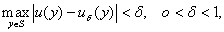
если 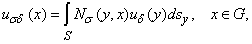 то верно
то верно 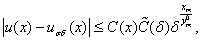
где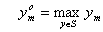 ,
, 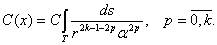
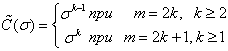 ,
, 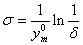
Доказательство. Используем интегральную формулу (6)
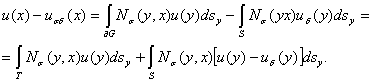
Учитывая утверждение теоремы 1 и неравенства
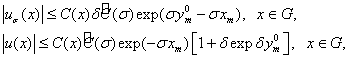
а также полагая 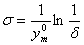 , получим утверждение теоремы 2.
, получим утверждение теоремы 2.
Из этой теоремы следует:
Следствие 2: Предельное равенство
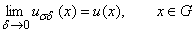
выполняется равномерно на каждом компакте из G.
Литература:
1. Н.Н. Тарханов. Об интегральном представленном решений систем линейных дифференциальной уравнений первого порядка в частных производных и некоторые приложениях. Некоторые вопросы многомерного комплексного анализа. Красноярск –1980, стр. 147- 160.
2. М.М. Лаврентьев. О некоторых некорректных задачах математического физики. Изд. СО АН СССР Новосибирск, 1962 г.
3. Ш.Ярмухамедов. Интегральных представления гармонических функций многих переменных. ДАН СССР, Т.204, № 4, 1972, 799-802 стр.
4. Ш.Ярмухамедов, А. Абдукаримов, З. Маликов. О задачи Коши для системы эллиптического типа первого порядка. Докл. Росс. Акад. Наук. Том 323 (1992) №1.

