Предлагается алгоритм расчета прямоугольных пластин переменной жесткости при различных краевых условиях. Задача сводится к решению систем обыкновенных дифференциальных уравнений четвертого порядка при переменных коэффициентах с помощью метода дифференциальной прогонки. Приведены некоторые численные результаты.
Ключевые слова: дифференциальная прогонка, задача Коши, метод Канторович — Власова, изгиб балки переменного сечения, цилиндрической оболочки переменной толщины, прямоугольной пластинки переменной жесткости.
Вопрос об изгибе прямоугольных пластин переменной толщины — один из сложных в теории изгиба тонких плит. Из-за сложности интегрирования уравнения для прогиба точек срединной поверхности пластинки в настоящее время имеется незначительное число подобных задач, для которых получено точное решение. Поэтому в большинстве случаев такие задачи решаются численными методами.
Эффективность того или иного приближенного метода решения, как известно, определяется многими факторами, среди которых затраты времени на решение задачи и точность полученных результатов являются, по-видимому, наиболее важными.
Анализ широко применяемых приближенных методов приводит к убеждению, что вариационные методы очень трудоемкие в подготовительной работе даже при условии вычисления всех интегралов на компьютере, а метод конечных разностей хотя и универсален, но связен с большим числом алгебраических уравнений.
В данной статье предлагается алгоритм расчета прямоугольных пластин переменной жесткости (толщины) при различных краевых условиях. Задача сводится к решению обыкновенных дифференциальных уравнений четвертого порядка с переменными коэффициентами, которые, в свою очередь сводятся к решению задач Коши.
В качестве исходного возьмем уравнение изгиба пластин переменной жесткости [1], которое в безразмерных координатах будет иметь вид.
,
где
(1)
Здесь переменные с чертой означают переменные в обычных координатах, a-размер пластинки по оси x,b-по оси y,D=D(x,y)-жесткость пластинки, w=w(x,y)- прогиб, q(x,y)-нагрузку (все в безразмерных координатах).
Основные граничные условия дла пластин следующие [1]:
(2)
Комбинируя эти условия, можно получить и другие варианты граничных условий.
Если положить, что жесткость является функцией только переменной х, то из уравнения (I) получим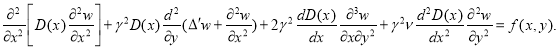 
(3)
Решение уравнения (3) ищем в виде [2]
(4)
где 
-известные координатные функции.
Далее, выполняя процедуры метода Канторовича-Власова, придем к системе обыкновенных дифференциальных уравнений четвертого порядка с переменными коэффициентами:
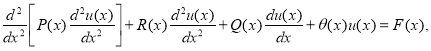(5)
где 
-квадратные матрицы порядка n;
F(x)-n-мерный вектор
Элементы этих матриц и вектора имеют вид
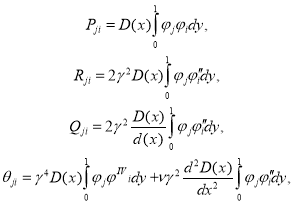
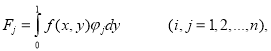
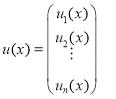
При этом граничные условия (2) принимают форму:
а) для жестко защемленной пластинки-
б) для свободно опёртой –
в) для свободной –
здесь 
и 
-квадратные матрицы вида
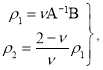(6)
где элементы квадратных матриц А и В определяются как
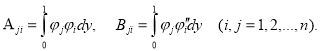
Случай, когда система (5) состоит из одного уравнения, описан в работе [3], где она решается методом дифференциальной прогонки. Аналогично к полученной системе попытаемся применить этот метод.
- Рассмотрим систему (5) при следующих граничных условиях:
(7)
Введя обозначения 
систему (5) приведем к виду
(8)
где
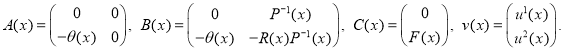
Кроме того, A(x) и B(x) –квадратные матрицы порядка 2n, C(x) и v(x)-2n-мерные векторы.
Граничные условия (7) преобразуется:
v(0)=0, v(1)=0.
Решение системы (8) ищем в виде (9)
с начальными условиями
v(0)=0, (10)
где 
-квадратная матрица порядка 2n;
-мерный вектор.
Для определения
и 
построим систему обыкновенных дифференциальных уравнений
(11)
c начальными условиями
(12)
Таким образом, краевая задача (5), (7) сводится к задачам Коши(11), (12) и (9), (10).
- Если граничные условия для системы (5) представить как
(13)
то решение будем искать в виде(9) и получим систему(11) с начальными условиями(12), а начальными условиями для системы(9) будут
(14)
где 
-квадратные матрицы порядка n(k=2, 4);
β(k)-n-мерные векторы (k=1,2), причем
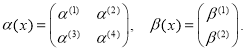
Итак, краевая задача(5), (13) свелась к задачам Коши (11), (12) и (9), (14).
- При граничных условиях для системы (5) типа
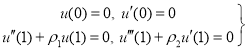(15)
решение будем искать в виде
(16)
где α(x) и β(x)-n-мерные квадратные матрицы;
γ(x)-n-мерный вектор.
Из системы(16) и граничных условий(15) следует, что
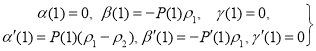(17)
Подставляя(16) в систему(5), приводим к системе обыкновенных дифференциальных уравнений второго порядка с начальными условиями(17) для отыскания α(x), β(x, γ(x):
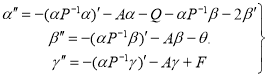, (18)
где 
.
В результате краевая задача(5), (15) сводится к двум задачам Коши-(18), (17) и системе(16) с начальными условиями
.
- Пусть требуется решить системы(5) при граничных условиях
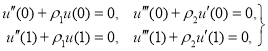(19)
Для удовлетворения первых двух граничных условий(19) систему(16) необходимо решать при следующих начальных условиях:
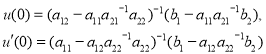
где
- Если систему (5) решать при граничных условиях
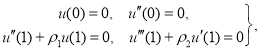
то для системы (16) будем иметь начальные условия
- Рассмотрим систему (5) с граничными условиями
(20)
Решение этой системы ищем в виде
. (21)
Из граничных условий (20) и системы (21) вытекают следующие условия:
(22)
Далее, подставив выражение(21) в систему(5), получим систему обыкновенных дифференциальных уравнений второго порядка для определения неизвестных функций
и 
:
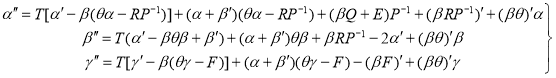(23)
где
.
Начальные условия для системы(21) будут такие:
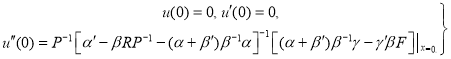(24)
Таким образом, краевая задача(5), (20), сведена к двум задачам Коши: (23), (22) и (21), (24).
Рассмотрим примеры.
Задача 1. Пуст жесткость свободно опертой квадратной пластинки изменяется по закону
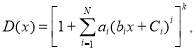
Где k-дейтвительное число, и на пластинку действует сплошная нагрузка интенсивностью f(x).
В этом и других примерах координатные функции выбирались так:
Данная задача при N=k=1, a1=7, b1=1, c1=0, f(x)=1+7x, ν=0, 16 рассмотрена в работах [1,2].
Для сравнения в табл.I приведены численные значения прогиба и изгибающих моментов по оси симметрии
найденные предлагаемым методом, при n=1, где n-число членов ряда(1), и методами, изложенными в работах [1,2,3].
Таблица 1
|
Искомая величина |
Решение |
X |
||||
|
0,175 |
0,335 |
0,494 |
0,653 |
0,812 |
||
|
|
Грань-Ольссона [I] Привед.в в работе [4] Предлагаемым методом |
0,2072 0,2030 0,2069 |
0,3095 0,3085 0,3086 |
0,3270 0,3230 0,3278 |
0,2787 0,2730 0,2782 |
0,1834 0,1700 0,1725 |
|
|
Гран-Ольссона [1] Предлагаемым методом |
0,8676 0,8631 |
1,2683 1,2623 |
1,4778 1,4652 |
1,5116 1,5051 |
1,2277 1,2481 |
|
|
Гран-Ольссона [1] Предлагаемым методом |
0,5935 0,5866 |
1,2171 1,2077 |
1,6630 1,6586 |
1,7613 1,7509 |
1,3965 1,3232 |
Сравнительный анализ показывает хорошее совпадение итоговых данных расчета. Однако метод, предложенный в работе [2], можно применять только в случае, когда жесткость является линейной функцией. В работе же [2] задача сводится к решению бесконечных систем алгебраических уравнений и рассматриваются лишь опертые пластинки, что ограничивает класс решаемых задач.
Предлагаемым методом можно решать задачи практически при любых изменениях функции жесткости. В табл.2 отражены результаты решения задачи I по оси 
при более сложном виде функции жесткости, т. е. при 
Таблица 2
|
Искомая величина |
N |
X |
||
|
0,25 |
0,50 |
0,75 |
||
|
|
1 3 5 |
0,00119 0,00118 0,00118 |
0,00219 0,00217 0,00217 |
0,00221 0,00217 0,00217 |
|
|
1 3 5 7 9 11 |
0,01058 0,01045 0,01050 0,01048 0,01049 0,01049 |
0,01696 0,01669 0,01677 0,01673 0,01675 0,01674 |
0,02095 0,01978 0,02002 0,01994 0,01998 0,01996 |
|
|
1 3 5 7 9 11 |
0,02550 0,02388 0,02418 0,02408 0,02412 0,02410 |
0,02453 0,02219 0,02273 0,02253 0,02264 0,02261 |
0,01305 0,01115 0,01174 0,01150 0,01162 0,01156 |
Для того чтобы показать численную сходимость по методу Канторовича-Власова, в этой таблице представлены данные расчета при различных значениях n, где n- число членов ряда (4) свидетельствующих о довольно хорошей сходимости при этом методе.
Задача 2. Рассчитать прямоугольную пластинку с отношениям сторон 
жесткость которой изменяется по закону
опертую по сторонам у=0 и у=1, защемленную по стороне х=0 и свободную по стороне х=1.
В этом случае граничные условия будут иметь вид
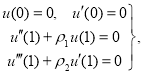
где 
и
вычисляются по формулам (6). Численные результаты для прогиба и изгибающих моментов по оси
и при V=0.25, полученные по методике, описанной в п.3 приведены в табл.3
Таблица 3
|
Искомая величина |
n |
x |
|||
|
0.25 |
0.50 |
0.75 |
1,00 |
||
|
|
1 3 5 |
0,00447 0,00444 0,00444 |
0,00821 0,00817 0,00817 |
0,01050 0,01046 0,01046 |
0,01336 0,01329 0,01329 |
|
|
1 3 5 7 9 11 |
0,00996 0,00956 0,00964 0,00961 0,00962 0,00962 |
0,01369 0,01325 0,01335 0,01331 0,01333 0,01332 |
0,01286 0,01235 0,01246 0,01242 0,01244 0,01243 |
-0,01319 —0,01365 —0,01353 —0,01358 —0,01356 —0,01357 |
|
|
1 3 5 7 9 11 |
0,02234 0,02090 0,02122 0,02110 0,02116 0,02114 |
0,04332 0,04152 0,04191 0,04177 0,04183 0,04180 |
0,05344 0,05131 0,05177 0,05160 0,05168 0,05164 |
0,04617 0,04383 0,04434 0,04416 0,04424 0,04420 |
В заключение необходимо подчеркнуть, что предлагаемый метод позволяет решать довольно широкий класс задач об изгибе прямоугольных пластин как постоянной, так и переменной жесткости. Системы обыкновенных дифференциальных уравнений второго порядка, путем надлежащего введения новых независимых переменных, можно свести к довольно компактным системам обыкновенных дифференциальных уравнений первого порядка, которые легко реализуются на ЭВМ. Кроме того, этот метод с достаточно высокой точностью и при малых затратах машинного времени обеспечивает получение всех необходимых расчетных величин.
Литература:
- М. Олимов, О. О. Жакбаров, Ф. С. Ирискулов, Алгоритм решения прикладных задач для обыкновенных дифференциальных уравнений четвертого порядка с методом дифференциальной прогони, молодой ученыwй, 2015, w6, c.193–196, www.moluch.ru
- Палечек Е. М. Поперечный изгиб прямоугольных пластин переменной жесткости. Труды Калининградского технического института рыбной промышленности и хозяйства, вып 7. Калининградское книжное изд-во, 1963.
- M. Олимов, К. Исманова, П. Каримов, Ш. Исмоилов. Математические пакеты прикладных программ. Тошкент, 2015 г.
